
题目列表(包括答案和解析)
在本章知识应用的过程中,初学者常犯的错误主要表现在:各个概念、现象混淆;对多种可能性的问题分析浅尝则止;计算不过硬。
例1 关于半衰期,以下说法正确的是:
A.同种放射性元素在化合物中的半衰期比单质中长。
B.升高温度可以使半衰期缩短。
C.氡的半衰期为3.8天,若有四个氡原子核,经过7.6天就只剩下一个。
D.氡的半衰期为3.8天,4克氡原子核,经过7.6天就只剩下1克。
[错解]
每经过3.8天就有半数的氡核发生衰变,经过两个半衰期即7.6天后,只剩下四分之一的氡,故选 C,D。
[错解原因]
放射性元素的原子核有半数发生衰变所需要的时间是一种统计规律,半衰期对某一个或某几个原子核来说,是无意义的。“上述”解法忽视了这一事实,故错选了C。
[分析解答]
考虑到放射性元素衰变的快慢是跟原子所处的物理状态或化学状态无关,又考虑到半衰期是一种统计规律,即给定的四个氡核是否马上衰变会受到各种偶然因素的支配。因此,正确答案只有D。

(1)求电子在基态轨道上运动时的动能。
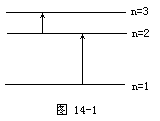
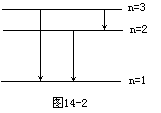
(2)有一群氢原子处于量子数n=3的激发态。画一能级图,在图14-1上用箭头标明这些氢原子能发出哪几条光谱线。
(3)计算这几条光谱线中波长最短的一条的波长。(其中静电力恒量K=9.0×109N·m2/C2,电子电量e=1.6×10-19C,普朗克恒量h=6.63×10-34J·s,真空中光速c=3.0×108m/s)。
[错解]
(1)电子在基态轨道中运动时量子数n=1,其动能为
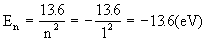
由于动能不为负值
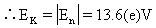
(2)作能级图如图,可能发出两条光谱线。
(3)由于能级差最小的两能级间跃迁产生的光谱线波长越短,所以(E3-E2)时所产生的光谱线为所求,其中
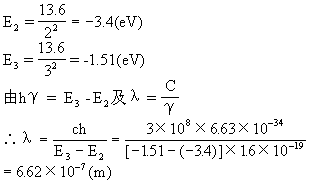
[错解原因]
(1)动能的计算错误主要是不理解能级的能量值的物理意义,因而把
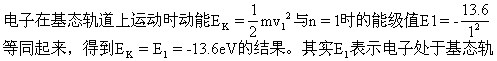
道上的能量,它包括电势能EP1和动能EK1。计算表明EP1=-2EK1,所以E1=EP1+EK1=-EK1,EK1=-E1=l3.6eV。虽然错解中数值表明正确,但理解是错误的。
(2)错解中的图对能级图的基本要求不清楚。
(3)不少学生把能级图上表示能级间能量差的长度线看成与谱线波长成正比了。
[分析解答]
(l)设电子的质量为m,电子在基态轨道上的速率为v1,根据牛顿第

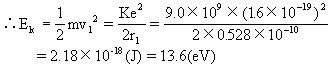
(2)当氢原子从量子数n=3的能级跃迁到较低能级时,可以得到3条光谱线。如图14-2所示。
(3)与波长最短的一条光谱线对应的能级差为E3-E1。
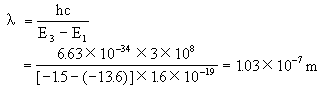
例3 钍232经过6次α衰变和4次β衰变后变成一种稳定的元素。这种元素是什么?它的原子量是多少?它的原子序数是多少?
[错解]

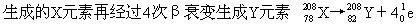
最后生成元素的原子量是208,原子序数是82,由查表知这是铅208,
[错解原因]
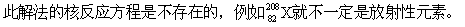
何况反应的次序也不是先进行6次α衰变,再进行4次β衰变,所以此解法是错误的。
[分析解答]
6次α衰变和4次β衰变总的效果使原子量和原子序数变化为
原子量=232-6×4=208
原子序数=90-2×6-4×(-1)=82

本章所涉及的基本方法,由于知识点相对分散要加强物理现象的本质的理解。运用逻辑推理的方法,根据已有的规律和事实、条件作出新的判断。核能的计算对有效数字的要求很高。
本章内容包括α粒子散射、能级、天然放射性现象、α射线、β射线、γ射线、核子、中子、质子、原子核、核能、质量亏损、裂变、链式反应、聚变等,以及原子核式结构模、半衰期、核反应方程、爱因斯坦的质能方程等规律。
10、 变速圆周运动中特殊点的有关问题
l 当汽车以10m/s的速度通过圆拱形桥顶时,车对桥顶的压力为车重的3/4。如果要使汽车在粗糙的桥面行驶至桥顶时不受摩擦力作用,则汽车通过桥顶的速度大小应为 A 15m/s B 20m/s C 25m/s D 30m/s
9、实际运动中向心力来源的分析
8、 用向心力公式解决实际问题
用向心力公式解决实际问题
l 半径为r的圆形转筒绕其竖直中心轴OO’转动,质量为m的物块a在圆筒的内壁上相对圆筒静止,它与圆筒间静摩擦力为Ff,支持力为FN,则下列关系正确的是 A FN=mrω2 B Ff=mrω2 C FN=mg D Ff=mg
7、向心力公式F=mrω2与F=m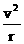 的比较
的比较
l
 压路机后轮的半径是前轮半径的3倍,A、B分别为前轮和后轮边缘上的一点,C为后轮上的一点,它离后轮的距离是后轮半径的一半。则A、B、C三点的向心加速度的比值是
A 9:2:1 B 6:2:1 C
1:2:6 D 2:6:3
压路机后轮的半径是前轮半径的3倍,A、B分别为前轮和后轮边缘上的一点,C为后轮上的一点,它离后轮的距离是后轮半径的一半。则A、B、C三点的向心加速度的比值是
A 9:2:1 B 6:2:1 C
1:2:6 D 2:6:3
6、向心加速度 (1)描述速度方向变化的快慢 (2)加速度的大小和方向
l 一质点以9/πm/s的速率在一个圆形轨道上做匀速圆周运动。若它每经过3s运动方向改变300,则该质点圆周运动的周期为_____s,向心加速度大小为______m/s。
5、向心力
(1)产生加速度的原因
(2)方向:指向圆心,与运动方向垂直
(3)F=man=m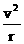 =mrω2
=mrω2
l 一个做匀速圆周运动的物体,如果半径不变,角速度变为原来的3倍,所需的向心力比原来大32N,则物体原来做匀速圆周运动的向心力大小为____N。
4、线速度、角速度、周期和频率之间的关系
v=rω,T=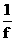 ,v=
,v=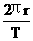 ,ω=
,ω=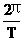 ,ω=2πf
,ω=2πf
l 物体做匀速圆周运动,下列关于它的周期正确的说法是 A 物体的线速度越大,它的周期越小 B 物体的角速度越大,它的周期越小 C 物体的运动半径越大,它的周期越大 D 物体运动的线速度和半径越大,它的周期越小
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com