
题目列表(包括答案和解析)
3.下列说法中正确的是( )
A.1mol的各种物质的质量都相等
B.1mol的氢原子的质量小于1mol氧原子的质量
C.1mol的氢原子数大于1mol的氧原子数
D.1mol任何气体的体积都是22.4L
2.对于液体和固体来说,如果采用M表示摩尔质量,m表示分子质量,ρ表示物质的密度,V表示摩尔体积,v表示分子体积,N表示阿伏加德罗常数,那么反映这些量之间关系的下列各式中正确的是( )
A.N=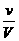 B.N=V/v C.m=M/N D.V=ρM E.
B.N=V/v C.m=M/N D.V=ρM E.
1.酒精和水混合后体积减小的实验表明( )
A.分子间有相互作用力 B.分子间有空隙
C.分子永不停息地运动 D.分子是很微小的
3.估算问题易错
点评 主要原因是不能熟练理解掌握微观量和宏观量以及阿伏加德罗常数的含义及其它们之间的联系,对一些重要的常识性常量如标况下1mol任何气体的体积,水的密度等不能熟记,故而遇到估算问题理不出头绪,仅凭猜测下结论,这样毫无根据的解答,自然易错.
[难题巧解点拨]
例1 已知金刚石的密度是3.5×103kg/m3,试估算碳原子的直径.
解析 碳的摩尔质量M是12×10-3kg/mol,由此可算出碳的摩尔体积为
vm=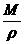 =
=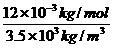 =3.4×10-6m3/mol.
=3.4×10-6m3/mol.
碳原子体积为:
v=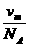 =
=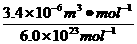 =5.7×10-30m3.
=5.7×10-30m3.
把碳原子看作是小立方体,那么碳原子的直径为
d=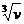 =
=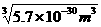 =1.8×10-10m.
=1.8×10-10m.
例2 铁的密度是7.8×103kg/m3,有一小块铁的体积是5.7×10-8m3,这块铁中含有多少个原子?
解析 铁的摩尔质量为55.85×10-3kg/mol,这一小块铁的质量为
m=ρv=7.8×103×5.7×10-8kg=4.4×10-4kg.
它相当的摩尔数为
n=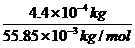 =7.9×10-3mol.
=7.9×10-3mol.
含有的原子个数为:
n′=7.9×10-3mol×6.0×1023mol-1=4.7×1021
例3 从下列哪一组数据可以算出阿伏加德罗常数?( )
A.水的密度和水的摩尔质量 B.水的摩尔质量和水分子的体积
C.水分子的体积和水分子的质量 D.水分子的质量和水的摩尔质量
解析 本题主要考查阿伏加德罗常数表示的物理意义,阿氏常数是指1mol的任何物质中含有的粒子数,显然在四个选项中只有水分子的质量和水的摩尔质量可以算出阿氏常数.
答案 选D.
例4 已知铜的摩尔质量M=63.5g/mol,铜的密度是ρ=8.9g/cm3,试估算铜原子的质量和铜原子的体积.已知NA=6.02×1023mol-1.
解析 设想铜原子是一个个紧挨着排列的,利用阿伏加德罗常数即得.
铜原子的质量:
m=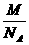 =
=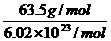 =1.06×10-22g.
=1.06×10-22g.
铜原子的体积:
v=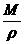 ·
·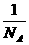 =
=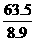 ×
× cm3=1.2×10-23cm3.
cm3=1.2×10-23cm3.
例5 由油滴实验测得油酸分子的直径为1.12×10-9m,已知油酸的密度为6.37×102kg/m3.油酸的摩尔质量为282g/mol,试求阿伏加德罗常数.
解析 设想油酸分子一个挨一个排列,1mol油酸分子的质量为M,密度为ρ,油酸分子的直径为d,把每个油酸分子当作弹性小球,则其体积为v=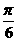 d3,1mol油酸的体积为v=
d3,1mol油酸的体积为v=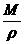 ,1mol油酸所含的微粒数,即阿伏加德罗常数为NA,则
,1mol油酸所含的微粒数,即阿伏加德罗常数为NA,则
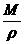 ·
·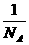 =
=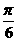 ·d3
·d3
代入数据得NA=6×1023mol-1.
[命题趋势分析]
本节主要考查摩尔质量、分子质量和阿伏加德罗常数之间的关系以及分子(原子)的大小以及分子之间的距离的估算.
[典型热点考题]
例 已知铜的密度为8.9×103kg/m3,相对原子质量为64,质子和中子的质量均约为1.67×10-27kg,则铜块中平均每个铜原子所占的空间体积约为 m3.
解析一
由 v=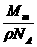 =
=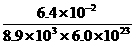 m3=1.2×10-29m3.
m3=1.2×10-29m3.
解析二
取Vm体积铜,则质量m=ρVm.每个铜原子质量m=64×1.67×10-27kg ∴Vm的铜中分子数N=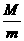 .
.
故平均每个铜原子所占空间体积
V=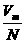 =
=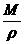 =
=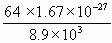 m3=1.2×10-29m3.
m3=1.2×10-29m3.
说明 a.解法1套用现成公式,利用了阿伏加德罗常数,而未用题给质子、中子质量,作为估算是可以的;b.解法2紧扣题中所给量,未用阿伏加德罗常数,也可取定M质量的铜为对象求解,也导出V=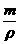 .
.

[同步达纲练习]
2.单分子油膜法实验中,计算油滴体积容易出错
点评 本教材做单分子油膜实验,取材油酸酒精溶液,将配制好的油酸溶液取一滴滴到水面上,随着酒精溶于水,其中的油酸在水面上便形成单分子油膜,这里不少学生容易将滴到水面上油酸酒精溶液的体积当作油膜体积.
1.错将气体分子间距立方体当作气体分子立方体模型
点评 气体分子间空隙很大,气体分子间距比气体分子直径大很多,气体分子间距立方体比分子立方体大很多,二者不能混为一谈,对气体而言,公式v=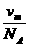 =
=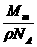 是分子间距立方体体积,而并非分子体积.
是分子间距立方体体积,而并非分子体积.
2.阿伏加德罗常数
(1)阿伏加德罗常数的含义是:1摩尔的任何物质含有的微粒数相同,这个数叫阿伏加德罗常数.其值是6.02×1023mol-1,粗略计算可取6.0×1023mol-1.这个数常用NA表示,是微观世界的一个重要常数,是联系微观世界和宏观世界的桥梁.
(2)能够用来进行四个方面的计算:
1)已知液体和固体的摩尔体积vmol和一个分子的体积v,求NA,则NA=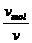 ;反之亦可估算分子的大小.
;反之亦可估算分子的大小.
2)已知物质的摩尔质量M和一个分子的质量m,求NA=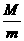 ;反之亦可估算分子的质量.
;反之亦可估算分子的质量.
3)已知物质的体积v和摩尔体积vmol,求物质的分子数n,则n=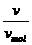 NA=
NA=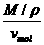 NA.其中ρ是物质的密度,M是物质的质量.
NA.其中ρ是物质的密度,M是物质的质量.
4)已知物质的质量和摩尔质量,求物质的分子数,则n=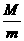 NA.
NA.
[重点难点解析]
重点 阿伏加德罗常数及应用.
难点 摩尔质量、摩尔体积与分子质量、分子体积的联系.
1.分子的大小和质量
(1)把分子看作是一个弹性小球,这是分子动理论中对分子的简化模型,对于分子来说,根据问题的需要,可以有不同的模型,在不涉及分子的内部结构和运动时,可以用小球作为分子的模型,例如在计算液体、固体分子直径时,还经常认为这些小球是紧密排列的,实际上,分子不仅不是真的球体,而且分子之间也有空隙,我们计算出的分子直径和大小只是一个粗略的数量级,或者说是一种估算值.
(2)用油膜法测分子直径的实验,能够说明分子的大小、公式d=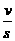 中,v是油滴的体积,s是水面上形成单分子油膜的面积.
中,v是油滴的体积,s是水面上形成单分子油膜的面积.
(3)记住二个数值:分子直径的数量级是10-10m;一般分子质量的数量级是10-26kg.
11、根据打点的纸带判断纸带的运动性质:等间距--匀速直线运动;不等间距--变速直线运动
l 电磁打点计时器使用的电源是: A 4V~6V的交流电源 B 4V~6V的直流电源 C 220V的交流电源 D 高压直流电源
l 用打点计时器研究纸带的运动规律时,在拉动纸带和合上电源开关两个操作中,应当先进行的操作时 A 先拉动纸带 B 先合上开关 C 拉动纸带和合上开关同时进行 D 先进行哪个操作都可以
l 在用电磁打点计时器作测定变速直线运动的平均速度实验时,除了打点计时器、纸带、铅笔,还需要的器材是:__________________。
l
 图示为某次实验打出的纸带,电源的频率为50Hz,由图可知,A、B两点对应的时间间隔为_______s,纸带运动在A-〉B的路程上的平均速度为_______m/s。
图示为某次实验打出的纸带,电源的频率为50Hz,由图可知,A、B两点对应的时间间隔为_______s,纸带运动在A-〉B的路程上的平均速度为_______m/s。
10、根据计数点间的间距计算平均速度
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com