1、在一种叫"蹦极跳"的运动中，质量为m的游戏者，身系一根长为L，弹性优良的轻质柔软橡皮绳，从高处由静止开始下落1.5L时到达最低点，若在下落过程中不计空气阻力，则下列说法正确的是　 A．速度先增大后减小B.加速度先增大后减小C．动能增加了mgL D.重力势能减小了mgL

2、设撤去力F前物块的位移为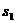，撤去力F时物块速度为，物块受到的滑动摩擦力

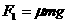　　 对撤去力F后物块滑动过程应用动量定理得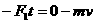

由运动学公式得　　 对物块运动的全过程应用动能定理

由以上各式得　　 代入数据解得F=15N

2、(1)设水平向右为正方向，有：I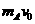＝　　　　　 　　　　　　　　 ①

代入数据得：v=3.0m/s　　　　　　　　　　　　　　 ②

(2)设A对B、B对A、C对A的滑动摩擦力的大小分别为、、，B在A上滑行的时间为t，B离开A时A和B的速度分别为和，有

　　　　　　　　　　　　　　　　　　　　　　　　 ③

　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　④

其中＝

　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑤

设A、B相对于C的位移大小分别为s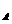和s，有

　　　　　　　　　　　　　　　　　　　 ⑥

　s＝　　　　　　　　　　　　　　 ⑦

动量和动能之间的关系为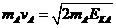：　　　　　　　　　　　　　　 ⑧

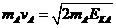　　　　　　　　　　　　　　 ⑨

木板A的长度　L＝s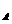－s　　　　　　　　　　　⑩

代入数据得：L=0.50m　　　　　

(10月16日)、1、(1)设人的质量为m，在星球表面附近的重力等于万有引力，有

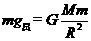　　　　　　　　　　　　　　　　　 ①

　　解得　　　　　　　　 ②

　 (2)设人能上升的最大高度为h，由功能关系得

　　　　 　　　　　　　　　　　　　③

　　　 解得　h＝　　　　　　　　　　　　　　　 ④

2、解：(1)由mgR＝+得

　　　β＝3

(2)设A、B碰撞后的速度分别为v₁、v₂，则

　设向右为正、向左为负，解得

　　　v₁＝，方向向左

v₂＝，方向向右

设轨道对B球的支持力为N，B球对轨道的压力为N ^/，方向竖直向上为正、向下为负。则　

N－βmg＝

　　　N ^/＝－N＝－4.5mg，方向竖直向下

(3)设A、B球第二次碰撞刚结束时的速度分别为V₁、V₂，则

解得：V₁＝－，V₂＝0(另一组：V₁＝－v₁，V₂＝－v₂，不合题意，舍去)

由此可得：

当n为奇数时，小球A、B在第n次碰撞刚结束时的速度分别与第一次碰撞刚结束时相同

当n为偶数时，小球A、B在第n次碰撞刚结束时的速度分别与第二次碰撞刚结束时相同

(10月15日)、1、1)由碰撞过程动量守恒Mv₁=(M+m)v₂　　 ①

　　　　 则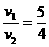

　 (2)设卡车刹车前速度为v₀，轮胎与雪地之间的动摩擦因数为μ两车相撞前卡车动能变化　 　　　　　　②

　　　　 碰撞后两车共同向前滑动，动能变化

　　　　 　　　　③

　　　　 由②式

　　　　 由③式

　　　　　 又因

　　　　 如果卡车滑到故障车前就停止，由　 ④

　　　　 故

　　　 　　这意味着卡车司机在距故障车至少L处紧急刹车，事故就能够免于发生。

2、(1)运动员从D点飞出时的速度 v=

依题意，下滑到助滑雪道末端B点的速度大小是30 m/s

(2)在下滑过程中机械能守恒，有

　mgh=

下降的高度　　　　　　 h=

　(3)根据能量关系，有mgh-W_t=

运动员克服阻力做功W_t=mgH－=3 000 J

(10月14日)、1、(1)由机械能守恒定律得，有

　　　　　　　　　　①

　　　　　　　　②

(2)A、B在碰撞过程中内力远大于外力，由动量守恒，有

　　　　　　　③

　　A、B克服摩擦力所做的功

W＝　　　　　　　④

由能量守恒定律，有

　　　 ⑤

解得

　　　　⑥

2、(1)根据机械能守恒　 E_k=mgR

(2)根据机械能守恒　 ΔE_k=ΔE_p

mv²=mgR

小球速度大小　v=

速度方向沿圆弧的切线向下，与竖直方向成30°

(3)根据牛顿运动定律及机械能守恒，在B点

N_B－mg=m　,mgR＝mv_B²

解得　 N_B=3mg

在C点：N_C=mg

(10月13日)、1、设小物块的质量为m，过A处时的速度为v，由A到D经历的时间为t，有

　　　　　　　　　 ①

　　　　2R＝gt² ②

 s＝vt　　　　　　　　　　 ③

由①②③式并代入数据得

　　s＝1m　　　　　　　　　　 ④

评分参考：①②③④式各4分。

2、解：由于连结AB绳子在运动过程中未松，故AB有一样的速度大小，对AB系统，由功能关系有：

Fh－W－m_Bgh=(m_A+m_B)v²

求得：W=Fh－m_Bgh－(m_A+m_B)v²

(10月12日)、1、解：设分离前男女演员在秋千最低点B 的速度为v₀，由机械能守恒定律

(m₁+m₂)gR=(m₁+m₂)v₀²

设刚分离时男演员速度的大小为v₁,方向与v₀相同；女演员速度的大小为v₂，方向与v₀相反，由动量守恒，　(m₁+m₂)v₀=m₁v₁－m₂v₂

分离后，男演员做平抛运动，设男演员从被推出到落在C点所需的时间为t ，根据题给条件，由运动学规律，　4R=gt²　　 s=v₁t

根据题给条件，女演员刚好回到A点，由机械能守恒定律,　m₂gR=m₂v₂²

已知=2,由以上各式可得　 s=8R

2、匀减速运动过程中，有：

　　　　　　　(1)

恰好作圆周运动时物体在最高点B满足： mg=m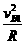　　 　＝2m/s　　(2)

　假设物体能到达圆环的最高点B，由机械能守恒：　 　　(3)

　 联立(1)、(3)可得　 =3m/s

　因为＞，所以小球能通过最高点B。

　小球从B点作平抛运动，有： 2R＝　(4)　　　 　(5)

由(4)、(5)得： ＝1.2m　　　　 (6)

(10月11日)、1、开始时，A、B 静止，设弹簧压缩量为x₁，有kx₁=m₁g　 ①

挂C并释放后，C向下运动，A 向上运动，设B刚要离地时弹簧伸长量为x₂，有kx₂=m₂g　　 ②B不再上升，表示此时A 和C的速度为零，C已降到其最低点。由机械能守恒，与初始状态相比，弹簧弹性势能的增加量为

ΔE＝m₃g(x₁+x₂)－m₁g(x₁+x₂)　 ③

C换成D后，当B刚离地时弹簧势能的增量与前一次相同，由能量关系得

(m₃+m₁)v²+m₁v²=(m₃+m₁)g(x₁+x₂)－m₁g(x₁+x₂)－ΔE　　 ④

由③ ④ 式得(m₃+2m₁)v²=m₁g(x₁+x₂)　　 ⑤

由①②⑤式得v=　　⑥

2、质量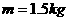的物块(可视为质点)在水平恒力F作用下，从水平面上A点由静止开始运动，运动一段距离撤去该力，物块继续滑行停在B点，已知A、B两点间的距离，物块与水平面间的动摩擦因数，求恒力F多大。()

机械能每日一题答案

(10月10日)、1、(1)从A到B的过程中，人与雪橇损失的机械能为:

ΔE=(70×10×20+×70×2.0²－×70×12.0²)J＝9100J

(2)人与雪橇在Bc段做减速运动的加速度:

根据牛顿第二定律　 :f=ma=70×(-2)N=-140N

2、如图所示，质量m_A为4.0kg的木板A放在水平面C上，木板与水平面间的动摩擦因数μ为0.24，木板右端放着质量m_B为1.0kg的小物块B(视为质点)，它们均处于静止状态。木板突然受到水平向右的12NŸs的瞬时冲量I作用开始运动，当小物块滑离木板时，木板的动能E_M为8.0J，小物块的动能为0.50J，重力加速度取10m/s²，求

⑴瞬时冲量作用结束时木板的速度v₀；

⑵木板的长度L。

(10月16日)、1、荡秋千是大家喜爱的一项体育运动。随着科技迅速发展，将来的某一天，同学们也会在其它星球上享受荡秋千的乐趣。假设你当时所在星球的质量是M、半径为R，可将人视为质点，秋千质量不计、摆长不变、摆角小球90°，万有引力常量为G。那么，

(1)该星球表面附近的重力加速度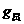等于多少？

(2)若经过最低位置的速度为v₀，你能上升的最大高度是多少？