3．类比是一种有效的学习方法，通过归类和比较，有助于掌握新知识，提高学习效率．在类比过程中，既要找出共同之处，又要抓住不同之处．某同学对机械波和电磁波进行类比，总结出下列内容，其中不正确的是(　　 )

　 　A．机械波的频率、波长和波速三者满足的关系，对电磁波也适用

　 　B．机械波和电磁波都能产生干涉和衍射现象

　 　C．机械波的传播依赖于介质，而电磁波可以在真空中传播

　　D．机械波既有横波又有纵波，而电磁波只有纵波

2．关于电磁波，下列说法正确的是　 　(　　 )

　 　A．雷达是用X光来测定物体位置的设备

　 　B．使电磁波随各种信号而改变的技术叫做解调

　 　C．用红外线照射时，大额钞票上用荧光物质印刷的文字会发出可见光

　 　D．变化的电场可以产生变化的磁场

1．下列关于电磁波的说法正确的是　　 (　　 )

　　A．电磁波必须依赖介质传播　 　B．电磁波可以发生衍射现象

　 C．电磁波不会发生偏振现象　　 D．电磁波无法携带信息传播

20.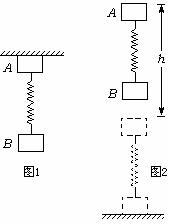如图1所示，质量分别为m和M的A、B两重物用劲度系数为k的轻质弹簧竖直地连接起来，若将A固定在天花板上，用手托住B，让弹簧处于原长，然后放手，B开始振动，试问：

(1)B到达最低点时的加速度以及弹性势能多大？

(2)B振动具有最大速度V_m时弹簧的弹性势能为多大？

(3)如图2所示，若将A从天花板上取下，使弹簧为原长时，让两物从静止开始自由下落，下落过程中弹簧始终保持竖直状态。当重物A下落距离h时，重物B刚好与地面相碰，假定碰后的瞬间重物B动能立即消失，静止于地面但不与地面粘连。为使重物A反弹时能将重物B提离地面，下落高度h至少应为多少？

解析：

(1)B释放时，弹簧原长，∴M加速度 a=g向下

当B到达最低点时，根据对称性a′=g向上

最高点与最低点回复力大小相等，即Mg=kx-Mg　

∴最低点伸长量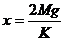

由最高点到最低点能量守恒得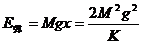

(2)B速度最大时，弹簧振子处于平衡位置，设伸长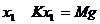

能量守恒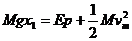　

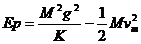
(3)B触地时，弹簧为原长，A的速度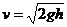，A压缩弹簧后向上弹起，弹簧恢复原长后A又继续上升拉伸弹簧，当v_A=0时，弹簧伸长x₂，B恰好被提离地面应有 Kx₂=Mg　 ∴x₂=x₁　　 ∴最高点弹性势能Ep′=Ep

弹簧由压缩到拉伸能量守恒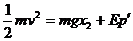

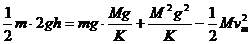
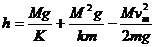
19. 某有线制导导弹发射时，在导弹发射基地和导弹间连一根细如蛛丝的特制光纤(象放风筝一样)，它双向传输信号，能达到有线制导作用。光纤由纤芯和包层组成，其剖面如图，其中纤芯材料的折射率n₁=2，包层折射率n₂=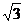，光纤长度为3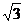km。(已知当光从折射率为n₁的介质射入折射率为n₂的介质时，入射角θ₁、折射角θ₂间满足关系：n₁sinθ₁= n₂sinθ₂)

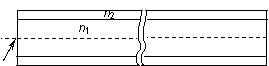⑴试通过计算说明从光纤一端入射的光信号是否会通过包层“泄漏”出去；

⑵若导弹飞行过程中，将有关参数转变为光信号，利用光纤发回发射基地经瞬间处理后转化为指令光信号返回导弹，求信号往返需要的最长时间

解：(15分)⑴由题意在纤芯和包层分界面上全反射临界角C

满足：n₁sinC = n₂sin90°(2分)得：C = 60°(1分)

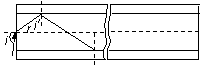当在端面上的入射角最大(i_M = 90°)时，折射角r也最大，在纤芯与包层分界面上的入射角i′最小。在端面上：i_M = 90°时，由n₁ =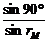(2分)　 得：r_M =30° (1分)

这时i_min′ = 90°－30°= 60°= C，所以，在所有情况中从端面入射到光纤中的信号都不会从包层中“泄漏”出去。(2分)

⑵当在端面上入射角最大时所用的时间最长，这时光在纤芯中总路程：S=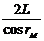(3分)

光纤中光速：v=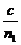(2分)，时间t =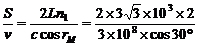s = 8×10^－5s(2分)

18.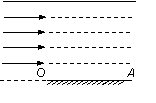 某种液体的折射率为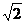,在其液面下有一可绕水平轴O匀速转动的平面镜OA，OA的初始位置与液面平行,如图18所示。在液面与平面镜间充满自左向右的平行光线。若在平面镜逆时针匀速旋转一周的过程中，光线射入空气中的时间为2s 。试问:

(1)平面镜由初始位置转过多大角度时，光线开始进入空气?

(2)平面镜旋转的角速度多大?

解：

(1)设临界角为C,则

sinC=

故　　 C=45°

由此可知当平面镜转过α₁=22.5°时光线开始进入空气.

(2)当平面镜转过67.5°时，光线又发生全反射，不能进入空气，

所以平面镜转过22.5°-67.5°间光线能进入空气

平面镜转动的角速度ω=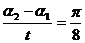rad/s

17. 图示是一透明的圆柱体的横截面，其半径R＝20cm，折射率为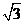，AB是一条直径，今有一束平行光沿AB方向射向圆柱体，试求：

(1)光在圆柱体中的传播速度；

(2)距离直线AB多远的入射光线，折射后恰经过B点.

解析：①光在圆柱体中的传播速度

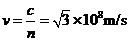
②设光线PC经折射后经过B点，光路图如图所示

由折射定律有：　　　　

又由几何关系有：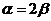 　　

解①②得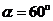　

光线PC离直线AB的距离CD=Rsinα＝10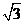cm

则距离直线AB10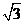cm的入射光线经折射后能到达B点．

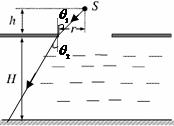
16.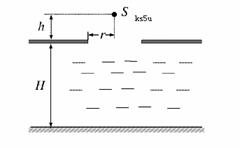在水面上放置一个足够大的遮光板，板上有一个半径为r的圆孔，圆心的正上方h 处放一个点光源S，在水面下深H处的底部形成半径为R的圆形光亮区域(图中未画出)．测得r=8cm，h=6cm，H=24cm，R=26cm，求水的折射率

解析：根据光路图，可知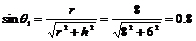

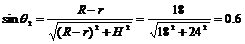
由折射定律得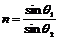，得n= 　　

15.在“用单摆测定重力加速度”的实验中：

(1)测定加速度时，测出不同的摆长L所对应的周期值T如下表所示，在题图中给出的坐标纸中作出T²-L图线，由图线可知，T²与L的关系式为，T²= 　　　　　　　。

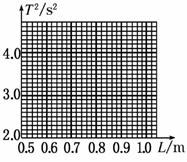
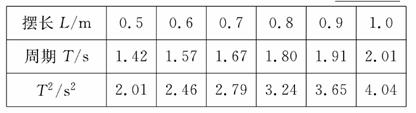
(2)利用图线上任意两点A、B的坐标(x₁,y₁)、(x₂,y₂)，可求出图线的斜率K= 　　　　　　，再由K可求出g=　　　　　　　　 　

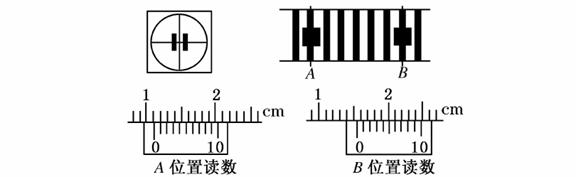
14.利用双缝干涉测定光的波长的实验中，双缝间距d=0.4mm，双缝到光屏间的距离l=0.5m，用某种单色光照射双缝得到干涉条纹如图所示，分划板在图中A、B位置时游标卡尺读数也如图中所给出，则：

(1)分划板在图中A、B位置时游标卡尺读数分别为X_A=　　　　 mm，X_B=　　　　 mm，相邻两条纹间距∆x=　　　　　 mm；

(2)波长的表达式λ=　　　　 (用∆x、l、d表示)，该单色光的波长λ=　　　　 m

(3)若改用频率较高的单色光照射，得到的干涉条纹间距将　　　　　 (填“变大”、“不变”或“变小”)。