
题目列表(包括答案和解析)
14.某同学在“用单摆测定重力加速度”的实验中,所用摆球密度不均匀,无法确定重心.他第一次测得悬线长l1(未加入摆球半径),周期为T1;第二次测得悬线长为l2,周期为T2.根据上述数据,可以确定当地的g值为多少?
答案:g=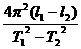
解析:设摆球重心距球心上表面距离为r,则
T1=2π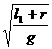 ①
①
T2=2π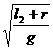 ②
②
由①②得r=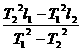 ③
③
③代入①得g=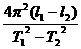 .
.
13.在用滴水法测重力加速度这个实验中,使一个水滴碰到盘子时恰好有另一水滴从水龙头开始下落.测出水龙头到盘子间距离为h m,再用秒表测时间.从第一个水滴到达盘中开始计时,到第n个水滴落至盘中,共用时间为T s,重力加速度g=______________.
答案:2(n-1)2h/T2
解析:当第一个水滴到达盘中时开始计时至第n个水滴落至盘中,所用时间为T s,则两个相邻的水滴所用时间为t=T/(n-1),而这个时间恰好是一个水滴下落h m的时间,由h=gt2/2得g=2h/t2=2(n-1)2h/T2.
12.在“用单摆测定重力加速度”的实验中,单摆的摆角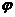 应___________.从摆球经过_________开始计时,测出n次全振动的时间为t,用毫米刻度尺测出摆线长为l,用螺旋测微器测出摆球的直径为d.
应___________.从摆球经过_________开始计时,测出n次全振动的时间为t,用毫米刻度尺测出摆线长为l,用螺旋测微器测出摆球的直径为d.
(1)用上述物理量的符号写出测定重力加速度的一般表达式为g=______________.
(2)实验中某同学发现他测出的重力加速度值总是偏大,其原因可能是______________.
A.实验室处在高山上,离海平面太高
B.单摆所用的摆球太重
C.测出n次全振动的时间为t,误作为(n+1)次全振动的时间进行计算
D.以摆球直径与摆线之和作为摆长来计算
答案:小于5° 平衡位置
(1)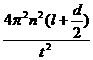
(2)CD
解析:(1)因为g=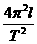 ①
①
T=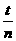 ,l′=(l+
,l′=(l+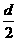 )代入①
)代入①
得:g=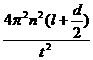 .
.
(2)C正确,由于T测<T真
所以g测>g真.
D正确:l测=(l+d)>l真
所以g测>g真.
A错:高山上比海平面g小
g测<g真.
B错:g与摆球质量无关.
11.下图为一单摆振动30次秒表的指示位置,秒表的读数是_________ s,单摆周期是_________s.

答案:35.2 1.17
10.在“用单摆测定重力加速度”的实验中:
(1)摆动时偏角应满足的条件是_______________.为了减小测量周期的误差,计时开始时,摆球应是经过最__________(填“高”或“低”)点的位置,且用秒表测量单摆完成多次全振动所用的时间,求出周期;
(2)用最小刻度为1 mm的刻度尺测摆长,测量情况如图所示,O为悬挂点.从图中可知单摆的摆长为___________m;
(3)若用l表示摆长,T表示周期,那么重力加速度的表达式为g=_____________.

答案:(1)偏角小于5° 低
(2)0.995 0
(3)4π2l/T2
9.在做“用单摆测定重力加速度”的实验时,用摆长l和周期T计算重力加速度的公式是g=__________.如果已知摆球直径为2.00 cm,用刻度尺的零刻线对准摆线的悬点,摆线竖直下垂,如图(甲)所示,那么单摆摆长是____________.如果测定了40次全振动的时间如图(乙)中秒表所示,那么秒表读数是___________ s.单摆的摆动周期是___________ s.
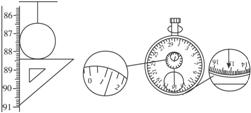
答案: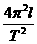 0.874 0 m或87.40 cm 75.2 1.88
0.874 0 m或87.40 cm 75.2 1.88
解析:40次通过最低点时,按下秒表停止计时,读出这段时间t,算出单摆的周期T=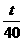 ;将所测得的l和T代入单摆的周期公式T=2π
;将所测得的l和T代入单摆的周期公式T=2π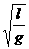 ,算出g.单摆的摆长应等于测量值88.40
cm减掉摆球的半径1 cm,得到87.40 cm.
,算出g.单摆的摆长应等于测量值88.40
cm减掉摆球的半径1 cm,得到87.40 cm.
8.在“用单摆测定重力加速度”的实验中:
(1)为了比较准确地测量出当地的重力加速度值,应选用下列所给器材中的哪些?将你所选用的器材前的字母填在题后的横线上.
A.长1 m左右的细绳; B.长30 cm左右的细绳; C.直径2 cm的铅球;
D.直径2 cm的铁球; E.秒表; F.时钟;
G.分度值是1 cm的直尺;
H.分度值是1 mm的直尺.
所选器材是____________________.
(2)实验时对摆球偏离竖直线的要求是;理由是____________________.
答案:(1)A、C、E、H (2)偏角要求小于5° 理由见解析
解析:(1)根据本实验的原理:振动的单摆,当摆角小于5°时,其振动周期与摆长的平方根成正比,与重力加速度的平方根成反比,而与偏角的大小(振幅)、摆球的质量无关,周期公式为:T=2π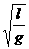 .经变换得g=
.经变换得g=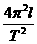 .因此,在实验中只要测出单摆的摆长l和振动周期T,就可以求出当地的重力加速度g的值,本实验的目的是测出g的值,而不是验证单摆的振动规律.如果在实验中选用较短的摆线,既会增大摆长的测量误差,又不易于保证偏角θ小于5°.摆线较长,摆角容易满足小于5°的要求,单摆的振动缓慢,方便计数和计时,所以应选A.摆球应尽量选重的,所以选C.
.因此,在实验中只要测出单摆的摆长l和振动周期T,就可以求出当地的重力加速度g的值,本实验的目的是测出g的值,而不是验证单摆的振动规律.如果在实验中选用较短的摆线,既会增大摆长的测量误差,又不易于保证偏角θ小于5°.摆线较长,摆角容易满足小于5°的要求,单摆的振动缓慢,方便计数和计时,所以应选A.摆球应尽量选重的,所以选C.
因为单摆振动周期T的测量误差对重力加速度g的影响较大,所以计时工具应选精确度高一些的秒表.摆长的测量误差同时对g的影响较大,也应选精度较高的最小刻度为毫米的直尺.
(2)因为当摆球振动时,球所受的回复力F=mgsinθ,只有当θ<5°时,sinθ≈θ,此摆才称为单摆,其振动才是简谐运动,周期T=2π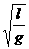 的关系式才成立.
的关系式才成立.
7.一位同学用单摆做测定重力加速度的实验,他将单摆挂起后,进行了如下步骤:
A.测摆长l:用米尺量出摆线的长度
B.测周期T:将摆球拉起,然后放开,在摆球某次通过最低点时,按下秒表开始计时,同时将此次通过最低点作为第一次,接着一直数到摆球第60次通过最低点时,按秒表停止计时,读出这段时间t,算出单摆的周期T=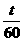
C.将所测得的l和T代入单摆的周期公式T=2π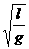 ,算出g,将它作为实验的最后结果写入报告中去
,算出g,将它作为实验的最后结果写入报告中去
指出上面步骤中遗漏或错误的地方,写出该步骤的字母,并加以改正.
_______________________________________________________________________________
_______________________________________________________________________________
答案:A.要用卡尺量出摆球直径d,摆长l等于摆线长与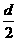 之和;B.T=
之和;B.T= ;C.g应多测几次,然后取平均值作为实验的最后结果.
;C.g应多测几次,然后取平均值作为实验的最后结果.
解析:本题偏重实验操作中的注意事项.测摆长应测出摆球的重心到悬点的距离.要用游标卡尺测摆球直径d,摆长l等于“摆的长加d/2”.
测周期是关键,也是本题难点、易错点.题中所述从第1次到第60次通过最低点,经历的时间是(60-1)/2=29.5个周期,所以T=t/29.5.
在数据处理上,应分别对l和T测量多次,求出它们的平均值l和T,然后代入公式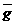 =4π2l/T2,求出的g值才可以作为实验最终结果.也可以测多次l和T,用g=4π2l/T2算出多个g值,再用g=(g1+g2+…+gn)/n求平均值.多次测量求平均值的目的是为了克服偶然误差.
=4π2l/T2,求出的g值才可以作为实验最终结果.也可以测多次l和T,用g=4π2l/T2算出多个g值,再用g=(g1+g2+…+gn)/n求平均值.多次测量求平均值的目的是为了克服偶然误差.
6.某同学在做“用单摆测定重力加速度”的实验时,如果测得的g值偏小,可能的原因是( )
A.测摆线长时摆线拉得过紧
B.摆线上端悬点未固定,振动中出现松动使摆线长度增大了
C.开始计时时,迟按秒表
D.实验中误将49次全振动计为50次全振动
答案:B
解析:因为g=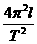 ,l测<l真
,l测<l真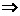 g测<g真,B正确.
g测<g真,B正确.
对于A:l测>l真,g测>g真
对于C:T测<T真,g测>g真
对于D:T测<T真,g测>g真
5.某学生利用单摆测定重力加速度,在以下各实验步骤中,有错误的步骤是( )
A.在未悬挂之前先测定好摆长
B.测得的摆长为10 cm
C.将摆球拉离平衡位置,摆角约15°后,让其在竖直平面内振动
D.测单摆周期时,应从摆球通过平衡位置开始计时
答案:ABC
解析:应在悬挂好后,利用米尺来测量摆长,A错.测出的摆长不能是10 cm,这样l不满足单摆条件l>>R,B错.将摆球拉离平衡位置,摆角应小于5°,C错,只有D正确.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com