
题目列表(包括答案和解析)
3.单摆振动中,当摆球在两边最大位移处时,则( )
A.速度最小,势能最大,绳中张力最大 B.速度最大,势能最小,绳中张力最小
C.速度最小,势能最大,绳中张力最小 D.速度最大,势能最小,绳中张力最大
答案:C
解析:单摆振动中,摆球在最大位移处时,速度最小,势能最大,绳中张力最小.当v=0时,F向=mv2/R,即F向=0,此时沿绳方向F绳-mgcosθ=0,F绳=mgcosθ,此时F绳最小.
2.下列说法中正确的是( )
A.阻尼振动一定是减幅振动
B.物体做阻尼振动时,随着振幅的减少,频率也不断减小
C.受迫振动稳定时的频率等于驱动力的频率,与物体的固有频率无关
D.受迫振动的频率由驱动力和物体结构特点共同决定
答案:C
解析:物体做阻尼振动时,如果有恰当的能量补充,也可以保持振幅不变,做等幅运动,所以阻尼振动的振幅是不一定改变的,所以A错误.
物体做阻尼振动时,振幅虽然不断减小,但是振动的频率仍由自身的结构特点所决定,不随振幅的减小而变化,所以B错误.
受迫振动稳定时的频率,只是决定于驱动力的频率,与物体自身结构特点无关,即与物体的固有频率无关,所以D错误,C正确.
1.做简谐运动的弹簧振子,其质量为m,最大速率为v,则下列说法中正确的是( )
A.振动系统的最大弹性势能为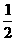 mv2
mv2
B.当振子的速率减为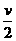 时,此振动系统的弹性势能为
时,此振动系统的弹性势能为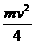
C.从某时刻起,在半个周期内,弹力做的功一定为零
D.从某时刻起,在半个周期内,弹力做的功一定为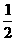 mv2
mv2
答案:AC
解析:根据简谐运动机械能守恒的特点判断A选项正确.当振子的速率减为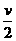 时,振子的动能减少
时,振子的动能减少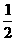 mv2-
mv2-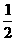 m(
m(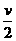 )2=
)2= mv2,那么振动系统的弹性势能为
mv2,那么振动系统的弹性势能为 mv2,B选项错误.从某时刻起经过半个周期,振子回到原位置或者回到关于平衡位置对称的位置,经过半个周期振子的速率恢复到原来的数值,所以动能不变,根据动能定理,弹力做功为零,C选项正确,D选项错误.
mv2,B选项错误.从某时刻起经过半个周期,振子回到原位置或者回到关于平衡位置对称的位置,经过半个周期振子的速率恢复到原来的数值,所以动能不变,根据动能定理,弹力做功为零,C选项正确,D选项错误.
14.如图所示为一块涂有碳黑的玻璃板,质量为2 kg,在拉力F的作用下,由静止开始竖直向上做匀变速运动,一个装有水平振针的频率为5 Hz的固定电动音叉在玻璃板上画出了图示曲线,量得OA=1 cm,OB=4 cm,OC=9 cm,试求外力的大小.(g取10 m/s2)
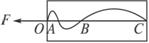
答案:F=24 N
解析:根据题意可知振针的周期为T=1/5 s=0.2 s,图中OA、AB、BC三段,均为半个周期的运动情况,所以运动时间为t=T/2=0.1 s,玻璃板的运动为匀变速运动,设其加速度为a,则由运动学公式可得:
a=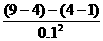 ×10-2
m/s2=2 m/s2,
×10-2
m/s2=2 m/s2,
由牛顿第二定律得:F=mg+ma=24 N.
13.甲、乙两弹簧振子质量相等,其振动图象如图所示,则它们振动的机械能大小关系是E甲___________E乙(填“>”“=”或“<”);振动频率的大小关系是f甲____________f乙;在0-4 s内,甲的加速度为正向最大的时刻是____________,乙的速度为正向最大的时刻是____________.
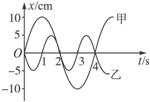
答案:> < 3 s末 1 s、3 s末两时刻
解析:想象甲、乙两弹簧振子沿x轴振动,O为其平衡位置,则联系图象可知,甲的振幅大于乙的振幅,故有E甲>E乙;甲的周期大于乙的周期,故有f甲<f乙;联系甲弹簧振子在第一周期内沿x轴的振动情形可知,在3 s时刻,甲正在负向最大位移处,弹簧伸长量最大,故此刻有最大的正向加速度.当物体通过平衡位置时速度最大.联系乙弹簧振子沿x轴振动的前两个全振动的情景,由图象知乙在1 s、3 s末两个时刻沿x轴正向通过平衡位置,故这两时刻有正向最大速度.
12.一质点做简谐运动,其位移x与时间t的关系如图所示,在t=4 s时,质点的( )
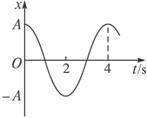
A.速度为正的最大值,加速度为零 B.速度为负的最大值,加速度为零
C.速度为零,加速度为正的最大值 D.速度为零,加速度为负的最大值
答案:D
解析:由题图可知t=4 s时,质点位于正向最大位移处,即x>0,且x=xm=A.由回复力公式F=-kx可知,回复力为负的最大值,所以加速度为负的最大值,此时质点的速度等于零,所以答案为D.
11.一人观察竖直方向上的弹簧振子,开始观察时,振子正好在平衡位置,且向下振动,经过1 s后,振子第一次回到平衡位置,且通过了10 cm的路程.选竖直向上为正方向,试画出观察到的振子的振动图象.
答案:见解析
解析:分析已知,T=2 s,A=5 cm,故振动图象为:选竖直向上方向为正
拓展应用·跳一跳,够得着!
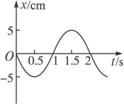
10.在上题中,8 s内甲、乙两物体通过的路程之比是____________.0-8 s时间内甲、乙动能都达到最大的时刻是____________.从2 s时刻算起,甲在____________ s时刻止完成一次全振动,乙在____________ s时刻止完成一次全振动.
答案:4∶1 4 s 6 10
解析:由图中可知:8 s内,甲物体运动两个周期,走过的路程为8×2 cm=16 cm,乙物体运动1个周期,走过的路程为4×1 cm=4 cm,所以8 s内路程之比为4∶1;动能最大时刻应该出现在平衡位置,甲、乙都达到动能最大即在4 s末;从2 s时刻算起,甲、乙在一个周期内完成一次全振动,所以为6 s和10 s时刻.
9.如图所示是甲、乙两物体分别做简谐运动的图象.由图象可知,它们的振幅A甲=________,A乙=________,频率f甲=________,f乙=________.
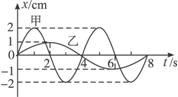
答案:2 cm 1 cm 0. 25 Hz 0.125 Hz
解析:由图中直读振幅分别为2 cm、1 cm;周期分别为4 s、8 s,所以频率分别是0.25 Hz、0.125 Hz.
8.一卡车在水平道路上行驶,货物随车厢上下振动而不脱离底板,设货物的振动为简谐运动,以向上的方向为正,其振动图象如图所示,在图象上取a、b、c、d四点,则哪点代表的时刻货物对车厢底板压力大于货物的重力( )
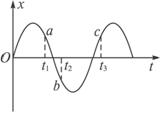
A.a点 B.b点 C.c点 D.d点
答案:BC
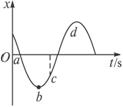
解析:如果货物对车厢底板压力大于货物的重力,则依据牛顿第三定律可知:
车厢底板对货物的支持力,在大小上大于货物的重力.
对货物受力分析可知,货物受自身重力和车底板对它的支持力.且合力方向向上.即物体处于超重状态,加速度方向向上.
在卡车运动过程中,货物在竖直方向上做上、下振动,振动图象如图所示,则加速度向上的点有:b点、c点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com