
题目列表(包括答案和解析)
45.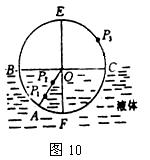 某校开展研究性学习,某研究小组根据光学知识,设计了一个测液体折射率的仪器。如图10,在一个圆盘上,过其圆心O作两条相互垂直的直径BC、EF。在半径OA上,垂直盘面插上两枚大头针P1、P2并保持位置不变。每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2。同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据P3所插的位置,就可以直接读出液体折射率的值。
某校开展研究性学习,某研究小组根据光学知识,设计了一个测液体折射率的仪器。如图10,在一个圆盘上,过其圆心O作两条相互垂直的直径BC、EF。在半径OA上,垂直盘面插上两枚大头针P1、P2并保持位置不变。每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察P1、P2。同学们通过计算,预先在圆周EC部分刻好了折射率的值,这样只要根据P3所插的位置,就可以直接读出液体折射率的值。
①若∠AOF=30°,OP3与OC之间的夹角为45°,则在P3处刻的折射率应多大?
②若在同一液体中沿AO方向射入一束白光,最靠近0C边的是哪种颜色的光?增大入射角度,哪种颜色的光在刻度盘上先消失?
解析:①P3 应刻的折射率 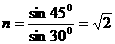
② 最靠近0C边的是紫光;
增大入射角度,紫光在刻度盘上最先消失
44. 如图所示,由红、紫两种单色光组成的光束a,以入射角i从平行玻璃板上表面O点入射.已知平行玻璃板厚度为d,红光和紫光的折射率分别为n1和n2,真空中的光速为c.试求:
如图所示,由红、紫两种单色光组成的光束a,以入射角i从平行玻璃板上表面O点入射.已知平行玻璃板厚度为d,红光和紫光的折射率分别为n1和n2,真空中的光速为c.试求:
(1)红光在玻璃中传播的速度;
(2)红光和紫光在下表面出射点 之间的距离.
之间的距离.
解析:(1)v=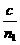 (2)如图,设红光折射角为γ1,紫光折射角为γ2,根据折射定律有: 红光 n1=
(2)如图,设红光折射角为γ1,紫光折射角为γ2,根据折射定律有: 红光 n1=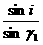
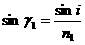
cosγ1=
tanγ1=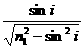
同理,紫光 n2=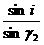 tanγ2=
tanγ2=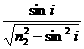
解得 Δx=d tanγ1-d tanγ2
=dsini(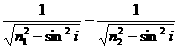 )
)
43.如图所示,某同学利用方格坐标纸测定半圆形玻璃砖的折射率,OA是画在纸上的直线,他在直线OA适当位置先后竖直插上P1、P2两枚大头针,如图放上玻璃砖(如粗黑线所示),然后插上P3、P4大头针。
①其中他确定P3大头针位置的方法应当是: 。
②若该同学实验操作规范准确,其记录的情况如图所示。该同学还用圆规做了一个以O为圆心,半径与玻璃砖相同的半圆(如图中虚线所示)。请您帮这位同学算出玻璃砖的折射率,写出必要的计算过程。
(2)本小题考查用插针法测定玻璃折射率的实验数据处理方法。
答案-①透过玻璃砖看,P3大头针挡住P1、P2两枚大头针的像。
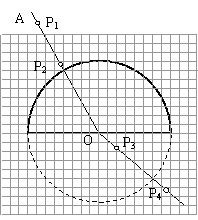 ②如图,由折射定律可得:
②如图,由折射定律可得:
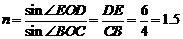
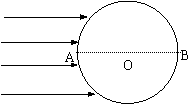
42.  如图,一透明球体置于空气中,球半径R=10cm,折射率n=
如图,一透明球体置于空气中,球半径R=10cm,折射率n=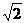 .MN是一条通过球心的直线,单色细光束AB平行于MN
.MN是一条通过球心的直线,单色细光束AB平行于MN 射向球体,B为入射点, AB与MN间距为5
射向球体,B为入射点, AB与MN间距为5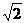 cm,CD为出射光线.
cm,CD为出射光线.
①补全光路并求出光从B点传到C点的时间;
②求CD与MN所成的角α.(需写出求解过程)
 解析:①连接BC,如图
(1分)
解析:①连接BC,如图
(1分)
在B点光线的入射角、折射角分别
标为i、r,
Sini=5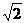 /10=
/10=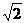 /2, 所以,
/2, 所以,
i=45°(1分)
由折射率定律:
在 B点有:
B点有: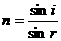 (1分)
(1分)
Sin r=1/2
故:r=30° (1分)
BC=2Rcos r (1分)
t= BCn/C=2Rncos r/C(1分)
t=(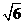 /3) ×10-9s (1分)
/3) ×10-9s (1分)
②由几何关系可知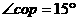 (1分)
(1分) 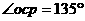 α=30°(2分)
α=30°(2分)
41.(江苏省宿迁市2008-2009学年度高三年级第一次调研测试)如图所示,一单色光束a,以入射角i=60°从平行玻璃砖上表面O点入射.已知平行玻璃砖厚度为d=10cm,玻璃对该单色光的折射率为n= .则光束从上表面进入玻璃砖的折射角为 ▲ ,光在玻璃砖中的传播的时间为 ▲ .
.则光束从上表面进入玻璃砖的折射角为 ▲ ,光在玻璃砖中的传播的时间为 ▲ .


答案-r=30° 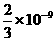 s(4分)
s(4分)
40.(1)下列说法中正确的是( )
A.把调准的摆钟,由北京移至赤道,这个钟将变慢,若 要重新调准,应增加摆长
要重新调准,应增加摆长
B.振动的频率越高,则波传播一个波长的距离所用的时间越短
C.1905年爱因斯坦提出的狭义相对论是以相对性原理和光速不变原理这两条基本假设为前提的
D.调谐是电磁波发射应该经历的过程,调制是电磁波接收应该经历的过程
E.日光灯启动时,启动器内的玻璃泡中的氖气发出红光,这是由于氖原子的外层电子受激发而产生的
F.照相机等的镜头涂有一层增透膜, 其厚度应为入射光在真空中波长的1/4 ;拍摄玻璃橱窗内的物品时,往往在镜头前加一个偏振片以增加透射光的强度
(2)如图所示,在真空中波长为600nm的激光束从A点射入圆形玻璃介质。
 ①试证明:无论入射角多大,该激光束都能从玻璃中射出。
①试证明:无论入射角多大,该激光束都能从玻璃中射出。
②若该激光束经折射从B点射出,射出玻璃与射入玻璃的光线夹角为30°,AB弧所对的圆心角为120°,求该激光束在玻璃中的波长。
解析:(1)BCE(4分,全选对的得4分,选不全的,选对一个得1分,错选或多选一个扣1分,扣完为止)
(2)①证明:设从A点入射的入射角为θ1,折射角为θ2,根据对称性,射出时的入射角也为θ2 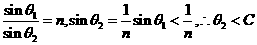 ,所以无论入射角多大,该激光束都能从玻璃中射出(4分)
,所以无论入射角多大,该激光束都能从玻璃中射出(4分)
②
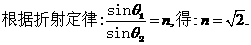 (2分)
(2分)
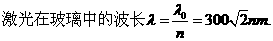 (2分)
(2分)
39.如图所示,玻璃球的半径为R,折射率n=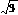 ,今有一束平行光沿直径AB方向照射在玻璃球上,试求离AB多远的入射光线最终射出后沿原方向返回。
,今有一束平行光沿直径AB方向照射在玻璃球上,试求离AB多远的入射光线最终射出后沿原方向返回。

 解析:由光路图知
解析:由光路图知
θ1=2θ2 ①
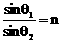 ②
②
解①②式得
cosθ2=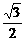 即θ2=30° θ1=60° ③
即θ2=30° θ1=60° ③
∵d=Rsinθ1 ④
∴d=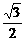 R ⑤
R ⑤
评分标准:②2分,①③④⑤各1分
38.据报道:2008年北京奥运会时,光纤通信网将覆盖所有奥运场馆,为各项比赛提供安全可靠的通信服务.光纤通信利用光的全反射将大量信息高速传输.如图所 示,一根长为L的直光导纤维,它的折射率为n.如果把该光纤放在空气中,要使从它的一个端面进入光纤的光发生全反射,最大的入射角是多少(用该角的正弦函数值表示)?为简化问题,光纤外套忽略不计.
示,一根长为L的直光导纤维,它的折射率为n.如果把该光纤放在空气中,要使从它的一个端面进入光纤的光发生全反射,最大的入射角是多少(用该角的正弦函数值表示)?为简化问题,光纤外套忽略不计.

解析: 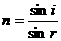 ………………2分
………………2分
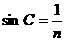 ………………2分
………………2分
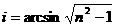 ……………2分
……………2分
37. 如图所示,一束平行单色光由空气斜射入厚度为h的玻璃砖,入射光束与玻璃砖上表面夹角为θ,入射光束左边缘与玻璃砖左端距离为b1,经折射后出射光束左边缘与玻璃砖的左端距离为b2,可以认为光在空气中的速度等于真空中的光速c.求:光在玻璃砖中的传播速度v.
如图所示,一束平行单色光由空气斜射入厚度为h的玻璃砖,入射光束与玻璃砖上表面夹角为θ,入射光束左边缘与玻璃砖左端距离为b1,经折射后出射光束左边缘与玻璃砖的左端距离为b2,可以认为光在空气中的速度等于真空中的光速c.求:光在玻璃砖中的传播速度v.
 解析:由光的折射定律得
解析:由光的折射定律得 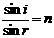 (1分)
(1分)
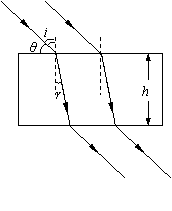 又
又
 (1分)
(1分)
由几何关系得 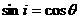 (1分)
(1分)
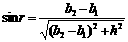 (1分)
(1分)
由以上各式可得 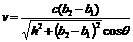 (2分)
(2分)
36.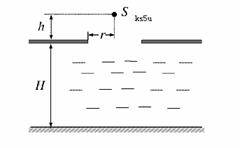 在水面上放置一个足够大的遮光板,板上有一个半径为r的圆孔,圆心的正上方h 处放一个点光源S,在水面下深H处的底部形成半径为R的圆形光亮区域(图中未画出).测得r=8cm,h=6cm,H=24cm,R=26cm,求水的折射率.
在水面上放置一个足够大的遮光板,板上有一个半径为r的圆孔,圆心的正上方h 处放一个点光源S,在水面下深H处的底部形成半径为R的圆形光亮区域(图中未画出).测得r=8cm,h=6cm,H=24cm,R=26cm,求水的折射率.
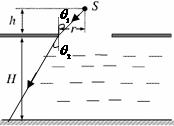 解析:根据光路图,可知
解析:根据光路图,可知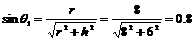 (2分)
(2分)
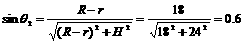 (2分)
(2分)
由折射定律得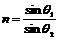 ,得n=
,得n= (2分)
(2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com