
题目列表(包括答案和解析)
2.(04上海35)在行车过程中,如果车距不够,刹车不及时,汽车将发生碰撞,车里的人可能受到伤害,为了尽可能地减轻碰撞引起的伤害,人们设计了安全带.假定乘客质量为70 kg,汽车车速为108 km/h(即30 m/s),从开始刹车到车完全停止需要的时间为5 s,安全带对乘客的作用力大小约为 ( )
A.400 N? B.600 N?? C.800 N D.1 000 N
答案 ?A
解析 根据牛顿运动定律得
F=ma=m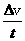 =70×
=70×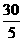 N=420 N
N=420 N
安全带对乘客的作用力大小也为420 N,和A选项相近,所以选A.
1.(06全国卷I 20)一位质量为m的运动员从下蹲状态向上起跳,经Δt时间,身体伸直并刚好离开地面,速度为v.在此过程中 ( )
A.地面对他的冲量为mv+mgΔt,地面对他做的功为 mv2?
mv2?
?B.地面对他的冲量为mv+mgΔt,地面对他做的功为零
? C.地面对他的冲量为mv,地面对他做的功为 mv2
mv2
D.地面对他的冲量为mv-mgΔt,地面对他做的功为零
答案 B?
解析 设地面对运动员的作用力为F,则由动量定理得:(F-mg)Δt=mv,故FΔt=mv+mgΔt;运动员从下蹲状态到身体刚好伸直离开地面,地面对运动员做功为零,这是因为地面对人的作用力沿力的方向没有位移.
10.(07山东理综38)在可控核反应堆中需要给快中子减速,轻水、重水和石墨等常用作减速剂.中子在重水中可与
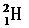 核碰撞减速,在石墨中与
核碰撞减速,在石墨中与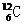 核碰撞减速.上述碰撞可简化为弹性碰撞模型.某反应堆中快中子与静止的
核碰撞减速.上述碰撞可简化为弹性碰撞模型.某反应堆中快中子与静止的
靶核发生对心正碰,通过计算说明,仅从一次碰撞考虑,用重水和石墨作减速剂,哪种减速效果更好?
答案 见解析
解析 设中子质量为mn,靶核质量为m,由动量守恒定律:
mnv0=mnv1+mv2
由能量守恒: mnv02=
mnv02= mnv12+
mnv12+ mv22
mv22
解得:v1=
在重水中靶核质量:mH=2mn,
v1H=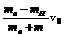 =-
=- v0
v0
在石墨中靶核质量:mC=12mn,
v1C=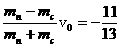 v0
v0
与重水靶核碰后中子速度较小,故重水减速效果更好.
题组二
9.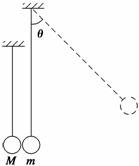 (07全国卷I24)如图所示,质量为m的由绝缘材料制成的球与质量为M=19m
(07全国卷I24)如图所示,质量为m的由绝缘材料制成的球与质量为M=19m
的金属球并排悬挂.现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,下
摆后在最低点处与金属球发生弹性碰撞.在平衡位置附近存在垂直于纸面的磁
场.已知由于磁场的阻尼作用,金属球将于再次碰撞前停在最低点处.求经过几
次碰撞后绝缘球偏离竖直方向的最大角度将小于45°.
答案 3次
解析 设在第n次碰撞前绝缘球的速度为vn-1,碰撞后绝缘球、金属球的速度分别为vn和Vn.由于碰撞过程中动量守恒、碰撞前后动能相等,设速度向左为正,则
mvn-1=MVn-mvn ①
 mvn-12=
mvn-12= MVn2+
MVn2+ mvn2 ②
mvn2 ②
由①、②两式及M=19m解得
vn=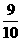 vn-1? ③
vn-1? ③
Vn=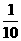 vn-1 ④
vn-1 ④
第n次碰撞后绝缘球的动能为
En= mvn2=(0.81)nE0 ⑤
mvn2=(0.81)nE0 ⑤
E0为第1次碰撞前的动能,即初始能量.
绝缘球在θ=θ0=60°与θ=45°处的势能之比为
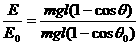 =0.586 ⑥
=0.586 ⑥
式中l为摆长.
根据⑤式,经n次碰撞后
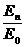 =(0.81)n ⑦
=(0.81)n ⑦
易算出(0.81)2=0.656,(0.81)3=0.531,因此,经过3次碰撞后θ将小于45°.
8.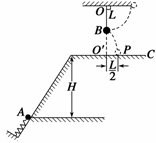 (07广东17)如图所示,在同一竖直平面上,质量为2m的小球A静止在光滑斜
(07广东17)如图所示,在同一竖直平面上,质量为2m的小球A静止在光滑斜
面的底部,斜面高度为H=2L.小球受到弹簧的弹性力作用后,沿斜面向上运动.离
开斜面后,达到最高点时与静止悬挂在此处的小球B发生弹性碰撞,碰撞后球
B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,
O点的投影O′与P的距离为L/2.已知球B质量为m,悬绳长L,视两球为
质点,重力加速度为g,不计空气阻力.求:
(1)球B在两球碰撞后一瞬间的速度大小.
(2)球A在两球碰撞前一瞬间的速度大小.
(3)弹簧的弹力对球A所做的功.
答案 (1) 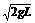 (2)
(2)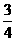
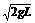 (3)
(3)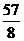 mgL
mgL
解析 (1)设碰撞后的一瞬间,球B的速度为vB′,由于球B恰能摆到与悬点O同一高度,根据动能定理
-mgL=0- mvB′2 ①
mvB′2 ①
vB′=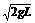 ②
②
(2)球A达到最高点时,只有水平方向速度,与球B发生弹性碰撞,设碰撞前的一瞬间,球A水平速度为vA,碰撞后的一瞬间,球A速度为vA′.球A、B系统碰撞过程由动量守恒和机械能守恒得
2mvA=2mvA′+mvB′ ③
 ×2mvA2=
×2mvA2= ×2mvA′2+
×2mvA′2+ ×mvB′2 ④
×mvB′2 ④
由②③④解得vA′=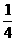
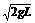 ⑤
⑤
及球A在碰撞前的一瞬间的速度大小
vA=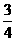
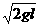 ⑥
⑥
(3)碰后球A做平抛运动.设从抛出到落地时间为t,平抛高度为y,则
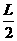 =vA′t ⑦
=vA′t ⑦
y= gt2 ⑧
gt2 ⑧
由⑤⑦⑧解得y=L
以球A为研究对象,弹簧的弹性力所做的功为W,从静止位置运动到最高点
W-2mg(y+2L)= ×2mvA2 ⑨
×2mvA2 ⑨
由⑥⑦⑧⑨得W=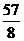 mgL
mgL
7.(07重庆理综25)某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如
右图所示.用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平
杆,球间有微小间隔,从左到右,球的编号依次为1、2、3…….N,球的质量依次递减,
每个球的质量与其相邻左球质量之比为k(k<1).将1号球向左拉起,然后由静止释放,使
其与2号球碰撞,2号球再与3号球碰撞……所有碰撞皆为无机械能损失的正碰.(不计空气阻力,忽略绳的伸长,g取10 m/s2)
(1)设与n+1号球碰撞前,n号球的速度为vn,求n+1号球碰撞后的速度.
(2)若N=5,在1号球向左拉高h的情况下,要使5号球碰撞后升高16h(16h小于绳长),问k值为多少?
(3)在第(2)问的条件下,悬挂哪个球的绳最容易断,为什么?
答案 (1) (2)0.414 (3)悬挂1号球的绳最容易断,原因见解
(2)0.414 (3)悬挂1号球的绳最容易断,原因见解
解析 (1)设n号球质量为mn,n+1号球质量为mn+1,碰撞后的速度分别为v n′、vn+1′,取水平向右为正方向,据题意有n号球与n+1号球碰撞前的速度分别为vn、0,且mn+1=kmn
根据动量守恒定律,有mnvn=mnvn′n+kmnv n+1′ ①
根据机械能守恒定律,有
 mnvn2=
mnvn2= mnv n′2+
mnv n′2+ kmnv n+1′2 ②
kmnv n+1′2 ②
由①②得v n+1′=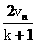 (v n+1′=0舍去)
(v n+1′=0舍去)
设n+1号球与n+2号球碰前的速度为vn+1?
据题意有vn+1=v n+1′
得vn+1=v n+1′= ③
③
(2)设1号球摆至最低点时的速度为v1,由机械能守恒定律有
m1gh= m1v12 ④
m1v12 ④
解得v1=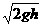 ⑤
⑤
同理可求5号球碰后瞬间的速度
v5=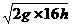 ⑥
⑥
由③式得vn+1=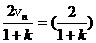 nv1 ⑦
nv1 ⑦
N=n+1=5时,v5=(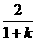 )4v1 ⑧
)4v1 ⑧
由⑤⑥⑧三式得
k=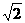 -1≈0.414(k=-
-1≈0.414(k=-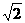 -1舍去) ⑨
-1舍去) ⑨
(3)设绳长为l,每个球在最低点时,细绳对球的拉力为F,由牛顿第二定律有
F-mng=mn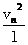 ⑩
⑩
则F=mng+mn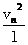 =mng+2
=mng+2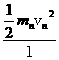 =mng+
=mng+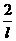 Ekn
Ekn 
? 式中Ekn为n号球在最低点的动能
式中Ekn为n号球在最低点的动能
由题意可知1号球的重力最大,又由机械能守恒定律可知1号球在最低点碰前的动能也最大,根据 式可判断在1号球碰撞前瞬间悬挂1号球细绳的张力最大,故悬挂1号球的绳最容易断.
式可判断在1号球碰撞前瞬间悬挂1号球细绳的张力最大,故悬挂1号球的绳最容易断.
6.(07四川理综25)目前,滑板运动受到青少年的追捧.如
图是某滑板运动员在一次表演时的一部分赛道在竖直平面
内的示意图,赛道光滑,FGI为圆弧赛道,半径R=6.5 m,G为最低点并与水平赛道BC位于同一水平面,KA、DE平台的高度都为h=1.8 m,B、C、F处平滑连接.滑板a和b的质量均为m,m=5 kg,运动员质量为M,M=45 kg.表演开始,运动员站在滑板b上,先让滑板a从A点静止下滑,t1=0.1 s后再与b板一起从A点静止下滑.滑上BC赛道后,运动员从b板跳到同方向运动的a板上,在空中运动的时间t2=0.6 s(水平方向是匀速运动).运动员与a板一起沿CD赛道上滑后冲出赛道,落在EF赛道的P点,沿赛道滑行,经过G点时,运动员受到的支持力N=742.5 N.(滑板和运动员的所有运动都在同一竖直平面内,计算时滑板和运动员都看作质点,取g=10 m/s2)
(1)滑到G点时,运动员的速度是多大?
(2)运动员跳上滑板a后,在BC赛道上与滑板a共同运动的速度是多大?
(3)从表演开始到运动员滑至I的过程中,系统的机械能改变了多少?
答案 (1)6.5 m/s (2)6.9 m/s (3)88.75 J?
解析 (1)在G点,运动员和滑板一起做圆周运动,设向心加速度为an,速度为vG,运动员受到重力 Mg、滑板对运动员的支持力N的作用,则
N-Mg=Man ①
an=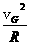 ②
②
即N-Mg=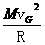 ③
③
vG=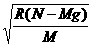 ④
④
vG=6.5 m/s ⑤
(2)设滑板a由A点静止下滑到BC赛道后速度为v1,由机械能守恒定律有
mgh= mv12 ⑥
mv12 ⑥
解得v1=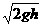 ⑦
⑦
运动员与滑板b一起由A点静止下滑到BC赛道后,速度也为v1.
运动员由滑板b跳到滑板a,设蹬离滑板b时的水平速度为v2,在空中飞行的水平位移为s,则
s=v2t2 ⑧
设起跳时滑板a与滑板b的水平距离为s0,则
s0=v1t1 ⑨
设滑板a在t2时间内的位移为s1,则
s1=v1t2 ⑩
s=s0+s1 
即v2t2=v1(t1+t2) 
运动员落到滑板a后,与滑板a共同运动的速度为v,由动量守恒定律
mv1+Mv2=(m+M)v 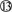
由以上方程可解出
v=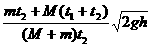
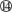
代入数据,解得v=6.9 m/s? 
(3)设运动员离开滑板b后,滑板b的速度为v3,有
Mv2+mv3=(M+m)v1
可算出v3=-3 m/s,有|v3|=3 m/s<v1=6 m/s,b板将在两个平台之间来回运动,机械能不变.
系统的机械能改变为
?ΔE= (M+m)vG2+
(M+m)vG2+ mv32-(m+m+M)gh
mv32-(m+m+M)gh
 故ΔE=88.75 J
故ΔE=88.75 J
5.(07四川理综18)如图所示,弹簧的一端固定在竖直墙上,质量为m的光滑
弧形槽静止在光滑水平面上,底部与水平面平滑连接,一个质量也为m的小球
从槽高h处开始自由下滑 ( )
A.在以后的运动过程中,小球和槽的动量始终守恒
B.在下滑过程中小球和槽之间的相互作用力始终不做功
C.被弹簧反弹后,小球和槽都做速率不变的直线运动
D.被弹簧反弹后,小球和槽的机械能守恒,小球能回到槽高h处
答案 C?
解析 小球与槽组成的系统在水平方向动量守恒,由于小球与槽质量相等,分离后小球和槽的速度大小相等,小球与弹簧接触后,由能量守恒可知,它将以原速率被反向弹回,故C项正确.
4.(07重庆理综17)为估算池中睡莲叶面承受雨滴撞击产生的平均压强,小明在雨天将一圆柱形水杯置于露台,测得1小时内杯中水位上升了45 mm.查询得知,当时雨滴竖直下落速度约为12 m/s.据此估算该压强约为(设雨滴撞击睡莲后无反弹,不计雨滴重力,雨水的密度为1×103 kg/m3?)
A.0.15 Pa B.0.54 Pa C.1.5 Pa D.5.4 Pa?
答案 A
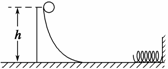 解析 设圆柱形水杯的横截面积为S,则水杯中水的质量为m=ρV=103×45×10-3S=45S,由动量定理可得:Ft=mv,而p=
解析 设圆柱形水杯的横截面积为S,则水杯中水的质量为m=ρV=103×45×10-3S=45S,由动量定理可得:Ft=mv,而p= ,所以p=
,所以p=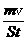 =
=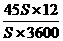 Pa=0.15 Pa.
Pa=0.15 Pa.
3.(07北京理综20)在真空中的光滑水平绝缘面上有一带电小滑块.开始时滑块静止.若在滑块所在空间加一水平匀强电场E1,持续一段时间后立刻换成与E1相反方向的匀强电场E2.当电场E2与电场E1持续时间相同时,滑块恰好回到初始位置,且具有动能Ek.在上述过程中,E1对滑块的电场力做功为W1,冲量大小为I1;E2对滑块的电场力做功为W2,冲量大小为I2.则 ( ) ?A.I1=I2 B.4I1=I 2 C.W1=0.25Ek,W2=0.75Ek? D.W1=0.20Ek,W2=0.80Ek
答案 C
解析 电场为E1时滑块的加速度为a1,电场为E2时滑块的加速度为a2,两段相同时间t内滑块运动的位移大小相等,方向相反,第一个t内的位移s1= a1t2,第二个t内的位移s2=v1t-
a1t2,第二个t内的位移s2=v1t- a2t2=a1t·t-
a2t2=a1t·t- a2t2=a1t2-
a2t2=a1t2- a2t2,由s1=-s2得:a2=3a1,即:E2=3E1,所以I1=E1qt,I2=E2qt,则I2=3I1,故A、B错误.W1=E1qs,W2=E2qs,而W1+W2=Ek,所以
a2t2,由s1=-s2得:a2=3a1,即:E2=3E1,所以I1=E1qt,I2=E2qt,则I2=3I1,故A、B错误.W1=E1qs,W2=E2qs,而W1+W2=Ek,所以
W1=0.25Ek,W2=0.75Ek,故C对,D错.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com