
题目列表(包括答案和解析)
24.(16分)如图所示,某人乘雪橇从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为60kg.表中记录了沿坡滑下过程中的有关数据,请根据图表中的数据解决下列问题:
(1)人与雪橇从A到B的过程中,损失的机械能为多少?
(2)设人与雪橇在BC段所受阻力恒定,求阻力大小(g =10m/s2)
|
位置 |
A |
B |
C |
|
速度(m/s) |
2.0 |
12.0 |
0 |
|
时刻(s) |
0 |
4 |
10 |

(1)从A到B的过程中,人与雪橇损失的机械能为: 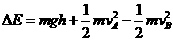
ΔE=(70×10×20+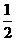 ×70×2.02-
×70×2.02-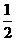 ×70×12.02)J=9100J
×70×12.02)J=9100J
(2)人与雪橇在Bc段做减速运动的加速度: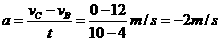
根据牛顿第二定律 :f=ma=70×(-2)N=-140N
(也可用动量定理)
23.(12分)如图所示是放置在竖直平面内的游戏滑轨,有一质量m=2kg的小球穿在轨道上滑轨由四部分粗细均匀的滑杆组成:水平直轨道AB;倾斜直轨道CD,长L=6m,与水平面间的夹角θ=370;半径R1=1m的圆弧轨道APC;半径R2=3m的圆弧轨道BQED直轨道与圆弧轨道相切,切点分别为A、B、D、C,E为最低点倾斜直轨道CD与小球间的动摩擦因数为μ=2/3,其余部分均为光滑轨道,取g=10m/s2 ,sin370=0.6,cos370=0.8现让小球从AB的正中央以初速度V0=10m/s开始向左运动,问:
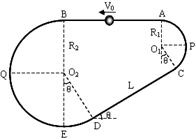 (1)第一次经过E处时,轨道对小球的作用力为多大?
(1)第一次经过E处时,轨道对小球的作用力为多大?
(2)小球第一次回到出发点时的速度为多大?
(3)小球在运动过程中,损失的机械能最多为多少?

力计算题专题训练(动力学)九
22.(10分)为了缩短下楼的时间,消防队员往往抱着竖直杆直接滑下,先以可能的最大加速度沿杆做匀加速直线运动(即自由落体运动),再以可能的最大加速度沿杆做匀减速直线运动。假设一名质量m=65kg、训练有素的消防队员(可视为质点),在沿竖直杆无初速滑至地面的过程中,重心共下移了h=11.4m,已知该队员与杆之间的滑动摩擦力最大可达到Fmax=975N,队员着地的速度不能超过6m/s,重力加速度g取10m/s2,竖直杆表面各处的粗糙程度相同,且忽略空气对该队员的作用力,求:
(1)该队员下滑过程中速度的最大值;
(2)该队员下滑过程的最短时间
解:



21.(14分)物理学中库仑定律和万有引力定律有相似的表达形式,对带异种电荷的两粒子组成的系统而言,若定义相距无穷远处电势能为零,则相距为r时系统的电势能可以表示为
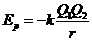 。
。
(1)若地球质量为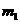 ,某人造地球卫星质量为
,某人造地球卫星质量为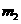 ,也定义相距无穷远处引力势能为零,写出当地心与卫星相距R时该系统引力势能表达式。(地球可看作均匀球体,卫星可看成质点)
,也定义相距无穷远处引力势能为零,写出当地心与卫星相距R时该系统引力势能表达式。(地球可看作均匀球体,卫星可看成质点)
(2)今有一颗卫星贴着地球表面绕行时速度大小为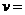 7.90km/s,当该卫星在离地面高度为
7.90km/s,当该卫星在离地面高度为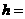
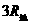 处绕行时,绕行速度
处绕行时,绕行速度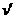 为多大?(R地为地球半径)
为多大?(R地为地球半径)
(3)若在离地面高度为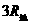 处绕行的卫星质量为1t,则至少需要对该卫星补充多大的能量才能使其脱离地球的束缚?
处绕行的卫星质量为1t,则至少需要对该卫星补充多大的能量才能使其脱离地球的束缚?
解析(1)由类比可知,该系统引力势能表达式为: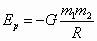
(2)由万有引力提供向心力 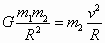
得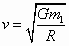 ,
, 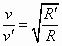
上式中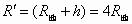
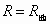
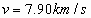
解得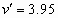 km/s
km/s
(3)卫星在该处的动能:
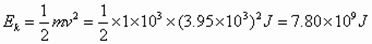
由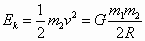
系统的势能: 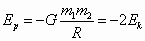
得系统的机械能: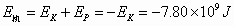
则需要给卫星补充的能量: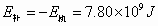
力计算题专题训练(动力学)八
20. (12分)过山车质量均匀分布,从高为h的平台上无动力冲下倾斜轨道并进入水平轨道,然后进入竖直圆形轨道,如图所示,已知过山车的质量为M,长为L,每节车厢长为a,竖直圆形轨道半径为R, L> 2πR,且R>>a,可以认为在圆形轨道最高点的车厢受到前后车厢的拉力沿水平方向,为了不出现脱轨的危险,h至少为多少?(用R.L表示,认为运动时各节车厢速度大小相等,且忽略一切摩擦力及空气阻力)
(12分)过山车质量均匀分布,从高为h的平台上无动力冲下倾斜轨道并进入水平轨道,然后进入竖直圆形轨道,如图所示,已知过山车的质量为M,长为L,每节车厢长为a,竖直圆形轨道半径为R, L> 2πR,且R>>a,可以认为在圆形轨道最高点的车厢受到前后车厢的拉力沿水平方向,为了不出现脱轨的危险,h至少为多少?(用R.L表示,认为运动时各节车厢速度大小相等,且忽略一切摩擦力及空气阻力)
取过山车为研究对象,过山车从平台上滑下到车厢占满竖直圆形轨道过程中,由于只有重力做功,故机械能守恒,竖直圆形轨道上的过山车可以把这部分的重心看作在轨道的圆心上,所以有:
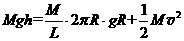 ①
①
在竖直方向受到重力和轨道对它向下的压力,受力分析如图所示,设一节车厢质量为m,则有:
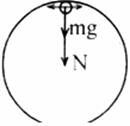
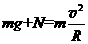 ②
②
N≥0 ③
联立解得 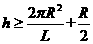
19.(12分)如图所示,M是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴 匀速转动,以经过O水平向右的方向作为x轴的正方向.在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,在t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为v.已知容器在t=0时滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水.问:
匀速转动,以经过O水平向右的方向作为x轴的正方向.在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,在t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为v.已知容器在t=0时滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水.问:
(1)每一滴水经多长时间滴落到盘面上?
(2)要使每一滴水在盘面上的落点都位于一条直线上,圆盘转动的最小角速度ω.
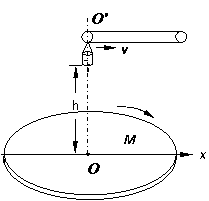 (3)第二滴水与第三滴水在盘面上的落点间的最大距离s.
(3)第二滴水与第三滴水在盘面上的落点间的最大距离s.
(1)水滴在坚直方向作自由落体运动,有
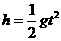 得
得 
(2)要使每一滴水在圆盘面上的落点都位于同一条直线上,在相邻两滴水的下落时间内,圆盘转过的最小角度为π,所以最小角速度为
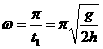
(3)第二滴水落在圆盘上的水平位移为
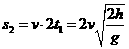
第二滴水落在圆盘上的水平位移为
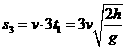
当第二滴水与第三滴水在盘面上的落点位于同一直径上圆心的两侧时两点间的距离最大,为
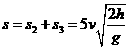
18.(12分)如图ABC是光滑半圆形轨道,轨道直径AOC沿竖直方向,长为0.8m,今有一质量为m的小球自A点以初速度v水平射入轨道内,求:
⑴小球能沿轨道运动时,水平初速度v的最小值;
⑵若小球的水平初速度小于⑴中最小值,小球有无可能经过B点?若能,求出初速度满足的条件;若不能,说明理由.(g=10m/s2)

(1)2m/s
(2)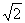 m/s
m/s
17.(12分)在一次“模拟微重力环境”的实验中,实验人员乘座实验飞艇到达6000m的高空,然后让其由静止下落,下落过程中飞艇所受空气阻力为其重力的0.04倍,实验人员可以在飞艇内进行微重力影响的实验,当飞船下落到距地面的高度为3000m时,开始做匀减速运动,以保证飞艇离地面的高度不得低于500m,重力加速度g恒取10m/s2. 试计算:
(1)飞艇加速下落的时间
(2)飞艇匀减速运动时的加速度不得小于多少?
解析: (1)设飞艇加速下落的加速度为a1 ,
由牛顿第二定律得:mg-f=ma1
解得a1=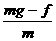 =9.6m/s2
=9.6m/s2
加速下落的高度为h1=6000-3000=3000m, h1 = 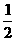 a1t 2
a1t 2
加速下落的时间为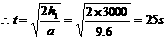
(2)飞艇开始做减速运动时的速度为 v= a1t=240m/s
匀减速下落的最大高度为 h2 =3000-500=2500m
要使飞艇在下降到离地面500m时速度为零,飞艇减速时的加速度a2至少应为
a2= 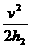 =11.5m/s2
=11.5m/s2
16、(12分)如图 12 所示,一块质量为M,长为L的均质长木板放在很长的光滑水平桌面上,板的左端有一质量为m的小物体(可视为质点),物体上连接一根很长的细绳,细绳跨过位于桌边的定滑轮.某人以恒定的速率v向下拉绳,物体最多只能到达板的中点,已知整个过程板的右端都不会到达桌边定滑轮处.试求:
(1)当物体刚达木板中点时木板的位移;
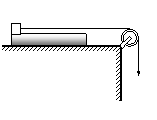 (2)若木板与桌面之间有摩擦,为使物体能达到板的右端,板与桌面之间的动摩擦因数应满足什么条件?
(2)若木板与桌面之间有摩擦,为使物体能达到板的右端,板与桌面之间的动摩擦因数应满足什么条件?
解:(1)m与M相对滑动过程
m匀速运动有 : vt = S1 (1)
M匀加速运动有:vt/2 =S2 (2)
S1 - S2 =L/2 (3)
联立以上三式得S2 = L/2
(2)设m与M之间摩擦因数为μ1
当桌面光滑时有 mgμ1 = Ma1 (4)
v2 = 2a1S2 (5)
由(4)(5)得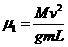
如果板与桌面有摩擦,因为M与桌面摩擦因数越大,m越易从右端滑下,所以当m滑到M右端两者刚好共速时摩擦因数最小,设为μ2
对M有: (6)
(6)
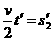 (7)
(7)
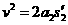 (8)
(8)
对m有:
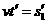 (9)
(9)
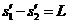 (10)
(10)
联立以上五式得 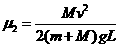
所以桌面与板间的摩擦因数μ ≥ Mv2/2(m + M)gL 。
力计算题专题训练(动力学)七
15、(12分)A、B两个小球由柔软的细线相连,线长L = 6m ,现将A 、B球先后以相同的初速度vo = 4.5m/s,从同一点水平抛出(先A 、后B)相隔时间t0= 0.8s(取g = 10m/s2)。
(1)B球抛出后经多少时间,细线刚好被拉直?(在线拉直前,两球都未落地)
(2)细线刚被拉直时,A 、B球的水平位移(相对于抛出点)各多大?
解:(1)A 球先抛出 0.8 s的时间内
水平位移so = voto = 4.5×0.8 = 3.6 m 。
竖直位移ho =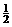 gt02 =
gt02 =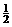 ×10×0.82 = 3.2 m 。
×10×0.82 = 3.2 m 。
A 、B球都抛出后,若 B 球以 A 球为参照物,则水平方向上的相对
速度 vBAx = 0 ,竖直方向上的相对速度 vBAy = gto = 10×0.8 = 8m/s 。
设 B 球抛出后经时间 t线被拉直,则有:
( ho + vBAy t)2 + so2 = L2
解得 t = 0.2 s ,
(2)t总 = to + t = 1 s 。
sA = vo t总= 4.5 m 。
sB = vo t = 0.9 m 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com