
题目列表(包括答案和解析)
1.弹簧振子
⑴周期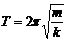 ,与振幅无关,只由振子质量和弹簧的劲度决定。
,与振幅无关,只由振子质量和弹簧的劲度决定。
⑵可以证明,竖直放置的弹簧振子的振动也是简谐运动,周期公式也是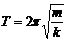 。这个结论可以直接使用。
。这个结论可以直接使用。
⑶在水平方向上振动的弹簧振子的回复力是弹簧的弹力;在竖直方向上振动的弹簧振子的回复力是弹簧弹力和重力的合力。
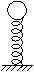 例1. 如图所示,质量为m的小球放在劲度为k的轻弹簧上,使小球上下振动而又始终未脱离弹簧。⑴最大振幅A是多大?⑵在这个振幅下弹簧对小球的最大弹力Fm是多大?
例1. 如图所示,质量为m的小球放在劲度为k的轻弹簧上,使小球上下振动而又始终未脱离弹簧。⑴最大振幅A是多大?⑵在这个振幅下弹簧对小球的最大弹力Fm是多大?
解:该振动的回复力是弹簧弹力和重力的合力。在平衡位置弹力和重力等大反向,合力为零;在平衡位置以下,弹力大于重力,F- mg=ma,越往下弹力越大;在平衡位置以上,弹力小于重力,mg-F=ma,越往上弹力越小。平衡位置和振动的振幅大小无关。因此振幅越大,在最高点处小球所受的弹力越小。极端情况是在最高点处小球刚好未离开弹簧,弹力为零,合力就是重力。这时弹簧恰好为原长。
⑴最大振幅应满足kA=mg, A=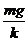
⑵小球在最高点和最低点所受回复力大小相同,所以有:Fm-mg=mg,Fm=2mg
3.从总体上描述简谐运动的物理量
振动的最大特点是往复性或者说是周期性。因此振动物体在空间的运动有一定的范围,用振幅A来描述;在时间上则用周期T来描述完成一次全振动所须的时间。
⑴振幅A是描述振动强弱的物理量。(一定要将振幅跟位移相区别,在简谐运动的振动过程中,振幅是不变的而位移是时刻在改变的)
⑵周期T是描述振动快慢的物理量。(频率f=1/T 也是描述振动快慢的物理量)周期由振动系统本身的因素决定,叫固有周期。任何简谐振动都有共同的周期公式: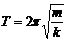 (其中m是振动物体的质量,k是回复力系数,即简谐运动的判定式F= -kx中的比例系数,对于弹簧振子k就是弹簧的劲度,对其它简谐运动它就不再是弹簧的劲度了)。
(其中m是振动物体的质量,k是回复力系数,即简谐运动的判定式F= -kx中的比例系数,对于弹簧振子k就是弹簧的劲度,对其它简谐运动它就不再是弹簧的劲度了)。
2.几个重要的物理量间的关系
要熟练掌握做简谐运动的物体在某一时刻(或某一位置)的位移x、回复力F、加速度a、速度v这四个矢量的相互关系。
⑴由定义知:F∝x,方向相反。
⑵由牛顿第二定律知:F∝a,方向相同。
⑶由以上两条可知:a∝x,方向相反。
⑷v和x、F、a之间的关系最复杂:当v、a同向(即 v、 F同向,也就是v、x反向)时v一定增大;当v、a反向(即 v、 F反向,也就是v、x同向)时,v一定减小。
1.定义
物体在跟偏离平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动,叫简谐运动。表达式为:F= -kx
⑴简谐运动的位移必须是指偏离平衡位置的位移。也就是说,在研究简谐运动时所说的位移的起点都必须在平衡位置处。
⑵回复力是一种效果力。是振动物体在沿振动方向上所受的合力。
⑶“平衡位置”不等于“平衡状态”。平衡位置是指回复力为零的位置,物体在该位置所受的合外力不一定为零。(如单摆摆到最低点时,沿振动方向的合力为零,但在指向悬点方向上的合力却不等于零,所以并不处于平衡状态)
⑷F=-kx是判断一个振动是不是简谐运动的充分必要条件。凡是简谐运动沿振动方向的合力必须满足该条件;反之,只要沿振动方向的合力满足该条件,那么该振动一定是简谐运动。
3.利用图象解题:
|
|
振动图象 |
波动图象 |
|
研究对象 |
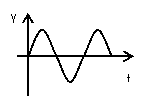 一个质点 一个质点 |
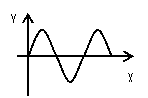 多个质点 多个质点 |
|
坐标 |
|
|
|
物理意义 |
一个质点的位移随时间变化的情况 |
同一时刻各质点离开平衡位置的情况 |
|
直接物理量 |
A 、 T |
A λ |
|
图象变化 |
随时间延续 |
随时间波形平移 |
①用振动求波动:
例1:一列简谐波沿直线传播,位于此直线上相距为2米的A、B两点的振动图象如图所示。以知这列波的波长大于1米,则此波的波长为 米;波速为 米/秒。

②波的多值问题:
例2:一根张紧的水平弹性绳上的a 、b 两点相距14米,b点在a点右方。当一列简谐波沿此绳向右传播时,若a点的位移达到正的极大时,b点的位移恰为零,且向下运动。经过1.00秒, a 点的位移为零,且向下运动,而b点位移恰达到负的极大,则这列简谐波的波速
可能是:A、4.67m/s ; B、6m/s C、10m/s D、14m/s
附:
2. 摆钟校准:
例:有一挂钟,其摆锤的振动可看成单摆,在正常运动时,摆动周期为2秒。现因调整不当,使该钟每天快3分钟,试求摆长比正常摆长缩短了多少?
解: 摆锤摆动越快,表的指针走的越快,所以表的指针转动的快
慢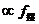 :
: 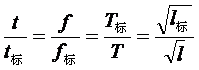 或 =
或 =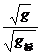
1. 等效单摆:
例1:在一升降机中悬有一单摆,以加速度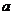 向上做匀加速度运动,则此单摆的摆动周期为多少?
向上做匀加速度运动,则此单摆的摆动周期为多少?
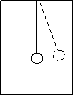
例2:已知小车中有一单摆,求小车匀速或以加速度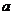 向右运动时,单摆的摆动周期?
向右运动时,单摆的摆动周期?
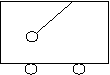
 例3:求单摆的振动周期:
例3:求单摆的振动周期:

7.特性: 干涉: 条件: 相干波源(频率相同;相差恒定)
衍射: 条件: 障碍物或孔的尺寸比波长小或相差不多
6.波的图象:同一时刻各质点离开平衡位置的情况
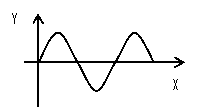
传播方向的判定: ①波峰波谷的移动方向是波的传播方向;
②小树迎风倒;
5.物理量: λ、ν、Τ(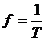 )
) 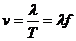
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com