
题目列表(包括答案和解析)
24.(20分)
解:(1) (5分) 设绝缘棒与金属棒碰前的速率为v1,绝缘棒在导轨由最低点向上滑动的过程中,由动能定理

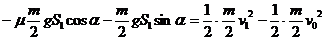 …………………… (3分)
…………………… (3分)
v1=5m/s …………………………………………………………… (2分)
(2)(10分)设碰后安培力对金属棒做功为W安,由功能关系,安培力做的功等于回路中产生的总电热
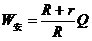 ………………………………………………………… (2分)
………………………………………………………… (2分)
W安= 0.25J …………………………………………………………… (1分)
设碰后金属棒速率为v、切割磁感线产生的感应电动势为E,回路中感应电流为I,安培力为F安
E=Bdv …………………………………………………………… (1分)
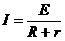 ………………………………………………………… (1分)
………………………………………………………… (1分)
F安=BId …………………………………………………………… (1分)
由动能定理
-W安-mgS2sinα-μmgS2cosα=0-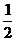 mv22 ………………………… (1分)
mv22 ………………………… (1分)
v=3m/s …………………………………………………………… (1分)
设两棒碰后瞬时金属棒的加速度为a,由牛顿第二定律
μmgcosα+mgsinα+F安= ma ……………………………………… (1分)
a = 25m/s2 ………………………………………………………… (1分)
(3)(5分)设金属棒在导轨上运动时间为t,在此运动过程中,安培力的冲量为I安,沿导轨方向,由动能定理
-I安-μmgtcosα-mgtsinα=0-mv …………………………………… (1分)
I安=Bd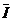 △t ……………………………………………………… (1分)
△t ……………………………………………………… (1分)
由闭合电路欧姆定律  ………………………………… (1分)
………………………………… (1分)
由法拉第电磁感应定律 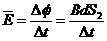 …………………………… (1分)
…………………………… (1分)
得 t = 0.2s …………………………… (1分)
丰台
23.(18分)
解:(1)(5分)设两个正点电荷在电场中C点的场强分别为E1和E2,在C点的合场强为Ec
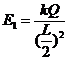 …………………………………………………………… (1分)
…………………………………………………………… (1分)
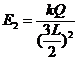 …………………………………………………………… (1分)
…………………………………………………………… (1分)
Ec=E1+E2 …………………………………………………………… (1分)
 …………………………………………………………… (2分)
…………………………………………………………… (2分)
(2)(5分)带电物块从C点运动到D点的过程中,先加速后减速。AB连线上对称点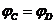 ,电场力对带电物块做功为零,设物块受到的阻力为f,由动能定理
,电场力对带电物块做功为零,设物块受到的阻力为f,由动能定理
-fL= 0-m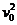 …………………………………………………………… (3分)
…………………………………………………………… (3分)
f = m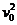 …………………………………………………………… (2分)
…………………………………………………………… (2分)
(3)(8分)设带电物块从C到O点电场力做功为W电,由动能定理
W电-
 =
n m
=
n m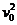 -m
-m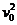 ………………………………………… (2分)
………………………………………… (2分)
W电= ………………………………………………………… (2分)
………………………………………………………… (2分)
设带电物块在电场中运动的总路程为S,由动能定理
WF-fS=0-m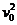 ………………………………………………………… (2分)
………………………………………………………… (2分)
S= (n+0.5)L ………………………………………………………… (2分)
22.(16分)
解:(1)(4分)物块在水平桌面上做匀加速直线运动,设加速度为a1,由牛顿第二定律
F-μmg=ma1 ……………… (2分)
a1=2 .0m/s2 ……………… (2分)
(2) (8分)设物块运动2s的位移S1、2s末的速度v1
S1 =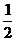 a1t12 = 4.0m
……………… (2分)
a1t12 = 4.0m
……………… (2分)
v1 = a1t1 = 4.0 m/s ……………… (2分)
撤去水平拉力后物块加速度为a2,物块离开桌面时速度为v2
a2=μg=3 m/s2 ………………………………………………………… (2分)
v22= v12-2 a2 S2 ………………………………………………………… (1分)
v2=2 .0m/s ………………………………………………………… (1分)
(3)(4分)物块离开桌面后做平抛运动,设落地点物块距桌面边缘距离为L
H= gt22 ……………………………………………………………… (1分)
gt22 ……………………………………………………………… (1分)
t2=0.5s ……………………………………………………………… (1分)
L= v2t2 ……………………………………………………………… (1分)
L=1.0m ……………………………………………………………… (1分)
24.(20分)
如图所示,两根平行金属导轨MN、PQ相距为d=1.0m,导轨平面与水平面夹角为α=30°,
导轨上端跨接一定值电阻R=1.6Ω,导轨电阻不计,整个装置处于与导轨平面垂直且向上的
匀强磁场中,磁感应强度大小为B=1.0T。一根与导轨等宽的金属棒ef垂直于MN、PQ静止
放置,且与导轨保持良好接触。金属棒质量m=0.1kg、电阻r=0.4Ω,距导轨底端S1=3.75m。
另一根与金属棒ef平行放置的绝缘棒gh长度也为d,质量为 ,从导轨最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑S2=0.2m后再次静止,此过程中电阻R上产生的电热为Q=0.2J。已知
,从导轨最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑S2=0.2m后再次静止,此过程中电阻R上产生的电热为Q=0.2J。已知
两棒与导轨间的动摩擦因数均为μ= ,g取10m/s2,求:
,g取10m/s2,求:
(1)绝缘棒gh与金属棒ef碰前瞬间绝缘棒的速率;
(2)两棒碰后,安培力对金属棒做的功以及碰后瞬间金属棒的加速度;
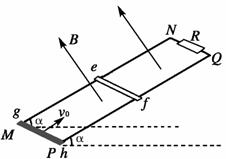 (3)金属棒在导轨上运动的时间。
(3)金属棒在导轨上运动的时间。
23.(18分)
如图所示,在绝缘的水平面上,相隔2L的AB两点固定有两个电量均为Q的正点电荷,C、O、D是AB连线上的三个点, O为连线的中点,CO=OD=。一质量为m、电量为q的带电物块以初速度v0从C点出发沿AB连线向B运动,运动过程中物块受到大小恒定的阻力作用,但在速度为零时,阻力也为零。当物块运动到O点时,物块的动能为初动能的n倍,到达D点刚好速度为零,然后返回做往复运动,直至最后静止在O点。已知静电力恒量为k,求:
(1)AB两处的点电荷在C点产生的电场强度的大小;
(2)物块在运动中受到的阻力的大小;
 (3)带电物块在电场中运动的总路程。
(3)带电物块在电场中运动的总路程。
22.(16分)
如图所示,在高1.25m的水平桌面上,一质量为2.0kg的物块在10N的水平拉力作用下,在A处由静止开始向桌边边缘B运动, 2s末撤去水平拉力。物块运动到桌面B端后飞出落在水平地面上。已知物块与桌面之间的动摩擦因数μ=0.3,AB之间的距离为6m,不计空气阻力,g=10m/s2。求:
 (1) 撤去水平拉力前物块加速度的大小;
(1) 撤去水平拉力前物块加速度的大小;
(2)物块离开桌面边缘B点时速度的大小;
(3)物块落地点距桌面边缘B点的水平距离。
24. (20分)把一个质量为m、带正电荷且电量为q的小物块m放在一个水平轨道的P点上,在轨道的O点有一面与轨道垂直的固定墙壁。轨道处于匀强电场中,电场强度的大小为E,其方向与轨道(ox轴)平行且方向向左。若把小物块m从静止状态开始释放,它能够沿着轨道滑动。已知小物体m与轨道之间的动摩擦因数恒为μ,P点到墙壁的距离为x。,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
(20分)把一个质量为m、带正电荷且电量为q的小物块m放在一个水平轨道的P点上,在轨道的O点有一面与轨道垂直的固定墙壁。轨道处于匀强电场中,电场强度的大小为E,其方向与轨道(ox轴)平行且方向向左。若把小物块m从静止状态开始释放,它能够沿着轨道滑动。已知小物体m与轨道之间的动摩擦因数恒为μ,P点到墙壁的距离为x。,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
(1)如果在P点把小物块从静止状态开始释放,那么它第1次撞墙之后瞬时速度为零的位置坐标x1、第2次撞墙之后速度为零的位置坐标x2的表达式分别是什么?
(2)如果在P点把小物块从静止状态开始释放,那么它最终会停留在什么位置?从开始到最后它一共走了多少路程(s)?
(3)如果在P点瞬间给小物块一个沿着x轴向右的初始冲量,其大小设为I,那么它第一次又回到P点时的速度(v1)大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程(s')?
22?(16分)
(1)小钢球经过C做平抛运动又回到A,在C的速度设为vC,空中飞行时间设为t,则:
在水平方向: x=vC t…………………………①
竖直方向上: 2R= gt2 ………………………②
gt2 ………………………②
解①②有: vC = …………………………③
…………………………③
(2)小钢球由B→C机械能守恒,所以有:
 m
m =
=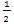 m
m +mg·2R……………………….④
+mg·2R……………………….④
∴ vB =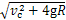 =
= …………⑤
…………⑤
(3)设在A点力F瞬间弹击小钢球的冲量大小为I,则应用动量定理有:
I=mvA ……………………………………… ⑥
由A到B小球做匀速直线运动,
∴ vA=vB………………………………………⑦
∴I=mvB=m  …………………..⑧
…………………..⑧
 23?(18分)
23?(18分)
(1)电子在复合场中二力平衡,即:
eE=evB……………………………①
∴ v=E/B……………………………②
(2)如图所示:其中r为电子在磁场中做圆(弧)运动的圆轨道半径。
所以:θ=π/2-α/2…………………③
tanθ=r/R…………………………④
又因:evB=m … ……………..……⑤
… ……………..……⑤
联解以上四式得: =
=  tan
tan ………⑥
………⑥
(3)还可以求出电子在磁场中做圆弧运动的圆半径r等(或指出:加速电场的电压U,等即可)
24?(18分)
由题意分析知,小物块m沿着轨道滑动时,水平方向上受到二力:滑动摩擦力f=μmg和电场力qE,而且总是有:qE>μmg……………………………..①
(1)设第一次速度为零的位置坐标为x1,取墙面为零电势面,则在这一运动过程中应用功能关系有:
μmgx0+μmgx1=qEx0-qEx1…………………………②
x1= x0 ……………………………………③
x0 ……………………………………③
设第二次速度为零的位置坐标为x2,取墙面为零电势面,则在第二次运动过程中应用功能关系有:
Μmgx1+μmgx2=qEx1-qEx2……………………④
x2= x1
x1
即:x2= 2x0…………………………………⑤
2x0…………………………………⑤
(2)它最终会停留在0点…………………………⑥
对从开始到最终的整个运动过程应用功能关系有:
μmgs=qEx0…………………………………………⑦
s=qE x0/μmg ……………………………………⑧
(3)由动量定理知,小物块获得一个向右的初始冲量I,那么向右运动的初速度:
v0=I/m……………………………………………⑨
设第一次瞬时速度为零的位置坐标为x1,取墙面为零电势面,则在这一运动过程中应用功能关系有:
μmg(x1-x0)=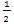 m
m -(qEx1-qEx0)………………⑩
-(qEx1-qEx0)………………⑩
得:x1= x0
x0
即:x1= x0 ………………… ⑩
x0 ………………… ⑩
同上道理, 对从开始到第一次又回到P点这一过程应用功能关系有:
2×μmg(x1-x0)=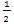 m
m -
- m
m
得:v1=
即:v1= … ………………………………(15).
… ………………………………(15).
小物块最终仍会停留在0点。
设从开始到最后一共走的路程为s′,全过程应用功能关系有:
μmgs′= qEx0+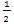 m
m
得:s′=
即:s′= …………………………?(17)
…………………………?(17)
崇文
23.(18分)下图为汤姆生在1897年测量阴极射线(电子)的荷质比时所用实验装置的示意图。K为阴极,A1和A2为连接在一起的中心空透的阳极,电子从阴极发出后被电场加速,只有运动方向与A1和A2的狭缝方向相同的电子才能通过,电子被加速后沿00’方向垂直进人方向互相垂直的电场、磁场的叠加区域。磁场方向垂直纸面向里,电场极板水平放置,电子在电场力和磁场力的共同作用下发生偏转。已知圆形磁场的半径为R,圆心为C。

某校物理实验小组的同学们利用该装置,进行了以下探究测量:
首先他们调节两种场强的大小:当电场强度的大小为E,磁感应强度的大小为B时,使得电子恰好能够在复合场区域内沿直线运动;然后撤去电场,保持磁场和电子的速度不变,使电子只在磁场力的作用下发生偏转,打在荧屏上出现一个亮点P,通过推算得到电子的偏转角为a(即: 与
与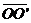 下之间的夹角)。若可以忽略电子在阴极K处的初速度,则:
下之间的夹角)。若可以忽略电子在阴极K处的初速度,则:
(1)电子在复合场中沿直线向右飞行的速度为多大?
(2)电子的比荷(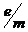 )为多大?
)为多大?
(3)利用上述已知条件,你还能再求出一个其它的量吗?若能,请指出这个量的名称。
22. (16分)如图所示,在光滑水平面右端B点处连接一个竖直的半径为R的光滑半圆形轨道BC,在距离B为x的A点,用一个较大的水平力向右瞬间弹击质量为m的小钢球,使其获得一个水平向右的初速度,质点到达B点后沿半圆形轨道运动,经过C点后在空中飞行,正好又落回到A点。 求:
(16分)如图所示,在光滑水平面右端B点处连接一个竖直的半径为R的光滑半圆形轨道BC,在距离B为x的A点,用一个较大的水平力向右瞬间弹击质量为m的小钢球,使其获得一个水平向右的初速度,质点到达B点后沿半圆形轨道运动,经过C点后在空中飞行,正好又落回到A点。 求:
(1)小钢球经过C时的速度有多大?
(2)小钢球经过B时的速度有多大?
(3)在A点,这个瞬间弹击小钢球的力的冲量需要有多大?
24.(20分)
解:(1)设此问题中弹簧的最大压缩量为x0,
则有  ①
①
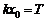 ②
②
解得  6分
6分
(2)由于小滑块压缩弹簧前的速度 大于(1)中所求的速度值v0,所以当弹簧的压缩量为x0时,小滑块的速度不为零。
大于(1)中所求的速度值v0,所以当弹簧的压缩量为x0时,小滑块的速度不为零。
设弹簧的压缩量为x0时,小滑块的速度为v,
有 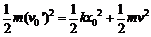 ③
③
由②③解得 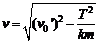 ④
④
此后细绳被拉断,木板与滑块(弹簧)组成的系统动量守恒,当弹簧的压缩量最大时,木板和小滑块具有共同速度,设共同速度为V
有
 ⑤
⑤
由④⑤解得 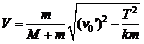 ⑥
8分
⑥
8分
(3)木板与小滑块通过弹簧作用完毕时,小滑块相对地面的速度应为0,设此时木板的速度为V1,并设小滑块压缩弹簧前的速度为 ,绳断瞬间小滑块的速度为 v,则有
,绳断瞬间小滑块的速度为 v,则有
 ⑦
⑦
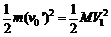 ⑧
⑧
由④⑦⑧解得小滑块最后离开木板时,相对地面速度为零的条件
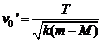 ,且
,且 6分
6分
宣武
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com