
题目列表(包括答案和解析)
3、(15分)(1) ;
; (2分)
(2分)
当夯杆与滚轮相对静止时: (2分)
(2分)
当夯杆以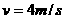 的初速度竖直上抛,上升高度为:
的初速度竖直上抛,上升高度为: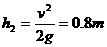 (2分)
(2分)
则当夯杆加速向上运动速度到达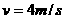 后,夯杆匀速上升,匀速上升高度为:
后,夯杆匀速上升,匀速上升高度为:
 (2分)
(2分)
因此,夯杆先匀加速上升,后匀速上升,再竖直上抛。 (1分)
故夯杆上升过程中被滚轮释放时的速度为4m/s;
此时夯杆底端离夯底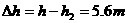 。 (2分)
。 (2分)
(2) (2分)
(2分)
(3)夯杆上抛运动的时间为: ; (1分)
; (1分)
夯杆匀速上升的时间为: ; (1分)
; (1分)
夯杆自由落体的时间为: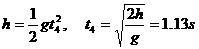 (1分)
(1分)
故打夯周期为: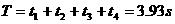 (1分)
(1分)
2、(12分)设斜面长为 ,高为
,高为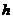 。有
。有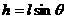
 (3分)
(3分)
已知: ,故有
,故有 (3分)
(3分)
根据动能定理:
 ,
,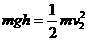 (3分)
(3分)
解得: (3分)
(3分)
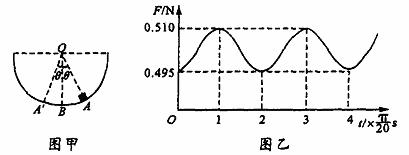
4、将一测力传感器连接到计算机上就可以测量快速变化的力,图甲表示小滑块(可视为质点)沿固定的光滑半球形容器内壁在竖直平面的A、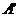 之间来回滑动,
之间来回滑动, 点与O点连线与竖直方向之间夹角相等且都为
点与O点连线与竖直方向之间夹角相等且都为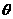 ,
,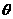 很小。图乙表示滑块对器壁的压力F随时间
很小。图乙表示滑块对器壁的压力F随时间 变化的曲线,且图中
变化的曲线,且图中 为滑块从A点开始运动的时刻,试根据力学规律和题中(包括图中)所给的信息,求:(1)小滑块的质量;(2)容器的半径;(3)滑块运动过程中的守恒量。(
为滑块从A点开始运动的时刻,试根据力学规律和题中(包括图中)所给的信息,求:(1)小滑块的质量;(2)容器的半径;(3)滑块运动过程中的守恒量。( 取
取 )
)
|
1 |
 |
 |
3、图示是建筑工地常用的一种“深穴打夯机”。工作时,电动机带动两个紧压夯杆的滚轮匀速转运将夯杆从深为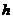 的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯在自身重力作用下,落回深坑,夯实坑底。然后,两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作。已知两个滚轮边缘线速度
的坑中提上来,当两个滚轮彼此分开时,夯杆被释放,最后夯在自身重力作用下,落回深坑,夯实坑底。然后,两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作。已知两个滚轮边缘线速度 恒为
恒为 ,每个滚轮对夯杆的正压力
,每个滚轮对夯杆的正压力 为
为 ,滚轮与夯杆间的动摩擦因数
,滚轮与夯杆间的动摩擦因数 为0.3,夯杆质量
为0.3,夯杆质量 为
为 ,坑深
,坑深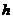 为6.4m。假定在打夯的过程中坑的深度变化不大,且夯杆底端升到坑口时,速度正好为零。取
为6.4m。假定在打夯的过程中坑的深度变化不大,且夯杆底端升到坑口时,速度正好为零。取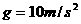 。求:
。求:
(1)夯杆上升过程中被滚轮释放时的速度为多大,此时夯杆底端离夯底多高;
(2)每个打夯周期中,电动机对夯杆所作的功;
(3)打夯周期。

2、如图所示,物体从倾角为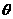 的斜面顶端由静止沿斜面滑下,它滑到底端的速度是它从同样高度自由下落的速度的k倍(k<1),则物体沿斜面下滑时间t1与自由落体时间t2之比为多少,物体与斜面的摩擦系数为多大。
的斜面顶端由静止沿斜面滑下,它滑到底端的速度是它从同样高度自由下落的速度的k倍(k<1),则物体沿斜面下滑时间t1与自由落体时间t2之比为多少,物体与斜面的摩擦系数为多大。

1、一个小球从倾角为37°的斜面上O点以初速v0水平抛出,落在斜面上A点,如图所示。小球抛出后经过时间 时,离斜面最远。若第二次以水平速度v0’。从同一位置同方向抛出,小球落在斜面上B点,两次落至斜面时的动能与抛出时动能相比,其增量之比
时,离斜面最远。若第二次以水平速度v0’。从同一位置同方向抛出,小球落在斜面上B点,两次落至斜面时的动能与抛出时动能相比,其增量之比 ,则两次抛出时的初速度大小之比为
,则两次抛出时的初速度大小之比为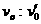 =___________。
=___________。

13.由机械能守恒定律,B球通过圆管最高点时的速度v满足方程:1/2m2v2+m2g2R=1/2m2v02对于A球,N1-mg=m1v02/R 对于B球,N2 + m2g = m2v2/R又N1 = N2,解得(m1-m2)v0/R + (m1 + 5m2)g = 0.
12.
 设绳与竖直方向夹角为θ,则cosθ = mg/T = 1/2,所以θ=60о,小球在绳断时离地高度为:h = H - Lcosθ.小球做匀速圆周运动的半径为:r = Lsinθ,F向=m等 mv2/r mgtanθ+1/2mv2 = mg(H-L/2)
+1/2mv2 求得:H=3.3 m,平抛运动时间为:t = 2g/h
= 0.6 s,水平距离为:s =
v0t =√16.2m,圆柱半径为:R = √s2+r2 = 4.8 m.
设绳与竖直方向夹角为θ,则cosθ = mg/T = 1/2,所以θ=60о,小球在绳断时离地高度为:h = H - Lcosθ.小球做匀速圆周运动的半径为:r = Lsinθ,F向=m等 mv2/r mgtanθ+1/2mv2 = mg(H-L/2)
+1/2mv2 求得:H=3.3 m,平抛运动时间为:t = 2g/h
= 0.6 s,水平距离为:s =
v0t =√16.2m,圆柱半径为:R = √s2+r2 = 4.8 m.
11. 要使B静止.A必须相对于转盘静止,因此具有与转盘相同的角速度,A需要的向心力由绳拉力和静摩擦力合成.角速度取最大值时,A有离心趋势,静摩擦力指向圆心O;角速度取最小值时,A有向心运动的趋势,静摩擦力背离圆心O.对于B,T = mg对于A,T + F = mrw12,T–F = mrw22,解得:w1 = 6.5rad/s,w2 =2.9rad/s,所以2.9 rad/s< w <6.5rad/s.
10. L = l0/2 + √l02/4-lv2/g
L = l0/2 + √l02/4-lv2/g
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com