1．下列物理量的单位中属于国际单位制中基本单位的是

A．焦耳　　　　　　　　　　　 B．牛顿　　　　　　　　　　　 C．特斯拉　　　　　　　　　 D．开尔文

15．(16分)如图所示，直线MN的下方有竖直向下的匀强电场，场强大小为E=700V/m。在电场区域内有一个平行于MN的挡板PQ；MN的上方有一个半径为R=0.866m的圆形弹性围栏，在围栏区域内有图示方向的匀强磁场，磁感应强度大小为B=1.4T。围栏最低点一个小洞b，在b点正下方的电场区域内有一点a，a点到MN的距离d₁=45cm，到PQ距离d₂=5cm。现将一个质量为m=0.1g ，带电量q=2×10^-3C的带正电小球(重力不计)，从a点由静止释放，在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍，且碰撞前后瞬间小球的动能不变，不计小球运动过程中的空气阻力以及小球与围栏碰撞时的能量损失，试求：(已知，)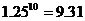

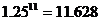⑴求出小球第一次与挡板PQ相碰后向上运动的距离；

⑵小球第一次从小洞b进入围栏时的速度大小；

⑶小球从第一次进入围栏到离开围栏经历的时间。

解析：

⑴设小球第一次与挡板相碰后向上运动距离为x₁，则

qEd₂ =0.8qEx₁　　　 　(2分)

x₁=1.25d₂=6.25(cm)　　 　(2分)

⑵设第n次与挡板PQ相碰后向上运动距离为x_n，则：

　　　 　(2分)

要使小球能进入围栏，应有：

x_n>d₁+d₂　 　　　　　　

综上：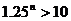　

所以：当小球与挡板碰撞11次后，小球将第一次进入围栏内　 　(2分)

设进入速度大小为v，则应有：

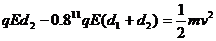　 　(2分)

解得：v=14(m/s)　　 　　(1分)

⑶小球进入圆形围栏后，在洛伦兹力作用下做匀速圆周运动，如图所示

　 　　所以轨道半径 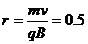(m) 　　(2分)

运动周期 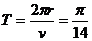(s) 　　

图中 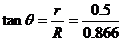　所以 θ=30° 　　　　　(2分)

即，当小球每转过120°圆周就与围栏碰撞一次，最终经过5次碰撞，从小洞b离开围栏区，故在围栏内运动时间为：

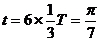(s) 　　　　　　(1分)

14．(16分)如图所示，竖直放置的足够长平行光滑金属导轨ab、cd，处在垂直导轨平面向里的水平匀强磁场中，其上端连接一个阻值为R=0.40Ω的电阻；质量为m=0.01kg、电阻为r=0.30Ω的金属棒MN紧贴在导轨上，保持良好接触。现使金属棒MN由静止开始下滑，通过位移传感器测出下滑的位移大小与时间的关系如下表所示，导轨电阻不计，重力加速度g取l0m/s²。试求

⑴当t=1.0s瞬间，电阻R两端电压U大小；

⑵金属棒MN在开始运动的前1s内，电阻R上产生的热量；

⑶从开始运动到t=1.0s的时间内，通过电阻R的电量。

解析：

⑴从位移与时间关系数据可知，从0.8s以后，金属棒MN已经做匀速运动，速度大小为v_m=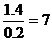(m/s)　　　　　　 (2分)

又当匀速运动时，应有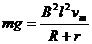：　　　　 (2分)

所以Bl=0.1　　　　 (1分)

故在t=1.0s瞬间，电阻R两端电压U=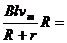0.4(V)　　　　 (2分)

⑵金属棒MN下滑1s的过程中，由动能定理

mgx-W_安=　　　 (3分)

所以 W_安=0.158(J)　　 (1分)

电阻R上产生的热量为Q=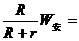0.09(J)　　 (1分)

⑶通过电阻R的电量为

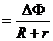
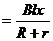　　　　 (2分)

　　　 (2分)

13．(15分)如图甲所示，长为4m的水平轨道AB与半径为R=0.6m的竖直半圆弧轨道BC在B处相连接，有一质量为1kg的滑块(大小不计)，从A处由静止开始受水平向右的力F作用，F的大小随位移变化关系如图乙所示，滑块与AB间动摩擦因数为0.25，与BC间的动摩擦因数未知，取g =l0m/s²。求：

⑴滑块到达B处时的速度大小；

⑵滑块在水平轨道AB上运动前2m过程中所需的时间；

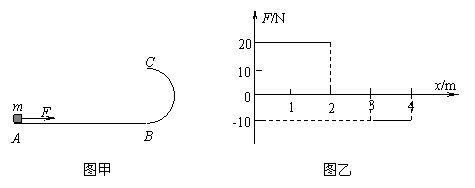⑶若滑块到达B点时撤去力F，滑块沿半圆弧轨道内侧上滑，并恰好能达到最高点C，则滑块在半圆轨道上克服摩擦力所做的功是多少。

解析：

⑴滑块从A到B的过程中，由动能定理

　F₁x₁－F₂x₃－μmgx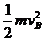＝　(3分)

即 20×2-10×1-0.25×1×10×4=

得：v_B=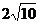(m/s)　 　(2分)

⑵在前2m内：F₁-μmg＝ma₁

　　　　 且　 x₁=　　 　(2分)

解得：t₁=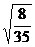　 (s)　 　(2分)

　 ⑶当滑块恰好能到达C点时，应有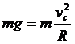：　 　(2分)

　 滑块从B到C的过程中，由动能定理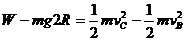：　 　(2分)

得：W=-5(J) 即克服摩擦力做功为5J。　 　(2分)

12．[选做题]本题包括A、B、C三小题，请选定其中两题，并在相应的答题区域内作答。若三题都做，则按A、B两题评分．

A．(模块3-3)(12分)

⑴下列说法正确的是(　　　 )

A．只要外界对气体做功，气体内能一定 增大

B．物体由气态变成液态的过程，分子势能减小

C．当分子间距离增大时，分子间引力增大，而分子间斥力减小

D．液体表面层的分子比液体内部的分子有更大的分子势能

⑵如图所示，弹簧一端固定于水平面上，另一端与质量为m的活塞拴接在一起，开口向下、质量为M的气缸与活塞一起封闭了一定质量的气体。气缸和活塞均可与外界进行热交换。若外界环境的温度缓慢降低，则封闭气体的体积将　　　 　(填“增大”、“减小”或“不变”)，同时将　 　　　　(填“吸热”、“放热”或“既不吸热，也不放热”)。

⑶某种油的密度为，摩尔质量为M。取体积为V的油慢慢滴出，可滴n滴。将其中一滴滴在广阔水面上，形成面积为S的单分子油膜。试估算：①阿伏加德罗常数；②其中一滴油滴含有的分子数．

解析：⑴BD　 (4分)

⑵减小　 (2分)；　 放热(2分)

⑶①油分子的直径为：　　　　 一摩尔油的体积为：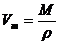

所以阿伏加德罗常数为：　 (2分)(注：本题也可以用立方体模型求解)

②一滴油含有的分子数为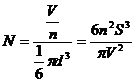：　　 (2分)

B．(选修3-4模块)(12分)

⑴以下说法正确的是　　 　(　　 )

A．狭义相对论两个基本假设之一是在不同惯性参考系中，一切物理定律都是相同的

B．变化的电场不一定能产生出变化的磁场

C．如果质点所受合外力总是指向平衡位置，质点的运动就是简谐运动

D．在波的干涉中，振动加强的点一定处在波峰或波谷的叠加处

⑵两个同学利用假期分别去参观北京大学和南京大学的物理实验室，各自在那里利用先进的DIS系统较准确地探究了“单摆的周期T与摆长L的关系”，他们通过校园网交换实验数据，并由计算机绘制了T²-L图象，如图甲所示．去北大的同学所测实验结果对应的图线是　 　　(选填“A”或“B”)。另外，在南大做探究的同学还利用计算机绘制了两种单摆的振动图象(如图乙)，由图可知，两单摆摆长之比　　 　　。

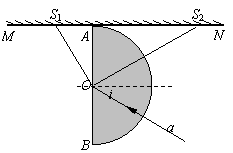
⑶图所示，半圆玻璃砖的半径R=10cm，折射率为n=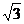，直径AB与屏幕垂直并接触于A点。激光a以入射角i=30°射向半圆玻璃砖的圆心O，结果在水平屏幕MN上出现两个光斑。求两个光斑之间的距离L。

解析：

⑴AB　　 (4分)

⑵B　　 (2分)；　 (2分)

⑶光路如右图所示，两个光斑S_1­、S₂之间的距离为

　 (cm)　　　 (4分)

C．(选修3-5)(12分)

⑴以下说法正确的是　　　　　 (　　 )

A．X射线是处于激发态的原子核辐射出的

B．比结合能越大，表示原子核中核子结合得越牢靠，原子核越稳定

C．放射性元素发生一次β衰变，原子序数增加1

D．当氢原子从n=3的状态跃迁到n=2的状态时，核外电子的运动加速度减小

⑵如图所示的实验电路，当用黄光照射光电管中的金属涂层时，毫安表的指针发生了偏转．若将电路中的滑动变阻器的滑片P向右移动到某一位置时，毫安表的读数恰好减小到零，此时电压表读数为U。

①若增加黄光照射的强度，则毫安表　　 (选填“有”或“无”)示数。

②若改用蓝光照射光电管中的金属涂层，则毫安表 　　(选填“有”或“无”)示数。

⑶一质量为M的航天器远离太阳和行星，正以速度v₀在太空中飞行，某一时刻航天器接到加速的指令后，发动机瞬间向后喷出质量为m的气体，气体向后喷出的速度大小为v₁，求加速后航天器的速度大小。(v₀ 、v₁均为相对同一参考系的速度)

解析：

⑴BC (4分)

⑵ ①无　 (2分)　 　②有　 (2分)

⑶设速度v₀的方向为正方向，则由动量守恒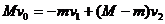：　 　　　　　(2分)

所以，加速后航天器的速度大小：　　　 (2分)

11．(10分)在“测定金属导体的电阻率”的实验中，待测金属导线的电阻R_x 约为3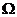。实验室备有下列实验器材

A．电压表V₁(量程3V，内阻约为15K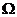)　　　　　　 B．电压表V₂ (量程15V，内阻约为75K)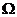

C．电流表A₁(量程3A，内阻约为0.2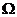)　　　　　　　 D．电流表A₂(量程600mA，内阻约为1)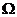

E．变阻器R₁ (0-10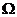，1.0A)　　　　　　　　　　　 F．变阻器R₂ (0~100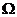，0.3 A)

G．电池E(电动势为3V，内阻约为0.3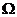)　　　　　　 H．开关S，导线若干

⑴提高实验精确度，减小实验误差，应选用的实验器材有　　　　　　　　 　。

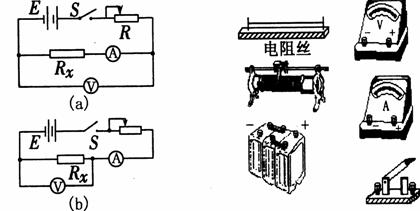⑵为了减小实验误差，应选用下图中　　　　　 (填“a”或“b”)为该实验的电原理图，并按所选择的原理图把实物图用导线连接起来。

⑶用刻度尺测得金属丝长度为60.00cm，用螺旋测微器测得导线的直径为0.635mm，两电表的示数分别如下图所示，则电阻值为　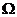　　 ，电阻率为　　　 ___________。

解答：

⑴ADEGH(2分)

⑵b (2分)　　　 连图略(3分)

⑶2.4Ω(1分)　　 1.3×10^-6Ω·m(2分)

[必做题]

10．(8分)物体因绕轴转动时而具有的动能叫转动动能。某同学为探究转动动能的大小与角速度大小的关系，设计了如下实验：先让砂轮由电动机带动做匀速转动并测出其角速度ω，然后让砂轮脱离动力，由于克服轮边缘的摩擦阻力做功(设阻力大小不变)，砂轮最后停下，测出砂轮开始脱离动力到停止转动的圈数n，实验中得到几组n和ω的数值如下表。(已知砂轮直径d=10cm，轮边缘所受阻力大小为0.3N)

⑴先算出砂轮不同转速对应的转动动能，填在上述表格中；

⑵选择适当的物理量在坐标纸上作出能直观反映转动动能与角速度关系的图象，根据图象写出砂轮的转动动能E_k与角速度ω的定量关系是　　 　　　。

解答：⑴(3分)

⑵如下图所示

作图3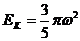分；　 　2分

9．ACD

解析：当d =l时，线框移动时的磁通量始终不变，故无感应电流，A正确；当d =l/2时，线框的MN边位于x = l处瞬间，MN、PQ所在处磁场为零，感应电动势为零，而在l/2处时，磁场最大，所以感应电动势最大，B错误，C正确。

9．一个矩形金属框MNPQ置于xOy平面内，平行于x轴的边NP的长为d，如图(a)所示。空间存在磁场，该磁场的方向垂直于金属框平面，磁感应强度B沿x轴方向按图(b)所示正弦规律分布，x坐标相同各点的磁感应强度相同。当金属框以大小为v的速度沿x轴正方向匀速运动时，下列判断正确的是

A．若d =l，则线框中始终没有感应电流

B．若d = l/2，则当线框的MN边位于x = l处时，线框中的感应电流最大

C．若d = l/2，则当线框的MN边位于x = l/4处时，线框受到的安培力的合力最大

D．若d = 3l/2，则线框中感应电流周期性变化的周期为l/v

8．AC

解析：当滑动触头向右移动时，加速电压变大，进入偏转磁场时的速度变大，因此，轨道半径变大，所以打在荧光屏上时的位置上升，同时在磁场中的圆弧对应圆心角变小，即运动时间变短，A正确，B错误；因洛伦兹力不做功，所以只改变磁场时，电子的速度不变，C正确，D错误。