
题目列表(包括答案和解析)
30.(22分)果蝇是遗传学研究的好材料,人们对果蝇的遗传及变异作了较充分的研究。
问题一:早在人类基因组计划之前,人们就已经对果蝇的的基因组进行了测序,如累你是研究人员,你认为应测果蝇的几条染色体DNA? 。
问题二:人们研究发现,Y染色体含有几十个基因。如果果蝇的刚毛、截毛这对相对性状由X、Y染色体上的一对等位基因控制,刚毛基因B对截毛基因b为显性。让刚毛果蝇与截毛果蝇杂交,后代中,雌果蝇全为刚毛,雄果蝇全为截毛,则亲本的杂交组合为(基因型): 。用遗传学图解表示这一杂交过程。
问题三:某生物兴趣小组饲养了一批纯合的长翅红眼果蝇幼虫,分装在10支试管中,准备放在25℃培养箱中培养(果蝇生长的最适温度),由于疏忽,其中有2支试管未放入培养箱,当时气温高达37℃,十天后观察发现,培养箱中的果蝇全为长翘,而未放人培养箱中的果蝇出现残翅。
(1)残翅性状的出现在遗传学上称为 。你认为出现残翅的最可能的原因是 。
(2)请设计实验证明你的推测。(简要写出实验步骤,预期结果并得出结论。提示:选择果蝇杂交的方法进行实验)
实验步骤:a.
b.
c.
预期结果与结论:
5.用黄色短杆菌生产赖氨酸,有关叙述正确的是:
A.对黄色短杆菌进行诱变处理.可获得大量积累赖氨酸的高产菌株
B.在稳定期,活菌数稳定,赖氨酸的产量也不再增加
C.发酵过程中.可以向发醇罐中通入空气并搅拌,以增加溶氧,提高原料的利用率
D.赖氨酸是黄色短杆菌的次级代谢产物
4.下列有关生态学问题的表述正确的是:
A.种植玉米时,因玉米高矮不一,具有分层现象,所以要合理密植。
B.生态系统的成分包括生产者、消费者和分解者,三者紧密联系、缺一不可。
C.对某生态系统中某种乔木取样调查,选取5个合适样方.各样方面积为S(rn2),记数的结果分别是nl、n2、n3、n4、n5,刖该乔木的种群密度为(nl+n2+n3+n4+n5)/5S(株/rn2)
D.若流入初级消费者、次级消费者、三级消费者的能量依次为Q1、Q2、Q3,则Q1≥Q2+Q3
3.癌症是威胁人类健康的一类重要疾病。人们对它进行了大量的研究,以下是有关癌细胞结构及生理的描述。你认为正确的是:
①每个癌细胞都有数目相同的染色体组 ②新陈代谢速度减慢,细胞萎缩
③每个癌细胞的DNA量不一定相等 ④都具有两个中心体,且分别位于细胞的两极
⑤在某些病毒的诱导下能产生原癌基因 ⑥细胞内的色素逐渐积累
⑦失去控制.无限增殖
A.①⑦ B.②④ C.⑤⑥ D.③⑦
2.下面为DNA测序仪显示的某真核生物DNA片段一条链的碱基排列,其顺序为GGTTATGCGT,下列及相关问题的回答锖误的是:
A.第二链的碱基排列顺序是CCAATACGCA
B.若将此真核生物的基因导入细菌,在获取该基因时最好采用“鸟枪法”
C.该DNA片段中(A+C)/(T+G)=1
D.如果该DNA分子为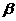 一珠蛋白的DNA探针,则可用它来检测镰刀型细胞贫血症
一珠蛋白的DNA探针,则可用它来检测镰刀型细胞贫血症
1.利用细胞工程方法,以SARS病毒核衣壳蛋白为抗原制备出单克隆抗体。下列相关叙述正确的是
A.用纯化的核衣壳蛋白反复注射到小鼠体内,产生的血清抗体为单克隆抗体
B.体外培养单个效应B细胞可以获得大量针对SARS病毒的单克隆抗体
C.将等量效应B细胞和量髓瘤细胞混合,经PEG诱导融合后的细胞不一定为杂交瘤细胞
D.利用该单克隆抗体与SARS病毒核衣壳蛋白特异性结合的方法不一定诊断出SARS病毒感染者
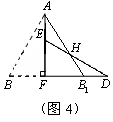
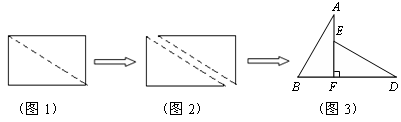
26.小明将一张矩形纸片沿对角线剪开,得到两张全等直角三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,使点B、F、D在同一条直线上,F为公共直角顶点。然后小明又将图(3)中的△ABF沿直线AF翻折到图(4)的位置,点B落在FD边上的B1点,AB1交DE于点H。
请你说明:(1)AH=DH.;(2)点H在∠AFD的角平分线上。
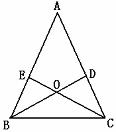
25.如图,在△ABC中, D、E分别是AC、AB上的点, BD与CE交于点O. 给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.
(1)上述三个条件中, 哪两个条件可判定△ABC是等腰三角形(用序号写出所有情形);
(2)选择第⑴小题中的一种情形, 证明△ABC是等腰三角形.
24.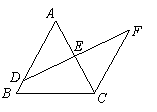 如图,在
如图,在 中,
中,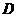 是
是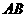 上一点,
上一点,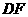 交
交 于点
于点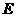 ,
,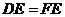 ,
,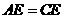 ,
,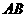 与
与 有什么位置关系?证明你的结论.
有什么位置关系?证明你的结论.
23.如图,在平面直角坐标系中,直线L是第一、三象限两坐标轴夹角的角平分线.
(1)由图观察易知A(0,2)关于直线L的对称点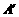 的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5)
关于直线l的对称点
的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5)
关于直线l的对称点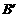 、
、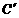 的位置,并写出他们的坐标:
的位置,并写出他们的坐标:
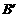 、
、 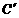 ;
;
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限两坐标轴角平分线L的对称点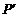 的坐标为
(不必证明);
的坐标为
(不必证明);
 (3)已知两点D(x, y)、E(
(3)已知两点D(x, y)、E(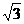 -1, 1-3
-1, 1-3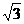 ),关于第一、三象限两坐标轴夹角平分线对称,
),关于第一、三象限两坐标轴夹角平分线对称,
那么x+3y=
(4)请你猜测:坐标平面内任一点Q(m,n)
关于第二、四象限两坐标轴角平分线
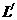 的对称点
的对称点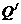 的坐标为
的坐标为
(不必证明);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com