
题目列表(包括答案和解析)
7.满足不等式组 的点
的点 的集合的面积是( ▲ )
的集合的面积是( ▲ )
A. B.
B.  C.
C.
 D.
D.

6.已知点
 是圆
是圆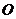 :
: 内一点,直线
内一点,直线 是以
是以 为中点的弦所在的直线,若直线
为中点的弦所在的直线,若直线 的方程为
的方程为 ,则( ▲ )
,则( ▲ )
A.  与
与 重合且
重合且 与圆
与圆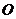 相离
B.
相离
B.  ⊥
⊥ 且
且 与圆
与圆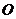 相离
相离
C.  ∥
∥ 且
且 与圆
与圆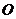 相交
D.
相交
D.  ∥
∥ 且
且 与圆
与圆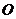 相离
相离
5、下图代表未折叠正方体的展开图,将其折叠起来,变成正方体后的图形是( ▲ )

A. B. C. D.
4.已知等比数列 中,
中, ,
, ,则前9项之和等于( ▲ )
,则前9项之和等于( ▲ )
A.50 B.70 C.80 D.90
3. 复数 是实数,则实数
是实数,则实数 的值为( ▲ )
的值为( ▲ )
A.-1
B.0
C.1
D.
2.设x是实数,则“x>0”是“|x|>0”的( ▲ )
A.充分不必要条件 B. 必要不充分条件 C.充要条件 D.既不充分也不必要条件
1.  全集U=R,
全集U=R, ,
, ,则图中
,则图中
阴影表示的集合为( ▲)
A. B.
B. C.
C. D.
D.
12、解:(Ⅰ)椭圆 的方程
的方程 ……3分
……3分
(Ⅱ)(1) ,设
,设 边上的高为
边上的高为 ,
,
设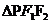 的内切圆的半径为
的内切圆的半径为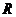 ,因为
,因为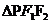 的周长为定值6.所以
的周长为定值6.所以  ……5分
……5分
当P在椭圆上顶点时, 最大为
最大为 ,
,
 故
故  的最大值为
的最大值为 ,
,
于是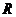 也随之最大值为
也随之最大值为
此时内切圆圆心的坐标为 ……7分
……7分
(2)将直线 代入椭圆
代入椭圆 的方程
的方程 并整理.
并整理.
得 .设直线
.设直线 与椭圆
与椭圆 的C交点
的C交点 ,
,
由根系数的关系,得 .
……9分
.
……9分
直线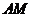 的方程为:
的方程为: ,它与直线
,它与直线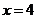 的交点坐标为
的交点坐标为
 同理可求得直线
同理可求得直线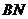 与直线
与直线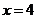 的交点坐标为
的交点坐标为 .…11分
.…11分
下面证明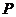 、
、 两点重合,即证明
两点重合,即证明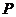 、
、 两点的纵坐标相等:
两点的纵坐标相等:
 ,
,

因此结论成立. 综上可知.直线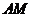 与直线
与直线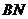 的交点住直线
的交点住直线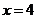 上. ……………13分
上. ……………13分
海淀区高三年级第二学期期末练习(理科)
解:(Ⅰ)由题意,抛物线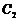 的方程为:
的方程为: ,……2分
,……2分
(Ⅱ)设直线 的方程为:
的方程为: .
.
 联立
联立 ,消去
,消去 ,得
,得  ,
,
………………3分
显然 ,设
,设 ,
,
则  ①
①  ② ……4分
② ……4分
又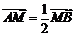 ,所以
,所以  ③ ………………5分
③ ………………5分
由①② ③消去 ,得
,得  ,
,
故直线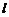 的方程为
的方程为 或
或 .
…………………6分
.
…………………6分
(Ⅲ)设 ,则
,则 中点为
中点为 , 因为
, 因为 两点关于直线
两点关于直线 对称,
对称,
所以 ,即
,即 ,解之得
,解之得 , …………………8分
, …………………8分
将其代入抛物线方程,得 ,所以,
,所以, . ……9分
. ……9分
联立  ,消去
,消去 ,得:
,得: . ……10分
. ……10分
由 ,得
,得 ,
,
即 ,……12分
,……12分
将 ,
, 代入上式并化简,得
代入上式并化简,得
 ,所以
,所以 ,即
,即 ,因此,椭圆
,因此,椭圆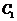 长轴长的最小值为
长轴长的最小值为 .
.
11.解:(Ⅰ)由已知 ,
, 

 ,两边取对数得
,两边取对数得  ,即
,即
 是公比为2的等比数列.
是公比为2的等比数列.
(Ⅱ)当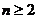 时,
时, 展开整理得:
展开整理得: ,若
,若 ,则有
,则有 ,则
,则 矛盾,所以
矛盾,所以 ,所以在等式两侧同除以
,所以在等式两侧同除以 得
得 ,
, 为等差数列
为等差数列 
(Ⅲ)由(Ⅰ)知




 =
=


 www.k
www.k
10.解:(Ⅰ)
 …………………………………………2分
…………………………………………2分
列表得 …………………………………………
………………………………………… 5分
5分
( Ⅱ)
Ⅱ) 在区间
在区间 上
上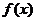 的图象恒在
的图象恒在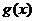 图象的上方
图象的上方
 在
在 上恒成立得
上恒成立得 在
在 上恒成立…………7分
上恒成立…………7分
设
 则
则

 ………………………9分
………………………9分
 …………………………………………10分
…………………………………………10分
(3)因 最大值
最大值
 ①当
①当 时,
时,

②当 时,
时, (ⅰ)当
(ⅰ)当

(ⅱ)当 时,
时, 在
在 单调递增;
单调递增;
1°当 时,
时,


 ;
;
2°当
(ⅰ)当
(ⅱ)当

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com