24、(2011•綦江县)如图，等边△ABC中，AO是∠BAC的角平分线，D为AO上一点，以CD为一边且在CD下方作等边△CDE，连接BE．

(1)求证：△ACD≌△BCE；

(2)延长BE至Q，P为BQ上一点，连接CP、CQ使CP=CQ=5，若BC=8时，求PQ的长．

考点：全等三角形的判定与性质；等边三角形的性质；含30度角的直角三角形；勾股定理。

分析：(1)由△ABC与△DCE是等边三角形，可得AC=BC，DC=EC，∠ACB=∠DCE=60°，又由∠ACD+∠DCB=∠ECB+∠DCB=60°，即可证得∠ACD=∠BCE，所以根据SAS即可证得△ACD≌△BCE；

(2)首先过点C作CH⊥BQ于H，由等边三角形的性质，即可求得∠DAC=30°，则根据等腰三角形与直角三角形中的勾股定理即可求得PQ的长．

解答：解：(1)∵△ABC与△DCE是等边三角形，

∴AC=BC，DC=EC，∠ACB=∠DCE=60°，

∴∠ACD+∠DCB=∠ECB+∠DCB=60°，

∴∠ACD=∠BCE，

∴△ACD≌△BCE(SAS)；

(2)过点C作CH⊥BQ于H，

∵△ABC是等边三角形，AO是角平分线，

∴∠DAC=30°，

∵△ACD≌△BCE，

∴∠QBC=∠DAC=30°，

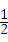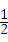∴CH=BC=×8=4，

∵PC=CQ=5，CH=4，

∴PH=QH=3，

∴PQ=6．

点评：此题考查了全等三角形的判定与性质，等腰三角形、等边三角形以及直角三角形的性质等知识．此题综合性较强，但难度不大，解题时要注意数形结合思想的应用．

23、(2011•綦江县)如图，已知A (4，a)，B (﹣2，﹣4)是一次函数y=kx+b的图象和反比例函数y=﹣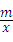的图象的交点．

(1)求反比例函数和一次函数的解祈式；

(2)求△A0B的面积．

考点：反比例函数与一次函数的交点问题。

专题：几何图形问题；数形结合。

分析：(1)A (4，a)，B (﹣2，﹣4)两点在反比例函数y=﹣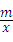的图象上，则由m=xy，得4a=(﹣2)×(﹣4)=m，可求a、m的值，再将A、B两点坐标代入y=kx+b中求k、b的值即可；

(2)设直线AB交y轴于C点，由直线AB的解析式求C点坐标，根据S_△AOB=S_△AOC+S_△BOC求面积．

解答：解：(1)将A (4，a)，B (﹣2，﹣4)两点坐标代入y=﹣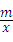中，得4a=(﹣2)×(﹣4)=m，

解得a=2，m=8，

将A(4，2)，B(﹣2，﹣4)代入y=kx+b中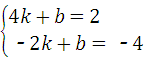，得，解得，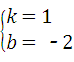

∴反比例函数解析式为y=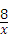，一次函数的解祈式为y=x﹣2；

(2)设直线AB交y轴于C点，

由直线AB的解析式y=x﹣2得C(0，﹣2)，

∴S_△AOB=S_△AOC+S_△BOC=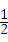×2×4+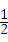×2×2=6．

点评：本题主要考查了待定系数法求反比例函数与一次函数的解析式．运用数形结合的方法求图形的面积，做此类题要根据图形的特点，将所求三角形的面积问题划分为两个三角形求解．

22、(2011•綦江县)我县实施新课程改革后，学习的自主字习、合作交流能力有很大提高，张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半个月的跟踪调査，并将调査结果分成四类，A：特别好；B：好；C：一般；D：较差；并将调査结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：

(1)本次调查中，张老师一共调査了　20　名同学，其中C类女生有　2　名，D类男生有　1　名；

(2)将上面的条形统计图补充完整；

(3)为了共同进步，张老师想从被调査的A类和D类学生中分别选取一位同学迸行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．

考点：条形统计图；扇形统计图；列表法与树状图法。

分析：(1)由扇形统计图可知，特别好的占总数的15%，人数有条形图可知3人，所以调查的样本容量是：3÷15%，即可得出C类女生和D类男生人数；

(2)根据(1)中所求数据得出条形图的高度即可；

(3)根据被调査的A类和D类学生男女生人数列表即可得出答案．

解答：解：(1)3÷15%=20，

20×25%=5．女生：5﹣3=2，

1﹣25%﹣50%﹣15%=10%，

20×10%=2，男生：2﹣1=1，

故答案为：20，2，1；

(2)如图所示：

(3)根据张老师想从被调査的A类和D类学生中分别选取一位同学迸行“一帮一”互助学习，可以将A类与D类学生分为以下几种情况：

利用图表可知所选两位同学恰好是一位男同学和一位女同学的概率为：

=．

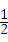点评：此题主要考查了条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．

21、(2011•綦江县)先化简，再求值：，其中x=．

考点：分式的化简求值。

专题：计算题。

分析：先根据分式混合运算的法则把原式化简，再把x=代入进行计算即可．

解答：解：原式=÷，

=×，

=，

当x=时，原式=，

=．

点评：本题考查的是分式的化简求出，熟知分式混合运算的法则是解答此题的关键．

20、(2011•綦江县)如图，小刚同学在綦江南州广场上观测新华书店楼房墙上的电子屏幕CD，点A是小刚的眼睛，测得屏幕下端D处的仰角为30°，然后他正对屏幕方向前进了6米到达B处，又测得该屏幕上端C处的仰角为45°，延长AB与楼房垂直相交于点E，测得BE=21米，请你帮小刚求出该屏幕上端与下端之间的距离CD．(结果保留根号)

考点：解直角三角形的应用-仰角俯角问题。

专题：应用题。

分析：易得CE=BE，利用30°的正切值即可求得CE长，进而可求得DE长．CE减去DE长即为广告屏幕上端与下端之间的距离．

解答：解：∵∠CBE=45°，CE⊥AE，

∴CE=BE．

∴CE=21，

∴AE=AB+BE=21+6=27．

在Rt△ADE中，∠DAE=30°，

∴DE=AE×tan30°=27×=9，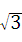

∴CD=CE﹣DE=21﹣9．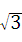

答：广告屏幕上端与下端之间的距离约为21﹣9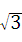m．

点评：本题考查了仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形；难点是充分找到并运用题中相等的线段．

19、(2011•綦江县)为了推进农村新型合作医疗制度改革，准备在某镇新建一个医疗点P，使P到该镇所属A村、B村、C村的村委会所在地的距离都相等(A、B、C不在同一直线上，地理位置如下图)，请你用尺规作图的方法确定点P的位置．

要求：写出已知、求作；不写作法，保留作图痕迹．

考点：作图-应用与设计作图。

分析：根据垂直平分线的性质得出，两垂直平分线的交点即是所求答案．

解答：解：已知A村、B村、C村，

求作新建一个医疗点P，使P到该镇所属A村、B村、C村的村委会所在地的距离都相等；

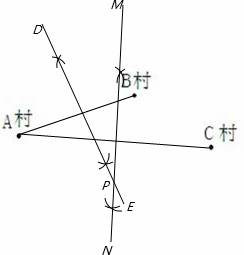
点评：此题主要考查了垂直平分线的性质，做出垂直平分线的性质得出是解决问题的关键．

18、(2011•綦江县)解方程：．

考点：解分式方程。

专题：计算题。

分析：观察分式方程的两分母，得到分式方程的最简公分母为(x﹣3)(x+1)，在方程两边都乘以最简公分母后，转化为整式方程求解．

解答：解：

方程两边都乘以最简公分母(x﹣3)(x+1)得：

3(x+1)=5(x﹣3)，

解得：x=9，

检验：当x=9时，(x﹣3)(x+1)=60≠0，

∴原分式方程的解为x=9．

点评：解分式方程的思想是转化即将分式方程转化为整式方程求解；同时要注意解出的x要代入最简公分母中进行检验．

17、(2011•綦江县)计算：|﹣3|﹣(﹣π)⁰++(﹣1)³．

考点：实数的运算；零指数幂；负整数指数幂。

专题：计算题。

分析：根据绝对值、零指数幂、负指数幂、立方四个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．

解答：解：原式=3﹣1+4﹣1=5

点评：本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握负指数幂、零指数幂、立方、绝对值等考点的运算．

16、(2011•綦江县)一个正方体物体沿斜坡向下滑动，其截面如图所示．正方形DEFH的边长为2米，坡角∠A=30°，∠B=90°，BC=6米．当正方形DEFH运动到什么位置，即当AE=米时，有DC²=AE²+BC²．

考点：一元二次方程的应用；含30度角的直角三角形；勾股定理。

分析：根据已知得出假设AE=x，可得EC=12﹣x，利用勾股定理得出DC²=DE²+EC²=4+(12﹣x)²，AE²+BC²=x²+36，即可求出x的值．

解答：解：假设AE=x，可得EC=12﹣x，

∵坡角∠A=30°，∠B=90°，BC=6米，

∴AC=12米，

∵正方形DEFH的边长为2米，即DE=2米，

∴DC²=DE²+EC²=4+(12﹣x)²，

AE²+BC²=x²+36，

∵DC²=AE²+BC²，

∴4+(12﹣x)²=x²+36，

解得：x=米．

故答案为：．

点评：此题主要考查了勾股定理的应用以及一元二次方程的应用，根据已知表示出CE，AE的长度是解决问题的关键．

15、(2011•綦江县)在不透明的口袋中，有四个形状、大小、质地完全相同的小球，四个小球上分别标有数字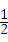，2，4，﹣，现从口袋中任取一个小球，并将该小球上的数字作为平面直角坐标系中点P的横坐标，且点P在反比例函数y=图象上，则点P落在正比例函数y=x图象上方的概率是．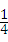

考点：概率公式；正比例函数的图象；反比例函数图象上点的坐标特征。

分析：首先由点P在反比例函数y=图象上，即可求得点P的坐标，然后找到点P落在正比例函数y=x图象上方的有几个，根据概率公式求解即可．

解答：解：∵点P在反比例函数y=图象上，

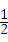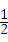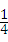∴点P的坐标可能为：(，2)，(2，)，(4，)，(﹣，﹣3)，

∵点P落在正比例函数y=x图象上方的有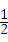：(，2)，

∴点P落在正比例函数y=x图象上方的概率是．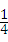

故答案为：．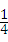

点评：此题考查了反比例函数与一次函数与点的关系，以及概率公式的应用．注意概率=所求情况数与总情况数之比．