23、(2011•江津区)A、B两所学校在一条东西走向公路的同旁，以公路所在直线为x轴建立如图所示的平面直角坐标系，且点A的坐标是(2，2)，点B的坐标是(7，3)．

(1)一辆汽车由西向东行驶，在行驶过程中是否存在一点C，使C点到A、B两校的距离相等，如果有？请用尺规作图找出该点，保留作图痕迹，不求该点坐标．

(2)若在公路边建一游乐场P，使游乐场到两校距离之和最小，通过作图在图中找出建游乐场P的位置，并求出它的坐标．

考点：一次函数综合题；线段垂直平分线的性质；作图-应用与设计作图；轴对称-最短路线问题。

专题：综合题。

分析：(1)连接AB，作出线段AB的垂直平分线，与x轴的交点即为所求的点；

(2)找到点A关于x轴的对称点，连接对称点与点B与x轴交点即为所求作的点．

解答：解：(1)存在满足条件的点C；

作出图形，如图所示．

(2)作点A关于x轴对称的点A′(2，﹣2)，连接A′B，与x轴的交点即为所求的点P．设A′B所在直线的解析式为：y=kx+b，

把(2，2)和(7，3)代入得：，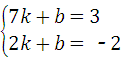

解得：，

∴y=x﹣4，

当y=0时，x=4，

所以交点P为(4，0)．

点评：本题是一道典型的一次函数综合题，题目中还涉及到了线段的垂直平分线的性质及轴对称的问题．

22、(2011•江津区)在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．

(1)求证：Rt△ABE≌Rt△CBF；

(2)若∠CAE=30°，求∠ACF的度数．

考点：全等三角形的判定与性质。

专题：几何图形问题；证明题；数形结合。

分析：(1)由AB=CB，∠ABC=90°，AE=CF，即可利用HL证得Rt△ABE≌Rt△CBF；

(2)由AB=CB，∠ABC=90°，即可求得∠CAB与∠ACB的度数，即可得∠BAE的度数，又由Rt△ABE≌Rt△CBF，即可求得∠BCF的度数，则由∠ACF=∠BCF+∠ACB即可求得答案．

解答：解：(1)证明：∵∠ABC=90°，

∴∠CBF=∠ABE=90°，

在Rt△ABE和Rt△CBF中，，

∴Rt△ABE≌△Rt△CBF(HL)；

(2)∵AB=BC，∠ABC=90°，

∴∠CAB=∠ACB=45°，

又∵∠BAE=∠CAB﹣∠CAE=45°﹣30°=15°，

由(1)知：Rt△ABE≌Rt△CBF，

∴∠BCF=∠BAE=15°，

∴∠ACF=∠BCF+∠ACB=45°+15°=60°．

点评：此题考查了直角三角形全等的判定与性质．此题难度不大，解题的关键是注意数形结合思想的应用．

21、(2011•江津区)计箅：

(1)

(2)解不等式组：，并把解集在数轴上表示出来．

(3)先化简，再求值：，其中．

考点：分式的化简求值；零指数幂；负整数指数幂；在数轴上表示不等式的解集；解一元一次不等式组；特殊角的三角函数值。

分析：(1)分别根据负整数指数幂、0指数幂、绝对值及特殊角的三角函数值计算出各数，再根据实数混合运算的法则进行计算即可；

(2)分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可；

(3)先根据分式混合运算的法则把原式化为最简形式，再把x=代入进行计算即可．

解答：解：(1)原式=3﹣2+2×+1，

=3；

(2)，

由①得，x＞﹣2，

由②得，x＜4，

故原不等式组的解集为：﹣2＜x＜4，

在数轴上表示为：

(3)原式=÷，

=×，

=；

当x=时，原式=1﹣=．．

点评：本题考查的是负整数幂、0指数幂及特殊角的三角函数值，解一元一次不等式组，熟知运算的性质是解答此题的关键．

20、(2011•江津区)如图，在平面直角坐标系中有一矩形ABCD，其中A(0，0)，B (8，0)，D (0，4)，若将△ABC沿AC所在直线翻折，点B落在点E处．则E点的坐标是．

考点：翻折变换(折叠问题)；坐标与图形性质。

专题：探究型。

分析：设E(x，y)，连BE，与OB交于E，作EF⊥AB，由面积法可求得BG的长，在Rt△AEF和Rt△EFB中，由勾股定理知：AF=AE2﹣EF2=BE2﹣BF2，解得x的值，再求得y的值即可

解答：解：连接BE，与AC交于G，作EF⊥AB，

∵AB=AE，∠BAC=∠EAC，

∴△AEB是等腰三角形，AG是BE边上的高，

∴EG=GB，EB=2EG，

BG===，

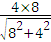设D(x，y)，则有：OD2﹣OF2=AD2﹣AF2，AE2﹣AF2=BE2﹣BF2即：

82﹣x2=(2BG)2﹣(8﹣x)2，

解得：x=，

y=EF=，

∴E点的坐标为：(，)．

故答案为：(，)．

点评：本题考查的是图形的翻折变换，涉及到勾股定理，等腰三角形的判定与性质，根据题意作出辅助线，构造出等腰三角形是解答此题的关键．

19、(2011•江津区)如图，点A、B、C在直径为2的⊙O上，∠BAC=45°，则图中阴影部分的面积等于．(结果中保留π)．

考点：扇形面积的计算；圆周角定理。

专题：几何图形问题；数形结合。

分析：首先连接OB，OC，即可求得∠BOC=90°，然后求得扇形OBC的面积与△OBC的面积，求其差即是图中阴影部分的面积．

解答：解：连接OB，OC，

∵∠BAC=45°，

∴∠BOC=90°，

∵⊙O的直径为2，

∴OB=OC=，

∴S扇形OBC==π，S△OBC=××=，

∴S阴影=S扇形OBC﹣S△OBC=π﹣．

故答案为：π﹣．

点评：此题考查了圆周角的性质，扇形的面积与直角三角形面积得求解方法．此题难度不大，解题的关键是注意数形结合思想的应用．

18、(2011•江津区)将抛物线：y=x2﹣2x向上平移3个单位，再向右平移4个单位得到的抛物线是　y=(x﹣5)2+2或y=x2﹣10x+27　．

考点：二次函数图象与几何变换。

专题：几何变换。

分析：先将抛物线的解析式化为顶点式，然后根据平移规律平移即可得到解析式．

解答：解：y=x2﹣2x=(x﹣1)2﹣1，

根据平移规律，向上平移3个单位，再向右平移4个单位得到的抛物线是：

y=(x﹣5)2+2，

将顶点式展开得，y=x2﹣10x+27．

故答案为：y=(x﹣5)2+2或y=x2﹣10x+27．

点评：主要考查的是函数图象的平移，用平移规律“左加右减，上加下减”直接代入函数解析式求得平移后的函数解析式．

17、(2011•江津区)在一个袋子里装有10个球，其中6个红球，3个黄球，1个绿球，这些球除颜色外，形状、大小、质地等完全相同，充分搅匀后，在看不到球的条件下，随机从这个袋子中摸出一球，不是红球的概率是．

考点：概率公式。

分析：根据随机事件概率大小的求法，找准两点：①符合条件的情况数目；②全部情况的总数．二者的比值就是其发生的概率的大小．

解答：解：红球的概率：(3+1)÷10=．

故答案为：．

点评：此题主要考查了概率的求法与运用，一般方法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P(A)=．

16、(2011•江津区)已知如图，在圆内接四边形ABCD中，∠B=30°，则∠D=　150°　．

考点：圆内接四边形的性质。

分析：根据圆内接四边形对角互补，直接求出即可．

解答：解：∵圆内接四边形ABCD中，∠B=30°，

∴∠D=180°﹣30°=150°．

故答案为：150°．

点评：此题主要考查了圆内接四边形的性质，灵活应用圆内接四边形的性质是解决问题的关键．

15、(2011•江津区)在Rt△ABC中，∠C=90°，BC=5，AB=12，sinA=．

考点：锐角三角函数的定义。

专题：计算题。

分析：在Rt△ABC中，根据三角函数定义sinA=即可求出．

解答：解：∵在Rt△ABC中，∠C=90°，BC=5，AB=12，

∴根据三角函数的定义得：sinA==，

故答案为．

点评：此题比较简单，考查的是锐角三角函数的定义，解答此类题目的关键是画出图形便可直观解答．

14、(2011•江津区)函数中x的取值范围是　x＞2　．

考点：函数自变量的取值范围。

专题：计算题。

分析：由于是二次根式，同时也在分母的位置，由此即可确定x的取值范围．

解答：解：∵是二次根式，同时也是分母，

∴x﹣2＞0，

∴x＞2．

故答案为：x＞2．

点评：本题主要考查的知识点为：分式有意义，分母不为0；二次根式的被开方数是非负数．