7、(2011•重庆)已知抛物线y=ax²+bx+c(a≠0)在平面直角坐标系中的位置如图所示，则下列结论中，正确的是(　)

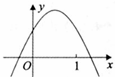
　　 A、a＞0　　 B、b＜0

　　 C、c＜0　　 D、a+b+c＞0

考点：二次函数图象与系数的关系。

专题：数形结合。

分析：根据抛物线的开口方向判断a的正负；根据对称轴在y轴的右侧，得到a，b异号，可判断b的正负；根据抛物线与y轴的交点为(0，c)，判断c的正负；由自变量x=1得到对应的函数值为正，判断a+b+c的正负．

解答：解：∵抛物线的开口向下，

∴a＜0；

又∵抛物线的对称轴在y轴的右侧，

∴a，b异号，

∴b＞0；

又∵抛物线与y轴的交点在x轴上方，

∴c＞0，

又x=1，对应的函数值在x轴上方，

即x=1，y=ax²+bx+c=a+b+c＞0；

所以A，B，C选项都错，D选项正确．

故选D．

点评：本题考查了抛物线y=ax²+bx+c(a≠0)中各系数的作用：a＞0，开口向上，a＜0，开口向下；对称轴为x=﹣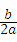，a，b同号，对称轴在y轴的左侧；a，b异号，对称轴在y轴的右侧；抛物线与y轴的交点为(0，c)，c＞0，与y轴正半轴相交；c＜0，与y轴负半轴相交；c=0，过原点．

6、(2011•重庆)如图，⊙O是△ABC的外接圆，∠OCB=40°，则∠A的度数等于(　)

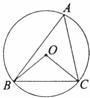
　　 A、60°　　 B、50°

　　 C、40°　　 D、30°

考点：圆周角定理。

分析：在等腰三角形OCB中，求得两个底角∠OBC、∠0CB的度数，然后根据三角形的内角和求得∠COB=100°；最后由圆周角定理求得∠A的度数并作出选择．

解答：解：在△OCB中，OB=OC(⊙O的半径)，

∴∠OBC=∠0CB(等边对等角)；

∵∠OCB=40°，∠C0B=180°﹣∠OBC﹣∠0CB，

∴∠COB=100°；

又∵∠A=∠C0B(同弧所对的圆周角是所对的圆心角的一半)，

∴∠A=50°，

故选B．

点评：本题考查了圆周角定理：同弧所对的圆周角是所对的圆心角的一半．解题时，借用了等腰三角形的两个底角相等和三角形的内角和定理．

5、(2011•重庆)下列调查中，适宜采用抽样方式的是(　)

　　 A、调查我市中学生每天体育锻炼的时间　　 B、调查某班学生对“五个重庆”的知晓率

　　 C、调查一架“歼20”隐形战机各零部件的质量　　　 D、调查广州亚运会100米参赛运动员兴奋剂的使用情况

考点：全面调查与抽样调查。

专题：应用题。

分析：调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来，具体问题具体分析．普查结果准确，所以在要求精确、难度相对不大，实验无破坏性的情况下应选择普查方式；当考查的对象很多或考查会给被调查对象带来损伤破坏，以及考查经费和时间都非常有限时，普查就受到限制，这时就应选择抽样调查．

解答：解：A、调查我市中学生每天体育锻炼的时间，适合抽样调查，

B、调查某班学生对“五个重庆”的知晓率，采用全面调查，

C、调查一架“歼20”隐形战机各零部件的质量，采用全面调查，

D、调查广州亚运会100米参赛运动员兴奋剂的使用情况，采用全面调查，

故选A．

点评：本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查；对于精确度要求高的调查，事关重大的调查往往选用普查，比较简单．

4、(2011•重庆)如图，AB∥CD，∠C=80°，∠CAD=60°，则∠BAD的度数等于(　)

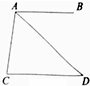
　　 A、60°　　 B、50°

　　 C、45°　　 D、40°

考点：平行线的性质。

分析：根据三角形的内角和为180°，即可求出∠D的度数，再根据两直线平行，内错角相等即可知道∠BAD的度数．

解答：解：∵∠C=80°，∠CAD=60°，

∴∠D=180°﹣80°﹣60°=40°，

∵AB∥CD，

∴∠BAD=∠D=40°．

故选D．

点评：本题考查了三角形的内角和为180°，以及两直线平行，内错角相等的性质，难度适中．

3、(2011•重庆)下列图形中，是中心对称图形的是(　)

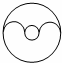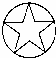　　 A、　　　　 B、　 　 C、　　 D、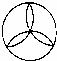

考点：中心对称图形。 　　　　　　　　　 　

专题：数形结合。

分析：根据中心对称图形的定义来判断：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．

解答：解：A、将此图形绕任一点旋转180度都不能与原来的图形重合，所以这个图形不是中心对称图形；

B、将此图形绕某一点旋转180度正好与原来的图形重合，所以这个图形是中心对称图形；

C、将此图形绕任一点旋转180度都不能与原来的图形重合，所以这个图形不是中心对称图形；

D、将此图形绕任一点旋转180度都不能与原来的图形重合，所以这个图形不是中心对称图形．

故选B．

点评：本题主要考查中心对称图形的定义：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．

2、(2011•重庆)计算(a³)²的结果是(　)

　　 A、a　　　　 B、a⁵

　　 C、a⁶　　　 D、a⁹

考点：幂的乘方与积的乘方。

专题：计算题。

分析：根据幂的乘方法则：底数不变，指数相乘．(a^m)ⁿ=a^mn(m，n是正整数)计算即可．

解答：解：(a³)²=a^3×2=a⁶．

故选C．

点评：本题考查了幂的乘方，注意：①幂的乘方的底数指的是幂的底数；②性质中“指数相乘”指的是幂的指数与乘方的指数相乘，这里注意与同底数幂的乘法中“指数相加”的区别．

1、(2011•重庆)在﹣6，0，3，8这四个数中，最小的数是(　)

　　 A、﹣6　　　 B、0

　　 C、3　　　　 D、8

考点：有理数大小比较。

专题：计算题。

分析：根据正数大于0，0大于负数，正数大于负数，两负数绝对值大的反而小，解答即可．

解答：解：∵8＞3＞0＞﹣6，

∴最小的数是﹣6．

故选A．

点评：本题考查了有理数大小的比较，熟记：正数大于0，0大于负数，正数大于负数，两负数绝对值大的反而小．

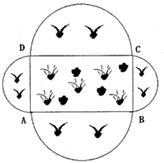
26、(2011•江津区)在“五个重庆”建设中，为了提高市民的宜居环境，某区规划修建一个文化广场(平面图形如图所示)，其中四边形ABCD是矩形，分别以AB、BC、CD、DA边为直径向外作半圆，若整个广场的周长为628米，设矩形的边长AB=y米，BC=x米．(注：取 π=3.14)

(1)试用含x的代数式表示y；

(2)现计划在矩形ABCD区域上种植花草和铺设鹅卵石等，平均每平方米造价为428 元，在四个半圆的区域上种植草坪及铺设花岗岩，平均每平方米造价为400元；

①设该工程的总造价为W元，求W关于x的函数关系式；

②若该工程政府投入1千万元，问能否完成该工程的建设任务？若能，请列出设计方案，若不能，请说明理由？

③若该工程在政府投入1千万元的基础上，又增加企业募捐资金64.82万元，但要求矩形的边BC的长不超过AB长的三分之二，且建设广场恰好用完所有资金，问：能否完成该工程的建设任务？若能，请列出所有可能的设计方案，若不能，请说明理由．

考点：二次函数的应用。

专题：工程问题。

分析：(1)把组合图形惊醒分割拼凑，利用圆的周长计算公式解答整理即可；

(2)①利用组合图形的特点，算出种植花草和铺设鹅卵石各自的面积，进一步求得该工程的总造价即可解答；

②利用配方法求得最小值进行验证即可得出结论；

③建立不等式与一元二次方程，求出答案结合实际即可解决问题．

解答：解：(1)由题意得，

πy+πx=628，

∵3.14y+3.14x=628，

∴y+x=200则y=200﹣x；

(2)①W=428xy+40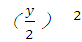0π+400π，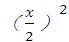

=428x(200﹣x)+400×3.14×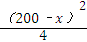+400×3.14×，

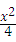=200x2﹣40000x+12560000；

②仅靠政府投入的1千万不能完成该工程的建设任务．理由如下，

由①知W=200(x﹣100)2+1.056×107＞107，

所以不能；

③由题意可知：x≤y即x≤(200﹣x)解之得x≤80，

∴0≤x≤80，

又题意得：W=200(x﹣100)2+1.056×107=107+6.482×105，

整理得(x﹣100)2=441，

解得x1=79，x2=121(不合题意舍去)，

∴只能取x=79，则y=200﹣79=121；

所以设计方案是：AB长为121米，BC长为79米，再分别以各边为直径向外作半圆．

点评：此题利用基本数量关系和组合图形的面积列出二次函数，运用配方法求得最值，进一步结合不等式与一元二次方程解决实际问题．

25、(2011•江津区)已知双曲线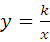：与抛物线：y=ax2+bx+c交于A(2，3)、B(m，2)、C(﹣3，n)三点．

(1)求双曲线与抛物线的解析式；

(2)在平面直角坐标系中描出点A、点B、点C，并求出△ABC的面积．

考点：二次函数综合题。

专题：代数几何综合题。

分析：(1)函数图象过某一点时，这点就满足关系式，利用待定系数法分别求出反比例函数与二次函数解析式即可；

(2)根据A，B，C三点的坐标可以得出△ADB，△BCE和梯形ADEC的面积，用梯形面积减去两三角形面积即可得到△ABC的面积．

解答：解：(1)把点A(2，3)代入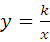得：k=6，

∴y=，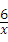

把B(m，2)、(﹣3，n)分别代入y=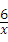得，

m=3，n=﹣2，

把A(2，3)、B(3，2)、C(﹣3，﹣2)分别代入y=ax2+bx+c得：

，

解得：，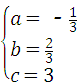

∴抛物线的解析式为：y=﹣x2+x+3；

(2)描点画图得：

S△ABC=S梯形ADEC﹣S△ADB﹣S△BCE，

=(1+6)×5﹣×1×1﹣×6×4，

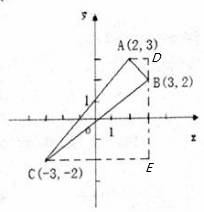
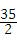=﹣﹣12，

=5．

点评：此题主要考查了二次函数的综合应用以及待定系数法求函数解析式，二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握．

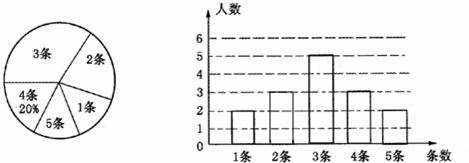
24、(2011•江津区)在“传箴言”活动中，某党支部对全体党员在一个月内所发箴言条数情况进行了统计，并制成了如下两幅不完整的统计图．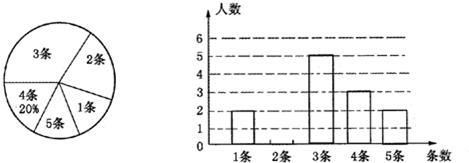

(1)求该支部党员一个月内所发箴言的平均条数是多少？并将该条形统计图补充完整；

(2)如果发了三条箴言的党员中有两位男党员，发了四条箴言的党员有两位女党员，在 发了三条箴言和四条箴言的党员中分别选出一位参加区委组织的“传箴言”活动总结会，请你用列表或树状图的方法，求出所选两位党员恰好是一男一女的概率．

考点：条形统计图；扇形统计图；列表法与树状图法。

专题：图表型。

分析：(1)用箴言3条的人数除以其所占百分比即可得到总人数，然后用总人数减去其他的即可得到发两条的人数，补全图象即可；

(2)将所有可能通过列表或树状图一一列举出来，找到恰好是一男一女的情况计算出概率即可．

解答：解：(1)3÷20%=15条，

∴发两条的有15﹣2﹣5﹣3﹣2=2条，

平均条数=(1×2+2×3+3×5+4×3+5×2)÷15=3条

(2)树状图：

点评：本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．