
题目列表(包括答案和解析)
17、(2011•重庆)|﹣3|+(﹣1)2011×(π﹣3)0﹣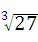 +
+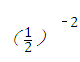 .
.
考点:实数的运算;零指数幂;负整数指数幂。
专题:计算题。
分析:先算出﹣3的绝对值是3,﹣1的奇数次方仍然是﹣1,任何数(0除外)的0次方都等于1,然后按照常规运算计算本题.
解答:解:原式=3+(﹣1)×1﹣3+4
=3
点评:本题考查了绝对值、零指数幂、负整数指数幂、立方根的运算.
16、(2011•重庆)某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,则黄花一共用了 4380 朵.
考点:三元一次方程组的应用。
专题:应用题。
分析:题中有两个等量关系:甲种盆景所用红花的朵数+乙种盆景所用红花的朵数+丙种盆景所用红花的朵数=2900朵,甲种盆景所用紫花的朵数+丙种盆景所用紫花的朵数=3750朵.据此可列出方程组,设步行街摆放有甲、乙、丙三种造型的盆景分别有x盆、y盆、z盆,用含x的代数式分别表示y、z,即可求出黄花一共用的朵数.
解答:解:设步行街摆放有甲、乙、丙三种造型的盆景分别有x盆、y盆、z盆.
由题意,有 ,
,
由①得,3x+2y+2z=580③,
由②得,x+z=150④,
把④代入③,得x+2y=280,
∴2y=280﹣x⑤,
由④得z=150﹣x⑥.
∴4x+2y+3z=4x+(280﹣x)+3(150﹣x)=730,
∴黄花一共用了:24x+12y+18z=6(4x+2y+3z)=6×730=4380.
故黄花一共用了4380朵.
点评:本题考查了三元一次方程组在实际生活中的应用.解题的关键是发掘等量关系列出方程组,难点是将方程组中的其中一个未知数看作常数,用含有一个未知数的代数式表示另外两个未知数,然后代入所求黄花的代数式.
15、(2011•重庆)有四张正面分别标有数学﹣3,0,1,5的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数学记为a,则使关于x的分式方程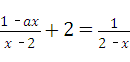 有正整数解的概率为
有正整数解的概率为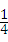 .
.
考点:概率公式;解分式方程。
专题:计算题。
分析:易得分式方程的解,看所给4个数中,能使分式方程有整数解的情况数占总情况数的多少即可.
解答:解:解分式方程得:x=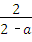 ,
,
能使该分式方程有正整数解的只有0(a=1时得到的方程的根为增根),
∴使关于x的分式方程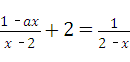 有正整数解的概率为
有正整数解的概率为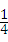 .
.
故答案为: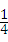 .
.
点评:考查概率的求法;用到的知识点为:概率=所求情况数与总情况数之比.得到使分式方程有整数解的情况数是解决本题的关键.
14、(2011•重庆)在半径为 的圆中,45°的圆心角所对的弧长等于 1 .
的圆中,45°的圆心角所对的弧长等于 1 .
考点:弧长的计算。
专题:计算题。
分析:根据弧长公式l=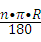 把半径和圆心角代入进行计算即可.
把半径和圆心角代入进行计算即可.
解答:解:45°的圆心角所对的弧长= =1.
=1.
故答案为1.
点评:本题考查了弧长公式:l=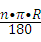 (n为圆心角的度数,R为半径).
(n为圆心角的度数,R为半径).
13、(2011•重庆)在参加“森林重庆”的植树活动中,某班六个绿化小组植树的棵数分别是:10,9,9,10,11,9.则这组数据的众数是 9 .
考点:众数。
专题:计算题。
分析:众数是一组数据中出现次数最多的数据,有时众数可以不止一个.
解答:解:在这一组数据中9是出现次数最多的,故众数是9;
故答案为9.
点评:本题为统计题,考查众数定义.如果众数的概念掌握得不好,就会出错.
12、(2011•重庆)如图,△ABC中,DE∥BC,DE分别交边AB、AB于D、E两点,若AD:AB=1:3,则△ADE与△ABC的面积比为 1:9 .
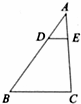
考点:相似三角形的判定与性质。
分析:根据相似三角形的面积比等于相似比的平方直接得出答案.
解答:解:∵△ABC中,DE∥BC,
∴△ADE∽△ABC,
相似比为AD:AB=1:3,
∴△ADE与△ABC的面积比为:1:9.
故答案为:1:9.
点评:此题主要考查了相似三角形的性质,根据相似比性质得出面积比是解决问题的关键.
11、(2011•重庆)据第六次全国人口普查结果显示,重庆常住人口约为2880万人.将数2880万用科学记数法表示为 2.88×103万.
考点:科学记数法-表示较大的数。
专题:数字问题。
分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解答:解:将2880万用科学记数法表示为2.88×103.
故答案是:2.88×103.
点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
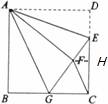
10、(2011•重庆)如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
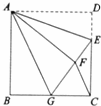
A、1 B、2
C、3 D、4
考点:翻折变换(折叠问题);全等三角形的判定与性质;勾股定理。
专题:几何综合题。
分析:根据翻折变换的性质和正方形的性质可证△ABG≌△AFG;在直角△ECG中,根据勾股定理可证BG=GC;通过证明∠AGB=∠AGF=∠GFC=∠GCF,由平行线的判定可得AG∥CF;由于S△FGC=S△GCE﹣S△FEC,求得面积比较即可.
解答:解:①正确.因为AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴△ABG≌△AFG;
②正确.因为:EF=DE= CD=2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.所以BG=3=6﹣3=GC;
CD=2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.所以BG=3=6﹣3=GC;
③正确.因为CG=BG=GF,所以△FGC是等腰三角形,∠GFC=∠GCF.又∠AGB=∠AGF,∠AGB+∠AGF=180°﹣∠FGC=∠GFC+∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF;
④错误.
过F作FH⊥DC,
∵BC⊥DH,
∴FH∥GC,
∴△EFH∽△EGC,
∴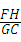 =
=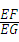 ,
,
EF=DE=2,GF=3,
∴EG=5,
∴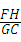 =
=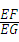 =
=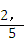 ,
,
∴S△FGC=S△GCE﹣S△FEC= ×3×4﹣
×3×4﹣ ×4×(
×4×(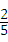 ×3)=
×3)=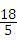 ≠3.
≠3.
故选C.
点评:本题综合性较强,考查了翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算,有一定的难度.
9、(2011•重庆)下列图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形中一共有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,…则第⑥个图形中平行四边形的个数为( )
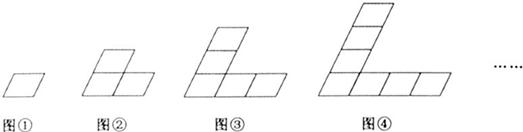
A、55 B、42
C、41 D、29
考点:规律型:图形的变化类。
专题:规律型。
分析:由于图②5个=1+2+2,图③11个=1+2+3+2+3,图④19=1+2+3+4+2+3+4,由此即可得到第⑥个图形中平行四边形的个数.
解答:解:∵图②平行四边形有5个=1+2+2,
图③平行四边形有11个=1+2+3+2+3,
图④平行四边形有19=1+2+3+4+2+3+4,
∴图⑥的平行四边形的个数为1+2+3+4+5+6+2+3+4+5+6=41.
故选C.
点评:本题是一道根据图形进行数字猜想的问题,关键是通过归纳与总结,得到其中的规律,然后利用规律解决一般问题.
8、(2011•重庆)为了建设社会主义新农村,我市积极推进“行政村通畅工程”.张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间的道路改造.下面能反映该工程尚未改造的道路里程y(公里)与时间x(天)的函数关系的大致图象是( )
A、 B、
B、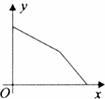
C、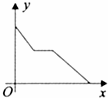 D、
D、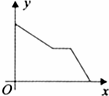
考点:函数的图象。
专题:数形结合。
分析:根据y随x的增大而减小,即可判断选项A错误;根据施工队在工作了一段时间后,因暴雨被迫停工几天,即可判断选项B错误;根据施工队随后加快了施工进度得出y随x的增大减小得比开始的快,即可判断选项C、D的正误.
解答:解:∵y随x的增大而减小,
∴选项A错误;
∵施工队在工作了一段时间后,因暴雨被迫停工几天,
∴选项B错误;
∵施工队随后加快了施工进度,
∴y随x的增大减小得比开始的快,
∴选项C错误;选项D正确;
故选D.
点评:本题主要考查对函数图象的理解和掌握,能根据实际问题所反映的内容来观察与理解图象是解答此题的关键.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com