1．-2的相反数是(　 )

A、 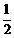　　　　　 B、 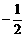　　 　　　　 C、-2　　　　　 D、2

26、(2011•重庆)如图，矩形ABCD中，AB=6，BC=2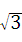，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点发发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t秒(t≥0)．

(1)当等边△EFG的边FG恰好经过点C时，求运动时间t的值；

(2)在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请直接写出S与t之间的函数关系式和相应的自变量t的取值范围；

(3)设EG与矩形ABCD的对角线AC的交点为H，是否存在这样的t，使△AOH是等腰三角形？若存大，求出对应的t的值；若不存在，请说明理由．

考点：相似三角形的判定与性质；根据实际问题列二次函数关系式；等腰三角形的性质；等边三角形的性质；矩形的性质；解直角三角形。

专题：代数几何综合题；动点型；分类讨论。

分析：(1)当边FG恰好经过点C时，∠CFB=60°，BF=3﹣t，在Rt△CBF中，解直角三角形可求t的值；

(2)按照等边△EFG和矩形ABCD重叠部分的图形特点，分为0≤t＜1，1≤t＜3，3≤t＜4，4≤t＜6四种情况，分别写出函数关系式；

(3)存在．当△AOH是等腰三角形时，分为AH=AO=3，HA=HO，OH=OA三种情况，分别画出图形，根据特殊三角形的性质，列方程求t的值．

解答：解：(1)当边FG恰好经过点C时，∠CFB=60°，BF=3﹣t，在Rt△CBF中，BC=2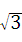，tan∠CFB=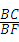，即tan60=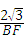，解得BF=2，即3﹣t=2，t=1，∴当边FG恰好经过点C时，t=1；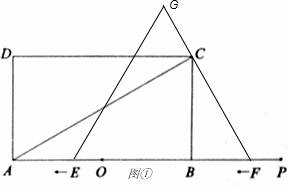

(2)当0≤t＜1时，S=2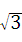t+4；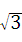

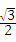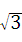当1≤t＜3时，S=﹣t²+3t+；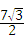

当3≤t＜4时，S=﹣4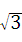t+20；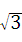

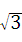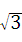当4≤t＜6时，S=t²﹣12t+36；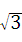

(3)存在．

理由如下：在Rt△ABC中，tan∠CAB==，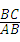

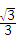∴∠CAB=30°，又∵∠HEO=60°，∴∠HAE=∠AHE=30°，

∴AE=HE=3﹣t或t﹣3，

1)当AH=AO=3时，(如图②)，过点E作EM⊥AH于M，则AM=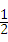AH=，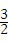

在Rt△AME中，cos∠MAE═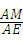，即cos30°=，

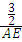∴AE=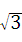，即3﹣t=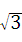或t﹣3=，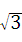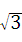

∴t=3﹣或t=3+，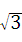

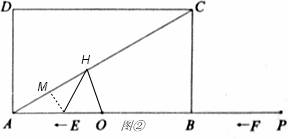
2)当HA=HO时，(如图③)则∠HOA=∠HAO=30°，

又∵∠HEO=60°，∴∠EHO=90°，EO=2HE=2AE，

又∵AE+EO=3，∴AE+2AE=3，AE=1，

即3﹣t=1或t﹣3=1，∴t=2或t=4；

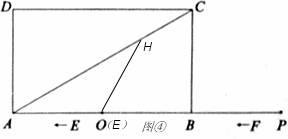
3)当OH=OA时，(如图④)，则∠OHA=∠OAH=30°，

∴∠HOB=60°=∠HEB，∴点E和点O重合，

∴AE=3，即3﹣t=3或t﹣3=3，t=6(舍去)或t=0；

综上所述，存在5个这样的t值，使△AOH是等腰三角形，即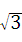t=3﹣或t=3+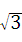或t=2或t=2或t=0．

点评：本题考查了特殊三角形、矩形的性质，相似三角形的判定与性质，解直角三角形的有关知识．关键是根据特殊三角形的性质，分类讨论．

25、(2011•重庆)某企业为重庆计算机产业基地提供电脑配件，受美元走低的影响，从去年1至9月，该配件的原材料价格一路攀升，每件配件的原材料价格y₁(元)与月份x(1≤x≤9，且x取整数)之间的函数关系如下表：

随着国家调控措施的出台，原材料价格的涨势趋缓，10至12月每件配件的原材料价格y₂(元)与月份x(10≤x≤12，且x取整数)之间存在如图所示的变化趋势：

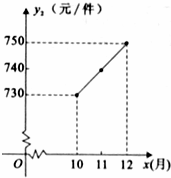(1)请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y₁与x之间的函数关系式，根据如图所示的变化趋势，直接写出y₂与x之间满足的一次函数关系式；

(2)若去年该配件每件的售价为1000元，生产每件配件的人力成本为50元，其它成本30元，该配件在1至9月的销售量p₁(万件)与月份x满足函数关系式p₁=0.1x+1.1(1≤x≤9，且x取整数)10至12月的销售量p₂(万件)与月份x满足函数关系式p₂=﹣0.1x+2.9(10≤x≤12，且x取整数)．求去年哪个月销售该配件的利润最大，并求出这个最大利润；

(3)今年1至5月，每件配件的原材料价格均比去年12月上涨60元，人力成本比去年增加20%，其它成本没有变化，该企业将每件配件的售价在去年的基础上提高a%，与此同时每月销售量均在去年12月的基础上减少0.1a%．这样，在保证每月上万件配件销量的前提下，完成了1至5月的总利润1700万元的任务，请你参考以下数据，估算出a的整数值．

(参考数据：99²=9901，98²=9604，97²=9409，96²=9216，95²=9025)

考点：二次函数的应用；一元二次方程的应用；一次函数的应用。

专题：应用题；分类讨论。

分析：(1)把表格(1)中任意2点的坐标代入直线解析式可得y₁的解析式．把(10，730)(12，750)代入直线解析式可得y₂的解析式，；

(2)分情况探讨得：1≤x≤9时，利润=P₁×(售价﹣各种成本)；10≤x≤12时，利润=P₂×(售价﹣各种成本)；并求得相应的最大利润即可；

(3)根据1至5月的总利润1700万元得到关系式求值即可．

解答：解：(1)设y₁=kx+b，

则，

解得，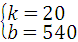

∴y₁=20x+540(1≤x≤9，且x取整数)；

设y₂=ax+b，则，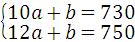

解得，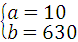

∴y₂=10x+630(10≤x≤12，且x取整数)；

(2)设去年第x月的利润为W元．

1≤x≤9，且x取整数时，W=P₁×(1000﹣50﹣30﹣y₁)=﹣2x²+16x+418=﹣2(x﹣4)²+450，

∴x=4时，W最大=450元；

10≤x≤12，且x取整数时，W=P₂×(1000﹣50﹣30﹣y₂)=(x﹣29)²，

∴x=10时，W最大=361元；

(3)去年12月的销售量为﹣0.1×12+2.9=1.7(万件)，

今年原材料价格为：750+60=810(元)

今年人力成本为：50×(1+20%)=60元．

∴5×[1000×(1+a%)﹣810﹣60﹣30]×1.7(1﹣0.1×a%)=1700，

设t=a%，整理得10t²﹣99t+10=0，

解得t=，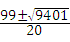

∵9401更接近于9409，

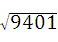∴≈97，

∴t₁≈0.1，t₂≈9.8，

∴a₁≈10或a₂≈980，

∵1.7(1﹣0.1×a%)≥1，

∴a≈10．

答：a的整数解为10．

点评：本题综合考查了一次函数和二次函数的应用；根据二次函数的最值及相应的求值范围得到一定范围内的最大值是解决本题的易错点；利用估算求得相应的整数解是解决本题的难点．

24、(2011•重庆)如图，梯形ABCD中，AD∥BC，∠DCB=45°，CD=2，BD⊥CD．过点C作CE⊥AB于E，交对角线BD于F，点G为BC中点，连接EG、AF．

(1)求EG的长；

(2)求证：CF=AB+AF．

考点：梯形；全等三角形的判定与性质；直角三角形斜边上的中线；勾股定理。

专题：证明题；几何综合题。

分析：(1)根据BD⊥CD，∠DCB=45°，得到∠DBC=∠DCB，求出BD=CD=2，根据勾股定理求出BC=2，根据CE⊥BE，点G为BC的中点即可求出EG；

(2)在线段CF上截取CH=BA，连接DH，根据BD⊥CD，BE⊥CD，推出∠EBF=∠DCF，证出△ABD≌△HCD，得到AD=BD，∠ADB=∠HDC，根据AD∥BC，得到∠ADB=∠DBC=45°，推出∠ADB=∠HDB，证出△ADF≌△HDF，即可得到答案．

解答：(1)解：∵BD⊥CD，∠DCB=45°，

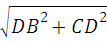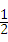∴∠DBC=45°=∠DCB，∴BD=CD=2，在Rt△BDC中BC==2，∵CE⊥BE，点G为BC的中点，∴EG=BC=．

答：EG的长是．

(2)证明：在线段CF上截取CH=BA，连接DH，

∵BD⊥CD，BE⊥CE，

∴∠EBF+∠EFB=90°，∠DFC+∠DCF=90°，

∵∠EFB=∠DFC，

∴∠EBF=∠DCF，

∵DB=CD，BA=CH，

∴△ABD≌△HCD，

∴AD=DH，∠ADB=∠HDC，

∵AD∥BC，

∴∠ADB=∠DBC=45°，

∴∠HDC=45°，∴∠HDB=∠BDC﹣∠HDC=45°，

∴∠ADB=∠HDB，

∵AD=HD，DF=DF，

∴△ADF≌△HDF，

∴AF=HF，

∴CF=CH+HF=AB+AF，

∴CF=AB+AF．

点评：本题主要考查对梯形，全等三角形的性质和判定，平行线的性质，直角三角形斜边上的中线，勾股定理等知识点的理解和掌握，综合运用性质进行推理是解此题的关键．

23、(2011•重庆)为实施“农村留守儿童关爱计划”，某校结全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅不完整的统计图：

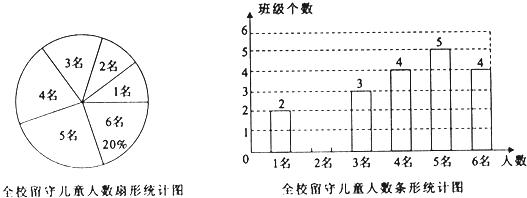
(1)求该校平均每班有多少名留守儿童？并将该条形统计图补充完整；

(2)某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率．

考点：条形统计图；扇形统计图；列表法与树状图法。

专题：计算题；图表型。

分析：(1)根据留守儿童有4名的占20%，可求得留守儿童的总数，再求得留守儿童是2名的班数；

(2)由(1)得只有2名留守儿童的班级有2个，共4名学生．设A₁，A₂来自一个班，B₁，B₂来自一个班，列出树状图可得出来自一个班的共有4种情况，则所选两名留守儿童来自同一个班级的概率．

解答：解：(1)该校班级个数为4÷20%=20(个)，

只有2名留守儿童的班级个数为：20﹣(2+3+4+5+4)=2(个)，

该校平均每班留守儿童的人数为：

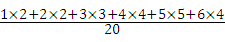=4(名)，

补图如下：

；

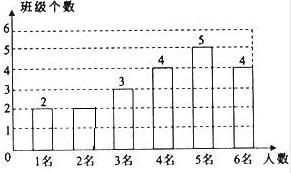(2)由(1)得只有2名留守儿童的班级有2个，共4名学生．设A₁，A₂来自一个班，B₁，B₂来自一个班，

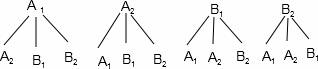
有树状图可知，共有12中等可能的情况，其中来自一个班的共有4种情况，

则所选两名留守儿童来自同一个班级的概率为：=．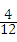

点评：本题是一道统计题，考查了条形统计图和扇形统计图，及树状图的画法，是重点内容，要熟练掌握．

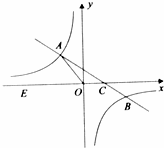
22、(2011•重庆)如图，在平面直角坐标系x0y中，一次函数y=kx+b(k≠0)的图象与反比例函数(m≠0)的图象交于二、四象限内的A、B两点，与x轴交于C点，点B的坐标为(6，n)．线段OA=5，E为x轴上一点，且sin∠AOE=．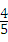

(1)求该反比例函数和一次函数的解析式；

(2)求△AOC的面积．

考点：反比例函数综合题。

专题：综合题。

分析：(1)过点A作AD⊥x轴于D点，由sin∠AOE=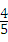，OA=5，根据正弦的定义可求出AD，再根据勾股定理得到DO，即得到A点坐标(﹣3，4)，把A(﹣3，4)代入y=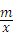，确定反比例函数的解析式为y=﹣；将B(6，n)代入，确定点B点坐标，然后把A点和B点坐标代入y=kx+b(k≠0)，求出k和b．

(2)先令y=0，求出C点坐标，得到OC的长，然后根据三角形的面积公式计算△AOC的面积即可．

解答：解：(1)过点A作AD⊥x轴于D点，如图，

∵sin∠AOE=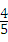，OA=5，

∴sin∠AOE===，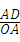

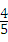∴AD=4，

∴DO==3，

而点A在第二象限，

∴点A的坐标为(﹣3，4)，

将A(﹣3，4)代入y=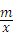，得m=﹣12，

∴反比例函数的解析式为y=﹣；

将B(6，n)代入y=﹣，得n=﹣2；

将A(﹣3，4)和B(6，﹣2)分别代入y=kx+b(k≠0)，得

，

解得，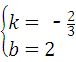

∴所求的一次函数的解析式为y=﹣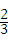x+2；

(2)在y=﹣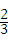x+2中，令y=0，

即﹣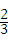x+2=0，

解得x=3，

∴C点坐标为(0，3)，即OC=3，

∴S_△AOC=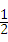•AD•OC=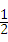•4•3=6．

点评：本题考查了点的坐标的求法和点在图象上，点的横纵坐标满足图象的解析式；也考查了正弦的定义、勾股定理以及三角形面积公式．

21、(2011•重庆)先化简，再求值：，其中x满足x²﹣x﹣1=0．

考点：分式的化简求值。

专题：计算题。

分析：先通分，计算括号里的，再把除法转化成乘法进行约分计算．最后根据化简的结果，可由x²﹣x﹣1=0，求出x+1=x²，再把x²=x+1的值代入计算即可．

解答：解：原式=×=×=，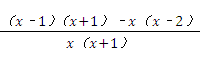

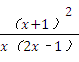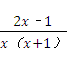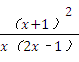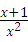∵x²﹣x﹣1=0，

∴x²=x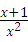+1，

∴==1．

点评：本题考查了分式的化简求值．解题的关键是注意对分式的分子、分母因式分解，除法转化成下乘法．

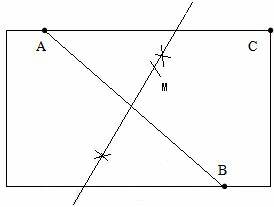
20、(2011•重庆)为进一步打造“宜居重庆”，某区拟在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示．请在答题卷的原图上利用尺规作图作出音乐喷泉M的位置．(要求：不写已知、求作、作法和结论，保留作图痕迹，必须用铅笔作图)

考点：作图-应用与设计作图。

专题：作图题。

分析：易得M在AB的垂直平分线上，且到C的距离等于AB的一半．

解答：解：作AB的垂直平分线，以点C为圆心，以AB的一半为半径画弧交AB的垂直平分线于点M即可．

点评：考查设计作图；得到点M是AB的垂直平分线与以点C为圆心，以AB的一半为半径的弧的交点是解决本题的关键．

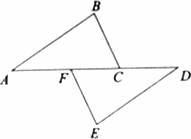
19、(2011•重庆)如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．求证：BC∥EF．

考点：全等三角形的判定与性质；平行线的判定。

专题：证明题。

分析：根据已知条件得出△ACB≌△DEF，即可得出∠ACB=∠DFE，再根据内错角相等两直线平行，即可证明BC∥EF．

解答：证明：∵AF=DC，

∴AC=DF，

又∵AB=DE，∠A=∠D，

∴△ACB≌△DEF，

∴∠ACB=∠DFE，

∴BC∥EF．

点评：本题考查了两直线平行的判定方法，内错角相等，两直线平行，难度适中．

18、(2011•重庆)解不等式2x﹣3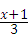＜，并把解集在数轴上表示出来．

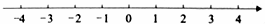
考点：解一元一次不等式；在数轴上表示不等式的解集。

专题：计算题。

分析：先去分母，再去括号、移项、合并同类项，系数化为1，求出不等式的解集，再在数轴上表示出来即可．

解答：解：3(2x﹣3)＜x+1

6x﹣9＜x+1

5x＜10

x＜2

∴原不等式的解集为x＜2，

在数轴上表示为：

点评：本题考查了解简单不等式的能力，解答这类题学生往往在解题时不注意移项要改变符号这一点而出错．