
题目列表(包括答案和解析)
9. 一天有86400秒,用科学记数法表示为____________ 秒;
8. 如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
A.  B.
B.  C.
C.  D.
D.
7. 等腰三角形的两条边长分别为3,6,那么它的周长为( )
A.15 B.12 C.12或15 D.不能确定
6. 如图所示的是某几何体的三视图,则该几何体的形状是( )
A. 长方体 B.三棱柱 C.圆锥 D.正方体
5. 抛物线 可以看作是由抛物线
可以看作是由抛物线 按下列何种变换得到( )
按下列何种变换得到( )
 A. 向上平移5个单位 B. 向下平移5个单位 C. 向左平移5个单位 D. 向右平移5个单位
A. 向上平移5个单位 B. 向下平移5个单位 C. 向左平移5个单位 D. 向右平移5个单位
4. 在平行四边形、等边三角形、菱形、等腰梯形中既是轴对称图形又是中心对称图形的是( )
A. 平行四边形 B. 等边三角形 C.菱形 D.等腰梯形
3. 已知点P( )在平面直角坐标系的第一象限内,则a的取值范围在数轴上可表示为( )
)在平面直角坐标系的第一象限内,则a的取值范围在数轴上可表示为( )
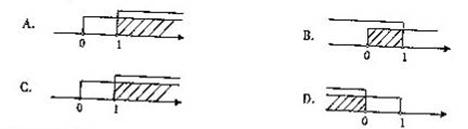
2. 下列运算哪种,正确的是( )
A.  B.
B.  C.
C.  D.
D.
1.  的相反数是( )
的相反数是( )
A.  B.
B. 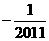 C. 2011 D.
C. 2011 D. 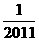
27、(2011•毕节地区)如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
(1)求该抛物线的解析式.
(2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
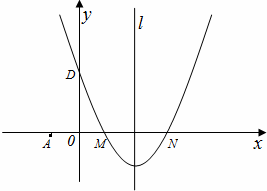
考点:二次函数综合题。
分析:(1)根据图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),可利用交点式求出二次函数解析式;
(2)根据直线AB与抛物线的对称轴和x轴围成的三角形面积为6,得出AC,BC的长,得出B点的坐标,即可利用待定系数法求出一次函数解析式;
(3)利用三角形相似求出△ABC∽△CBM,得出 ,即可求出圆的半径,即可得出P点的坐标.
,即可求出圆的半径,即可得出P点的坐标.
解答:解:(1)∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),
∴假设二次函数解析式为:y=a(x﹣1)(x﹣3),
将D(0,3),代入y=a(x﹣1)(x﹣3),得:
3=3a,
∴a=1,
∴抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3;
(2)∵过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,
∴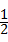 AC×BC=6,
AC×BC=6,
∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,
∴二次函数对称轴为x=2,
∴AC=3,
∴BC=4,
∴B点坐标为:(2,4),
一次函数解析式为;y=kx+b,
∴ ,
,
解得: ,
,
y=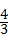 x+
x+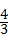 ;
;
(3)∵当点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,
∴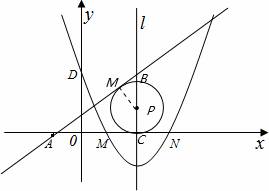 MO⊥AB,AM=AC,PM=PC,
MO⊥AB,AM=AC,PM=PC,
∵AC=1+2=3,BC=4,
∴AB=5,AM=3,
∴BM=2,
∵∠MBP=∠ABC,
∠BMP=∠ACB,
∴△ABC∽△CBM,
∴ ,
,
∴ ,
,
∴PC=1.5,
P点坐标为:(2,1.5).
点评:此题主要考查了二次函数的综合应用,二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com