
题目列表(包括答案和解析)
10.(2011湖北鄂州,10,3分)计算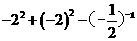 =( )
=( )
A.2 B.-2 C.6 D.10
[解题思路]:正面求解:原式= 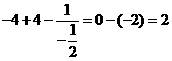
[答案]A
[点评]此题考查有理数的运算包括2的平方的相反数;(-2)的平方;及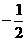 的-1次幂,涉及有理数计算等问题,尤其符号容易出错,需要细心求解。 难度较小
的-1次幂,涉及有理数计算等问题,尤其符号容易出错,需要细心求解。 难度较小
9.(2011湖北鄂州,9,3分)cos30°=( )
A.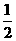 B.
B.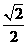 C.
C.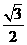 D.
D.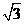
[解题思路]
直接作答:cos30°=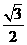 。也可分析A:
。也可分析A: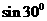 、B:
、B: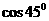 、D:
、D: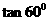
[答案]C
[点评]:直接考查特殊三角函数值,学生可通过记忆特殊三角函数值,也可结合画直角三角形求解。
难度较小。
8.(2011湖北鄂州,8,3分)如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP=_______________.


[解题思路]是利用角平分线的性质定理和判定定理证AP是∠BAC外角的平分线!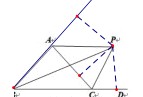 而∠BAC=2∠BPC也是可证的!由∠BPC=40°和角平分线性质,
而∠BAC=2∠BPC也是可证的!由∠BPC=40°和角平分线性质,
得∠ACD-2∠ABC=2×40°=80°即∠BAC=80°,
则∠BAC的外角为100°,∠CAP=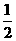 ×100°=50°。
×100°=50°。
[答案]50°
[点评]此题考查学生对角平分线性质和三角形外角的知识,学生要证AP是∠BAC外角的平分线,需要添加辅助线才行。
难度较大
7.(2011湖北鄂州,7,3分)若关于x,y的二元一次方程组 的解满足
的解满足 ,则a的取值范围为______.
,则a的取值范围为______.
[解题思路]:
法一: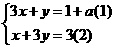 将(1)+(2)得
将(1)+(2)得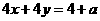 ,则
,则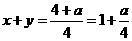 <2 ∴a<4.
<2 ∴a<4.
法二:也可解方程组(用含a的代数式表示x、y,再用含a的代数式表示x+y,解有关a的不等式。
[答案]a<4
[点评]:此题更侧重考查学生的观察能力(1)+(2)系数相同,用法一易得x+y,求解较简便,有整体的数学思想的考查初衷,然后是考查不等式的解法,有一定的综合性。用法二也可,但计算较繁。
难度中等。
6.(2011湖北鄂州,6,3分)如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC、△ADF、△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF=_________.
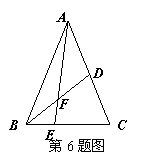

[解题思路]由D是AC的中点且S△ABC=12,可得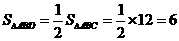 ;同理EC=2BE即EC=
;同理EC=2BE即EC=  ,可得
,可得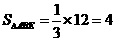 ,又
,又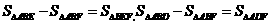 等量代换可知S△ADF-S△BEF=2
等量代换可知S△ADF-S△BEF=2
[答案]2
[点评]此题考查高不变,底为中点或三等分点构成的三角形与原三角形的面积之间的关系,就是底之间的关系;另考查转换的数学思想方法。
难度较小。
5.(2011湖北鄂州,5,3分)如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为_______.
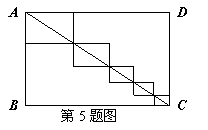

[解题思路]由矩形性质可知∠B=90°,对角线AC=10,BC=8可运用勾股定理得AC=6;再利用平移的知识将每个小矩形的边分别上、下、左、右平移即可发现5个小矩形的周长之和是矩形ABCD的周长=(6+8)×2=28。
[答案]28
[点评]本题考查勾股定理和平移的知识,体现图形变换的数学问题,涉及操作与知识相结合。学生比较容易发现,从而求解。
难度较小
4.(2011湖北鄂州,4,3分)如图:点A在双曲线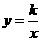 上,AB⊥x轴于B,且△AOB的面积S△AOB=2,则k=______.
上,AB⊥x轴于B,且△AOB的面积S△AOB=2,则k=______.


[解题思路]:由反比例函数解析式可知:系数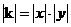 ,
,
∵S△AOB=2即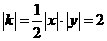 ,∴
,∴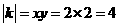 ;
;
又由双曲线在二、四象限k<0,∴k=-4
[答案]-4
[点评]本题考查反比例函数k值的确定,结合三角形面积的2倍即是k的绝对值,再观察反比例函数图像所在的象限,从而确定k的符号。体现数形结合,有一定的综合性。
难度中等
3.(2011湖北鄂州,3,3分)要使式子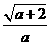 有意义,则a的取值范围为_____________________.
有意义,则a的取值范围为_____________________.
[解题思路]:
此式子要有意义首先分母不为0,分子中的二次根式中的被开方数≥0,所以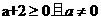 时,才有意义。
时,才有意义。
[答案]a≥-2且a≠0
[点评]本题考查分式有意义分母不为0,二次根式有意义被开方数≥0,同时还涉及解不等式的知识,综合性较强。
难度中等
2.(2011湖北鄂州,2,3分)分解因式8a2-2=____________________________.
[解题思路]本题要先提取公因式2,再运用平方差公式将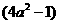 写成
写成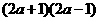 ,即原式可分解为:8a2-2
,即原式可分解为:8a2-2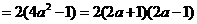
[答案]2(2a+1)(2a-1)
[点评]本题考查了提公因式法,公式法分解因式,先提取公因式后再利用平方差公式继续进行因式分解,分解因式一定要彻底.利用相应的公式和分解因式的先后顺序即可得到答案。(分解因式即将一个多项式写成几个因式的乘积的形式)。
难度中等。
1.(2011湖北鄂州,1,3分)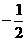 的倒数是________.
的倒数是________.
[解题思路]: 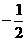 的倒数是:
的倒数是: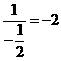 ,。
,。
[答案]-2
[点评]本题考查了倒数的概念,即当a≠0时,a与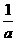 互为倒数。特别要注意的是:负数的倒数还是负数,此题难度较小。
互为倒数。特别要注意的是:负数的倒数还是负数,此题难度较小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com