
题目列表(包括答案和解析)
20.(2011湖北鄂州,20,8分)今年我省干旱灾情严重,甲地急需要抗旱用水15万吨,乙地13万吨.现有A、B两水库各调出14万吨水支援甲、乙两地抗旱.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.
⑴设从A水库调往甲地的水量为x万吨,完成下表


|
甲 |
乙 |
总计 |
||||||
|
A |
x |
|
14 |
||||||
|
B |
|
|
14 |
||||||
|
总计 |
15 |
13 |
28 |
⑵请设计一个调运方案,使水的调运量尽可能小.(调运量=调运水的重量×调运的距离,单位:万吨•千米)
[解题思路]通过读题、审题
(1)完成表格有2个思路:从供或需的角度考虑,均能完成上表。
(2)运用公式(调运水的重量×调运的距离)
总调运量=A的总调运量+B的总调运量调运水的重量×调运的距离
y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275(注:一次函数的最值要得到自变量的取值范围)∵5>0∴y随x的增大而增大,y要最小则x应最大
由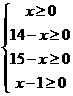 解得1≤x≤14
解得1≤x≤14
y=5x+1275中∵5>0∴y随x的增大而增大,y要最小则x应最小=1
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。
[答案]⑴(从左至右,从上至下)14-x 15-x x-1
⑵y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275
解不等式1≤x≤14
所以x=1时y取得最小值
y=5+1275=1280
∴调运方案为A往甲调1吨,往乙调13吨;B往甲调14吨,不往乙调。
[点评]这样的“方案决策类”试题,其所考查的内容和思想方法却是非常重要的,其考查目的也是一般的函数与不等式题目所不能完全体现的,具有一定的独特性和挑战性.在多数情况下,解这种试题要以“不等式” 作为解决问题的工具,且由于题中含有由“不确定”中找确定的因素,所以关联了函数与不等式等数学模型的建立与应用。此题中要确定一个量的范围的问题,就要转化为不等式的问题.
上题对于学生来说问题情境还是比较熟悉的,且题目中都是显性的条件,学生通过认真审题能比较容易将实际问题转化为数学问题,从而求解。第(2)问需要借助题目中隐含的不等关系--难点,列出不等式组,并确定出不等数组的解,从而利用一次函数的增减性选择最值,得到最佳方案。
难度较大
19.(2011湖北鄂州,19,7分)有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
⑴先后两次抽得的数字分别记为s和t,则︱s-t︱≥1的概率.
⑵甲、乙两人做游戏,现有两种方案.A方案:若两次抽得相同花色则甲胜,否则乙胜.B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.
请问甲选择哪种方案胜率更高?
[解题思路](1)如下表
|
甲(s) 乙(t) |
红桃3 |
红桃4 |
黑桃5 |
|
红桃3 |
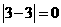 |
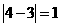 |
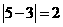 |
|
红桃4 |
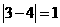 |
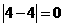 |
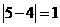 |
|
黑桃5 |
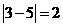 |
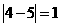 |
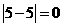 |
由上表可知:︱s-t︱≥1的概率=
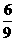 =
= (也可画树形图求解)。
(也可画树形图求解)。
(2)方案A:如表
|
甲(花色) 乙(花色) |
红桃3 |
红桃4 |
黑桃5 |
|
红桃3 |
同色 |
同色 |
不同色 |
|
红桃4 |
同色 |
同色 |
不同色 |
|
黑桃5 |
不同色 |
不同色 |
同色 |
由上表可得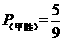
方案B:如表
|
甲 乙 |
红桃3 |
红桃4 |
黑桃5 |
|
红桃3 |
3+3=6 |
3+4=7 |
3+5=8 |
|
红桃4 |
4+3=7 |
4+4=8 |
4+5=9 |
|
黑桃5 |
5+3=8 |
5+4=9 |
5+5=10 |
由上表可得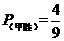
因为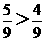 ,所以选择A方案甲的胜率更高.
,所以选择A方案甲的胜率更高.
[答案]⑴ ⑵A方案
⑵A方案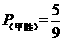 ,B方案
,B方案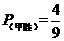 ,故选择A方案甲的胜率更高.
,故选择A方案甲的胜率更高.
[点评]本题考查的是用列表法或画树状图法求概率方法.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
难度中等
18.(2011湖北鄂州,18,7分)如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若AE=4,FC=3,求EF长.


[解题思路]连结BD,证△BED≌△CFD和△AED≌△BFD,得BF=4,BE=3,再运用勾股定理求得EF=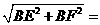 5
5
[答案]连结BD,证△BED≌△CFD和△AED≌△BFD,求得EF=5
[点评]此题考查了直角三角形斜边上的中线是斜边的一半,三角形全等的判定和性质和勾股定理。只要抓住等腰直角三角形的性质和全等三角形的判定,解决起来并不困难。
难度中等
17.(2011湖北鄂州,17,6分)为了加强食品安全管理,有关部门对某大型超市的甲、乙两种品牌食用油共抽取18瓶进行检测,检测结果分成“优秀”、“合格”、“不合格”三个等级,数据处理后制成以下折线统计图和扇形统计图.
⑴甲、乙两种品牌食用油各被抽取了多少瓶用于检测?
⑵在该超市购买一瓶乙品牌食用油,请估计能买到“优秀”等级的概率是多少?


[解题思路](1)分别观察折线和扇形图不合格的1瓶占甲的10%,所以甲被抽取了10瓶,已被抽取了:18-10=8瓶。
(2)结合两图及问题(1)得乙优秀的瓶数共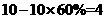 瓶,所以优秀率为
瓶,所以优秀率为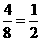
[答案]
⑴(由不合格瓶数为1知道甲不合格的瓶数为1)甲、乙分别被抽取了10瓶、8瓶
⑵P(优秀)=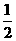
[点评]评析本题以学生在生活中常见的食用油安全问题为素材,以双图(折线统计图+扇形统计图)的形式交叉呈现数据。学生需要通过读图,分析图获得信息,进而深入分析两个图之间相互联系,互相补充获得数据,较好地考查了学生利用统计图描述数据的能力,以及考查学生分析问题和解决问题的能力。在解决问题的过程中只有读懂图才能完成后边的计算问题,问题设计环环相扣,层层递进,这种考法有利于落实对学生的综合判断能力的考查.
难度中等
16.(2011湖北鄂州,16,5分)解方程: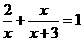
[解题思路]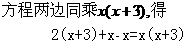
去括号 ,得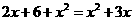
移相合并同类项,得 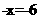
系数化为1,得 x=6
检验:当x=6时,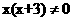 ,所以x=6是原方程的根。
,所以x=6是原方程的根。
[答案]x=6
[点评]考查解最基本的分式方程的技能,学生只要掌握解分式方程的一般步骤即可得分。这种直接考查基本技能的考法有效提高了考查结果的效度和信度.
难度较小
15.(2011湖北鄂州,15,3分)已知函数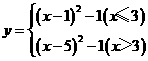 ,则使y=k成立的x值恰好有三个,则k的值为( )
,则使y=k成立的x值恰好有三个,则k的值为( )
A.0 B.1 C.2 D.3
[解题思路]如图: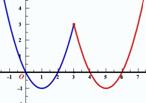
利用顶点式及取值范围,可画出函数图象会发现:当x=3时,y=k成立的x值恰好有三个,此时y=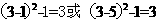 ,则k的值为3。
,则k的值为3。
[答案]D
[点评]用数形结合更容易求解,当y一定时x值得个数也一定,0个、1个、2个、3个、4个几种情况。抓住顶点式和x的取值范围作图是解此题的关键所在。
难度中等
难度中等
14.(2011湖北鄂州,14,3分)如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
A.4 B.8 C.16 D.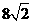
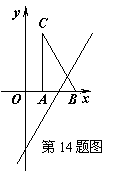

[解题思路]将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时即当y=4时,解得x=5,所以平移的距离为5-1=4,又知BC扫过的图形为平行四边形,高不变为: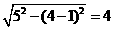 ,所以平行四边形面积=底×高=4×4=16.
,所以平行四边形面积=底×高=4×4=16.
[答案]C
[点评]此题涉及运用勾股定理;已知一次函数解析式中的y值,解函数转化的一元一次方程求出x值,利用横坐标之差计算平移的距离;以及平行四边形面积公式。运用数形结合、平移变换、动静变化的数学思想方法是解此题的关键,综合性较强。
难度中等
13.(2011湖北鄂州,13,3分)如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA=( )
A.30° B.45° C.60° D.67.5°
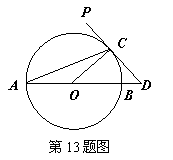

[解题思路]PD切⊙O于点C,交AB的延长线于D,且CO=CD
得∠COD=45°、∠PCO=90°。再由OA=OC,及外角知识得∠ACO=22.5°;
又∠PCA+∠ACO=90°,所以∠PCA=90°-∠ACO=67.5°。
另外也可考虑直径条件连结BC求解。
[答案]D
[点评]本题切线的性质和等边对等角及外角、余角等边角之间的关系。只要充分挖掘条件和图形中边角的内在联系就可顺利求解。
难度较小。
12.(2011湖北鄂州,12,3分)一个几何体的三视图如下:其中主视图都是腰长为4、底边为2的等腰三角形,则这个几何体的侧面展开图的面积为( )
A.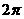 B.
B.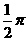 C.
C. 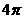 D.
D.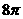


[解题思路]此题宜正面求解。先判断此几何体为圆锥,侧面展开图为扇形;再由三视图得到扇形母线为4、弧长为圆锥底面圆的周长;最后运用公式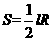 =
= 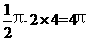
[答案]C
[点评]此题考查学生由三视图判断出几何体为圆锥,再考查圆锥侧面展开图--扇形面积公式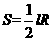 ,需要利用直径求出圆锥底面周长,并将其准确代入对应的公式是解题的关键。
,需要利用直径求出圆锥底面周长,并将其准确代入对应的公式是解题的关键。
难度较小
11.(2011湖北鄂州,11,3分)下列说法中
①一个角的两边分别垂直于另一个角的两边,则这两个角相等
②数据5,2,7,1,2,4的中位数是3,众数是2
③等腰梯形既是中心对称图形,又是轴对称图形
④Rt△ABC中,∠C=90°,两直角边a,b分别是方程x2-7x+7=0的两个根,则AB边上的中线长为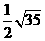
正确命题有( )
A.0个 B.1个 C.2个 D.3个
[解题思路]①:画图可发现应考虑2种情况,还可以互补,命题不正确;②:排列为1,2,2,4,5,7 中位数为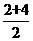 =3,众数为2,命题正确;③等腰梯形只是轴对称图形,不是中心对称图形,命题不正确;
=3,众数为2,命题正确;③等腰梯形只是轴对称图形,不是中心对称图形,命题不正确;
④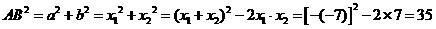 ,
,
∴AB= 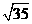 ,而斜边上的中线等于斜边的一半为
,而斜边上的中线等于斜边的一半为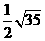 ,正确。
,正确。
所以正确的有②、④,2个。
[答案]C
[点评]本题考查概念有角;中位数、众数;特殊四边形的对称性;一元二次方程根与系数的关系、勾股定理、直角三角形斜边上的中线是斜边的一半等综合了多个基础知识点。认真分析每一个命题,就能正确解答。难度中等
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com