
题目列表(包括答案和解析)
11、(2011•南京)如图,以0为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值等于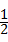 .
.
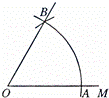
考点:特殊角的三角函数值;等边三角形的判定与性质。
分析:根据作图可以证明△ABC是等边三角形,则∠AOB=60°,据此即可求解.
解答:解:∵OA=OB=AB,
∴△ABC是等边三角形,
∴∠AOB=60°,
∴cos∠AOB=cos60°=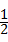 .
.
故答案是: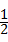 .
.
点评:本题主要考查了特殊角的三角函数值,正确理解△ABC是等边三角形是解题的关键.
10、(2011•南京)等腰梯形的腰长为5cm,它的周长是22cm,则它的中位线长为 6 cm.
考点:梯形中位线定理;等腰梯形的性质。
专题:计算题。
分析:根据等腰梯形的腰长和周长求出AD+BC,根据梯形的中位线定理即可求出答案.
解答:解:∵等腰梯形的腰长为5cm,它的周长是22cm,
∴AD+BC=22﹣5﹣5=12,
∵EF为梯形的中位线,
∴EF=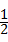 (AD+BC)=6.
(AD+BC)=6.
故答案为:6.
点评:本题主要考查对等腰梯形的性质,梯形的中位线定理等知识点的理解和掌握,理解梯形的中位线定理[知道EF=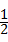 (AD+BC)]是解此题的关键.
(AD+BC)]是解此题的关键.
9、(2011•南京)计算(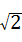 +1)(2﹣
+1)(2﹣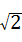 )=
)=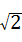 .
.
考点:二次根式的混合运算。
分析:根据二次根式的混合运算直接去括号得出,再进行合并同类项即可.
解答:解:(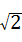 +1)(2﹣
+1)(2﹣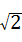 ),
),
=2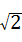 ﹣
﹣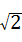 ×
×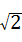 +1×2﹣1×
+1×2﹣1×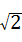 ,
,
=2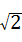 ﹣2+2﹣
﹣2+2﹣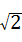 ,
,
=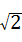 .
.
故答案为: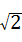 .
.
点评:此题主要考查了二次根式的混合运算,在加减的过程中,有同类二次根式的要合并注意认真计算防止出错.
8、(2011•南京)如图,过正五边形ABCDE的顶点A作直线l∥CD,则∠1= 36° .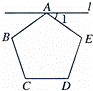
考点:平行线的性质;多边形内角与外角。
专题:推理填空题。
分析:由已知l∥CD,所以∠1=∠2,又由正五边形ABCDE得∠BAE=540°÷5=108°,从而求出∠1的度数.
解答:解:∵l∥CD,正五边形ABCDE,
∴∠1=∠2,
∠BAE=540°÷5=108°,
∴∠1=∠2=180°﹣∠BAE,
即2∠1=180°﹣108°,
∴∠1=36°.
故答案为:36°.
点评:此题考查的知识点是平行线的性质及正多边形的性质,解题的关键是由正多边形的性质和已知得出答案.
7、(2011•南京)﹣2的相反数是 2 .
考点:相反数。
分析:一个数的相反数就是在这个数前面添上“﹣”号.﹣2的相反数是2.
解答:解:﹣2的相反数是2.
点评:本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号.一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.
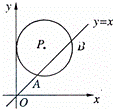
6、(2011•南京)如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为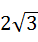 ,则a的值是( )
,则a的值是( )
A、2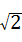 B、2+
B、2+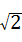
C、2 D、2+
D、2+
考点:一次函数综合题。
专题:综合题。
分析:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PO,PA.分别求出PD、DC,相加即可.
解答:解:过P点作PE⊥AB于E,过P点作PC⊥x轴于C,交AB于D,连接PO,PA.
∵AE=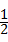 AB=
AB= ,PA=2,
,PA=2,
PE=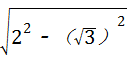 =1.
=1.
PD=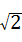 .
.
∵⊙P的圆心是(2,a),
∴DC=2,
∴a=PD+DC=2+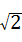 .
.
故选B.
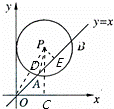
点评:本题综合考查了一次函数与几何知识的应用,题中运用圆与直线的关系以及直角三角形等知识求出线段的长是解题的关键.注意函数y=x与x轴的夹角是45°.
5、(2011•南京)如图是一个三棱柱.下列图形中,能通过折叠围成一个三棱柱的是( )
A、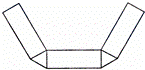 B、
B、
C、 D、
D、
考点:展开图折叠成几何体。
专题:几何图形问题。
分析:利用三棱柱及其表面展开图的特点解题.三棱柱上、下两底面都是三角形.
解答:解:A、折叠后有二个侧面重合,不能得到三棱柱;
B、折叠后可得到三棱柱;
C、折叠后有二个底面重合,不能得到三棱柱;
D、多了一个底面,不能得到三棱柱.
故选B.
点评:本题考查了三棱柱表面展开图,上、下两底面应在侧面展开图长方形的两侧,且都是三角形.
4、(2011•南京)为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的是( )
A、随机抽取该校一个班级的学生 B、随机抽取该校一个年级的学生
C、随机抽取该校一部分男生 D、分别从该校初一、初二、初三年级中各随机抽取10%的学生
考点:全面调查与抽样调查。
专题:应用题。
分析:本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
解答:解:因为要了解初中的视力情况范围较大、难度较大,所以应采取抽样调查的方法比较合适,
本题考查的是调查方法的选择,正确选择调查方式要根据全面调查的优缺点再结合实际情况去分析,
故只有D符合实际并具有普遍性,
故选D.
点评:本题考查了调查方法的选择,正确选择调查方式要根据全面调查的优缺点再结合实际情况去分析,难度适中.
3、(2011•南京)在第六次全国人口普查中,南京市常住人口约为800万人,其中65岁及以上人口占9.2%,则该市65岁及以上人口用科学记数法表示约为2%,则该市65岁及以上人口用科学记数法表示约为( )
A、0.736×106人 B、7.36×104人
C、7.36×105人 D、7.36×106人
考点:科学记数法-表示较大的数。
专题:计算题。
分析:先计算出该市65岁及以上人口数,然后用科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解答:解:该市65岁及以上人口:8000000×9.2%=736000(人)
将736 000人用科学记数法表示7.36×105人.
故选C.
点评:题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2、(2011•南京)下列运算正确的是( )
A、a2+a3=a5 B、a2•a3=a6
C、a3+a2=a D、(a2)3=a6
考点:幂的乘方与积的乘方;合并同类项;同底数幂的乘法。
专题:计算题。
分析:根据合并同类项法则、积的乘方和幂的乘方的法则运算.
解答:解:A、a2与a3不是同类项,不能合并,故本选项错误;
B、a2•a3=a2+3=a5≠a6,故本选项错误;
C、a3与a2不是同类项,不能合并,故本选项错误;
D、(a2)3=a2×3=a6,故本选项正确.
故选D.
点评:此题考查了幂的乘方与积的乘方、合并同类项等知识,属于基本题型.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com