21、(2011•南京)如图，将▱ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．

(1)求证：△ABF≌△ECF；

(2)若∠AFC=2∠D，连接AC、BE，求证：四边形ABEC是矩形．

考点：平行四边形的判定与性质；全等三角形的判定与性质；矩形的判定。

专题：证明题。

分析：(1)先由已知平行四边形ABCD得出AB∥DC，AB=DC，⇒∠ABF=∠ECF，从而证得△ABF≌△ECF；

(2)由(1)得的结论先证得四边形ABEC是平行四边形，通过角的关系得出FA=FE=FB=FC，AE=BC，得证．

解答：证明：(1)∵四边形ABCD是平行四边形，

∴AB∥DC，AB=DC，

∴∠ABF=∠ECF，

∵EC=DC，∴AB=EC，

在△ABF和△ECF中，

∵∠ABF=∠ECF，∠AFB=∠EFC，AB=EC，

∴△ABF≌△ECF．

(2)∵AB=EC，AB∥EC，

∴四边形ABEC是平行四边形，

∴FA=FE，FB=FC，

∵四边形ABCD是平行四边形，

∴∠ABC=∠D，

又∵∠AFC=2∠D，

∴∠AFC=2∠ABC，

∵∠AFC=∠ABF+∠BAF，

∴∠ABF=∠BAF，

∴FA=FB，

∴FA=FE=FB=FC，

∴AE=BC，

∴四边形ABEC是矩形．

点评：此题考查的知识点是平行四边形的判定与性质，全等三角形的判定和性质及举行的判定，关键是先由平行四边形的性质证三角形全等，然后推出平行四边形通过角的关系证矩形．

20、(2011•南京)某校部分男生分3组进行引体向上训练．对训练前后的成绩进行统计分析，相应数据的统计图如下．

(1)求训练后第一组平均成绩比训练前增长的百分数；

(2)小明在分析了图表后，声称他发现了一个错误：“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%，所以第二组的平均成绩不可能提高3个这么多．”你同意小明的观点吗？请说明理由；

(3)你认为哪一组的训练效果最好？请提供一个解释来支持你的观点．

考点：条形统计图；扇形统计图。

专题：图表型。

分析：(1)用训练后的成绩减去训练前的成绩除以训练前的成绩乘以100%即可；

(2)求出第二组的平均成绩增加的个数与小明的说法相比较即可作出判断；

(3)可以从训练前后成绩增长的百分数去分析，也可以通过个数比较．

解答：解：(1)训练后第一组平均成绩比训练前增长的百分数是

×100%≈67%；

(2)我不同意小明的观点，因为第二组的平均成绩增加8×10%+6×20%+5×20%+0×50%=3个；

(3)本题答案不唯一，下列解法供参考．

我认为第一组的训练效果最好，因为训练后第一组的平均成绩比训练前增长的百分数最大．

点评：本题考查了条形统计图和扇形统计图的知识，解决此类题目的关键是正确的识图，通过正确的识图，从中整理出进一步解题的信息．

19、(2011•南京)解方程x²﹣4x+1=0．

考点：解一元二次方程-配方法；解一元二次方程-公式法。

分析：将原方程转化为完全平方的形式，利用配方法解答或利用公式法解答．

解答：解：(1)移项得，x²﹣4x=﹣1，

配方得，x²﹣4x+4=﹣1+4，

(x﹣2)²=3，

由此可得x﹣2=±，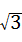

x₁=2+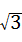，x₂=2﹣；

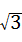(2)a=1，b=﹣4，c=1．

b²﹣4ac=(﹣4)2﹣4×1×1=12＞0．

x==2±，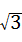

x₁=2+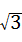，x₂=2﹣．

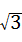点评：此题考查了解一元二次方程，解题时要注意解题步骤的准确应用．

(1)选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．

(2)选择公式法解一元二次方程时，找准a、b、c的值是关键．

18、(2011•南京)计算．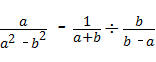

考点：分式的混合运算。

分析：首先把除法运算转化成乘法运算，然后找出最简公分母，进行通分，化简．

解答：解：原式=﹣•，

=﹣，

=+，

=，

=，

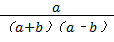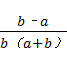点评：此题主要考查了分式的混合运算，通分、因式分解和约分是解答的关键．

17、(2011•南京)解不等式组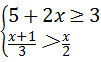，并写出不等式组的整数解．

考点：一元一次不等式组的整数解；解一元一次不等式组。

分析：首先解出两个不等式的解集，然后求出公共解集，找出符合条件的整数解即可．

解答：解：，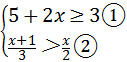

由①得：x≥﹣1，

由②得：x＜2，

∴不等式组的解集为：﹣1≤x＜2，

∴不等式组的整数解是：﹣1，0，1，

点评：此题主要考查了不等式组的解法，求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．

16、(2011•南京)甲、乙、丙、丁四位同学围成一圈依序循环报数，规定：

①甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5，乙报6…按此规律，后一位同学报出的数比前一位同学报出的数大1．当报到的数是50时，报数结束；

②若报出的数为3的倍数，则报该数的同学需拍手一次．在此过程中，甲同学需拍手的次数为　4　．

考点：规律型：数字的变化类。

分析：根据报数规律得出甲共报数13次，分别为1，5，9，13，17，21，25，29，33，37，41，45，49，即可得出报出的数为3的倍数的个数，即可得出答案．

解答：解：∵甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5，乙报6…按此规律，后一位同学报出的数比前一位同学报出的数大1．当报到的数是50时，报数结束；

∴50÷4=12余2，

∴甲共报数13次，分别为1，5，9，13，17，21，25，29，33，37，41，45，49，

∴报出的数为3的倍数，则报该数的同学需拍手一次．在此过程中，甲同学需拍手的次数为：9，21，33，45时，

所以一共有4次．

故答案为：4．

点评：此题主要考查了数字规律，得出甲的报数次数以及分别报数的数据是解决问题的关键．

15、(2011•南京)设函数y=与y=x﹣1的图象的交点坐标为(a，b)，则﹣的值为　﹣．

考点：反比例函数与一次函数的交点问题。

专题：计算题。

分析：把交点坐标代入2个函数后，得到2个方程，求得a，b的解，整理求得﹣的值即可．

解答：解：∵函数y=与y=x﹣1的图象的交点坐标为(a，b)，

∴b=，b=a﹣1，

∴=a﹣1，

a²﹣a﹣2=0，

(a﹣2)(a+1)=0，

解得a=2或a=﹣1，

∴b=1或b=﹣2，

∴则﹣的值为．

故答案为：．

点评：考查函数的交点问题；得到2个方程判断出a，b的值是解决本题的关键．

14、(2011•南京)如图，E、F分别是正方形ABCD的边BC、CD上的点，BE=CF，连接AE、BF．将△ABE绕正方形的中心按逆时针方向旋转到△BCF，旋转角为α( 0°＜α＜180°)，则∠α=　90°　．

考点：旋转的性质；全等三角形的判定与性质；正方形的性质。

分析：首先作出旋转中心，根据多边形的性质即可求解．

解答：解：∵四边形ABCD是正方形．

∴∠AOB=90°，

故α=90°．

故答案是：90°．

点评：本题主要考查了旋转的性质，以及正多边形的性质，正确理解正多边形的性质以及旋转角是解题的关键．

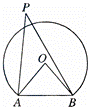
13、(2011•南京)如图，海边立有两座灯塔A、B，暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内，∠AOB=80°．为了避免触礁，轮船P与A、B的张角∠APB的最大值为　40°　．

考点：圆周角定理；三角形的外角性质。

分析：根据已知得出当P点在圆上时，轮船P与A、B的张角∠APB的最大，根据圆周角定理得出答案．

解答：解：∵海边立有两座灯塔A、B，暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内，∠AOB=80°．

∴当P点在圆上时，轮船P与A、B的张角∠APB的最大，

此时为∠AOB=80°的一半，为40°．

故答案为：40°．

点评：此题主要考查了圆周角定理的应用，根据条件得出当P点在圆上时，轮船P与A、B的张角∠APB的最大是解决问题的关键．

12、(2011•南京)如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD的面积为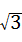　2cm²．

考点：菱形的性质；勾股定理。

分析：因为DE丄AB，E是AB的中点，所以AE=1cm，根据勾股定理可求出BD的长，菱形的面积=底边×高，从而可求出解．

解答：解：∵E是AB的中点，

∴AE=1，

∵DE丄AB，

∴DE==．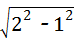

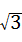∴菱形的面积为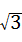：2×=2．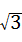

故答案为：2．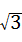

点评：本题考查菱形的性质，四边都相等，菱形面积的计算公式以及勾股定理的运用等．