
题目列表(包括答案和解析)
4.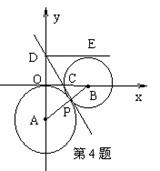 (甘肃)如图,在直角坐标系xoy中,以点A(0,-3)为圆心
(甘肃)如图,在直角坐标系xoy中,以点A(0,-3)为圆心
作圆与x轴相切,⊙B与⊙A外切于点P,B点在x轴正半轴上,
过P点作两圆 的公切线DP交y轴于D,交x轴于C
.(1)设⊙A的半径为r1,⊙B的半径为r2,且r2=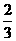 r1,求公切线
r1,求公切线
DP的长及直线DP的函数解析式;(2)若⊙A的位置,大小不变,
点B在x轴正半轴上移动,⊙B与⊙A始终外切,过D作⊙B
的切线DE ,E为切点,当DE=4时,B点在什么位置?从解答中能发现什么?
3.(甘肃)如图;在△ABC 中,AB=4,BC=3,∠B=90°,
点D在AB上运动,但与A、B不重合,过B、C、D
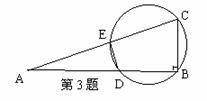 三点的圆交AC于E ,连结DE.(1)设AD=x,CE=y,求y与x之间的
三点的圆交AC于E ,连结DE.(1)设AD=x,CE=y,求y与x之间的
函数关系式,并指出自变量x的取值范围;
(2)当AD长为关于x的方程2x2+(4m+1)x+2m=0的一个
整数根时,求m的值.
2.(辽宁)已知:如图,P与x轴相交于坐标原点O,点A(0,2)
是P与y轴的交点,点B(-2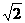 ,0)在x轴上,连结BP交P于
,0)在x轴上,连结BP交P于
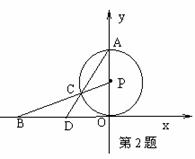 点C,连结AC并延长交x轴于点D.
点C,连结AC并延长交x轴于点D.
(1)求线段BC的长;(2)求直线AC的函数解析式;
(3)当点B在x轴上移动时,是否存在点B,使△BOP相
似于△AOD?若存在,求出符合条件的坐标;若不存在,说明理由.
1.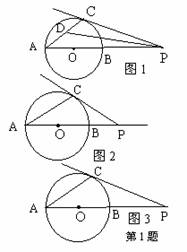 (北京)已知:AB为⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,设切点P作⊙O的切线,设切点为C.
(北京)已知:AB为⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,设切点P作⊙O的切线,设切点为C.
(1)当点P在AB延长线上的位置如图1所示时,连结AC,作
∠APC的平分线,交AC于点D,请你测量出∠CDP的度数;
(2)当点P在AB延长线上的位置如图2和图3所示时,连
结AC,请你分别在这两个图中用尺规作∠APC的平分线
(不写作法,保留作图痕迹),设此角平分线交AC于点D,
然后在这两个图中分别测量出∠CDP的度数.猜想:
∠CDP的度数是否随点P在AB延长线上的位置的变
化而变化?请对你的猜想加以证明.
29.(本题满分10分)
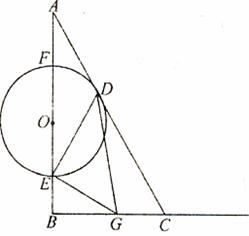
已知:如图,RtΔABC中,∠B=90º,∠A=30º,BC=6cm.点O从A点出发,沿AB以每秒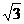 cm的速度向B点方向运动,当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与边AB相交于E、F两点.过E作EG⊥DE交射线BC于G.
cm的速度向B点方向运动,当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与边AB相交于E、F两点.过E作EG⊥DE交射线BC于G.
⑴若E与B不重合,问t为何值时,ΔBEG与ΔDEG相似?
⑵问:当t在什么范围内时,点G在线段BC上?当t在什么范围内时,点G在线段BC的延长线上?
⑶当点G在线段BC上(不包括端点B、C)时,求四边形CDEG的面积S(cm2)关于时间t(秒)的函数关系式,并问点O运动了几秒钟时,S取得最大值?最大值为多少?
28.(本题满分10分)
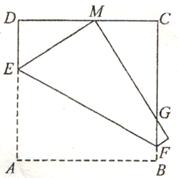
将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图).
⑴如果M为CD边的中点,求证:DE∶DM∶EM=3∶4∶5;
⑵如果M为CD边上的任意一点,设AB=2a,问ΔCMG的周长是否与点M的位置关系?若有关,请把ΔCMG的周长用含DM的长x的代数式表示;若无关,请说明理由.
27.(本题满分9分)
已知直线y=-2x+b(b≠0)与x轴交于点A,与y轴交于点B;一抛物线的解析式为
y=x2-(b+10)x+c.
⑴若该抛物线过点B,且它的顶点P在直线y=-2x+b上,试确定这条抛物线的解析式;⑵过点B作直线BC⊥AB交x轴于点C,若抛物线的对称轴恰好过C点,试确定直线
y=-2x+b的解析式.
26.(本题满分8分)
西北某地区为改造沙漠,决定从2002年起进行“治沙种草”,把沙漠地变为草地,并出台了一项激励措施:在“治沙种草”过程中,每一年新增草地面积达到10亩的农户,当年都可得到生活补贴费1500元,且每超出一亩,政府还给予每亩a元的奖励.另外,经治沙种草后的土地从下一年起,平均每亩每年可有b元的种草收入.下表是某农户在头两年通过“治沙种草”每年获得的总收入情况:
|
年 份 |
新增草地的亩数 |
年总收入 |
|
2002年 |
20亩 |
2600元 |
|
2003年 |
26亩 |
5060元 |
(注:年总收入=生活补贴费+政府奖励费+种草收入)
⑴试根据以上提供的资料确定a,b的值;
⑵从2003年起,如果该农户每年新增草地的亩数均能比前一年按相同的增长率增长,那么2005年该农户通过“治沙种草”获得的年总收入将达到多少元?
25.(本题共有2题,每题6分,满分12分)
读一读,想一想,做一做:
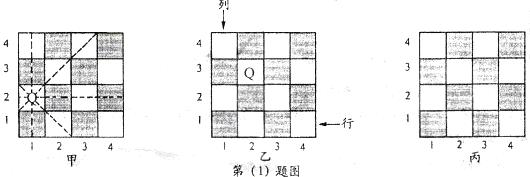
⑴国际象棋、中国象棋和围棋号称为世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
① 在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“(2,3)”来表示,请说明“皇后Q”所在的位置“(2,3)”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置.
② 如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互相不受对方控制(在图丙中的某四个小方格中标出字母Q即可).
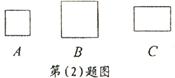
⑵现有足够的2×2,3×3的正方形和2×3的矩形图片A、B、C(如图),现从中各选取若干个图片拼成不同的图形.请你在下面给出的方格纸中,按下列要求分别画出一种拼法示意图(说明:下面给出的方格纸中,每个小正方形的边长均为1.拼出的图形,要求每两个图片之间既无缝隙,也不重叠.画图必须保留拼图的痕迹).
①选取A型、B型两种图片各1块,C型图片2块,在下面的图1中拼成一个正方形;
 ②选取A型图片4块,B型图片1块,C型图片4块,
②选取A型图片4块,B型图片1块,C型图片4块,
在下面的图2中拼成一个正方形;
③选取A型图片3块,B型图片1块,再选取若干块
C型图片,在下面的图3中拼成一个矩形.

24.(本题满分6分)
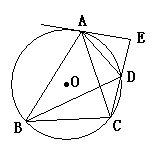
已知:如图,四边形ABCD内接于⊙O,过点A的切线与CD的延长线交于E,
且∠ADE=∠BDC.
⑴求证:ΔABC为等腰三角形;
⑵若AE=6,BC=12,CD=5,求AD的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com