7．如图，正方形的面积是144，则阴影部分面积的小正方形边长是　　　　　 。

6．二次函数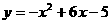，对称轴是__________________。

5．一个口袋中装有4个白球，1个红球，7个黄球，搅匀后随机从袋中摸出1个球是白球的概率是__________ 。

4．函数中，自变量的取值范围是　　　　　　 。

3．分解因式：　　　　　　　　 　。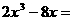

2．“世界银行全球扶贫大会”于2004年5月26日在上海开幕.从会上获知，我国国民生产总值达到11.69万亿元，人民生活总体上达到小康水平，其中11.69万亿用科学记数法表示应为　　　　　 　　　　　亿元。

1．-6的绝对值是　　　　 ；8的平方根是　　　　 　；-1的相反数是　　　　 　。

30．(本题9分) 如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为(3，0)，(3，4).动点M、N分别从O、B同时出发，以每秒1个单位的速度运动。其中，点M沿OA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥BC，交AC于P，连结MP. 已知动点运动了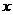秒。

(1)P点的坐标为(　　　　　　 ，　　　　　　　 )；(用含x的代数式表示)

(2)试求 △MPA面积的最大值，并求此时x的值。

(3)请你探索：当x为何值时，△MPA是一个等腰三角形？

你发现了几种情况？写出你的研究成果。

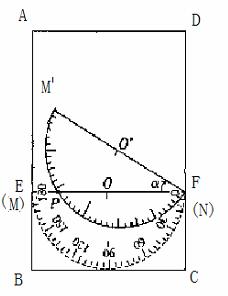
29．(本题7分) 如图，在矩形ABCD中，AB=3，AD=2，点E、F分别在AB、DC上，AE=DF=2.再把一块直径为2的量角器(圆心为O)放置在图形上，使其0°线MN与EF重合；若将量角器0°线上的端点N固定在点F上，再把量角器绕点F顺时针方向旋转∠α(0°<α<90°),此时量角器的半圆弧与EF相交于点P，设点P处量角器的读数为°.

(1)用含°的代数式表示∠α的大小；

(2)当°等于多少时，线段PC与平行？

28．(本题9分) 某地区为了改善生态环境，防止水土流失，决定从2003年起开始“退耕还林”，在山坡上推广种植某种果树，并且出台了一项激励措施：在“退耕还林”的过程中，每一年新增果树达到100棵的农户，当年都可得到生活补贴1200元，且每超出一棵，政府还给予每棵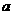元的奖励．另外，种植的果树，从下一年起，每年每棵平均将有元的果实收入．

下表是某农户在头两年通过“退耕还林”每年获得的总收入情况：

(注：年总收入＝生活补贴费+政府奖励费+果实收入)

(1)试根据以上提供的资料确定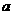、的值；

(2)从2005年起，该农户每年新增果树的棵数将以某一百分率增长，预计2006年新增果树216棵，那么2006年该农户通过“退耕还林”获得的年总收入将达到多少元？