
题目列表(包括答案和解析)
4.有6张背面相同的扑克牌,正面上的数字分别是4,5,6,7,8,9.若将这六张牌背面朝上洗匀后,从中任意抽取一张,那么这张牌正面上的数字是9的概率为( ).
(A) 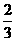 (B)
(B) 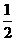 (C)
(C) 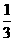 (D)
(D) 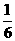
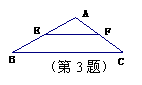
3. 如图所示,BC=6,E、F分别是线段AB和线段AC的中点,
那么线段EF的长是( ).
(A)6 (B)5 (C)4.5 (D)3
2.化简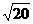 的结果是( ).
的结果是( ).
 (A)
(A)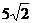 (B)
(B)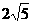 (C)
(C) 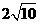 . (D)
. (D)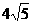
1. 图中物体的形状类似于( ).
图中物体的形状类似于( ).
(A)棱柱 (B)圆柱 (C)圆锥 (D)球
(第1题)
28.(本题满分14分)
如图1,AB是⊙O的直径,射线BM⊥AB,垂足为B,点C为射线BM上的一个动点(C与B不重合),连结AC交⊙O于D,过点D作⊙O的切线交BC于E。
(1)在C点运动过程中,当DE∥AB时(如图2),求∠ACB的度数;
(2)在C点运动过程中,试比较线段CE与BE的大小,并说明理由;
(3)∠ACB在什么范围内变化时,线段DC上存在点G,满足条件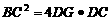 (请写出推理过程)。
(请写出推理过程)。

图1 图2
27.(本题满分12分)
已知:抛物线 的图象经过点(1,0),一条直线
的图象经过点(1,0),一条直线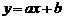 ,它们的系数之间满足如下关系:
,它们的系数之间满足如下关系: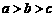 。
。
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作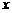 轴的垂线,垂足分别为A1、B1。令
轴的垂线,垂足分别为A1、B1。令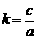 ,试问:是否存在实数
,试问:是否存在实数 ,使线段A1B1的长为
,使线段A1B1的长为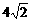 。如果存在,求出
。如果存在,求出 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
26.(本题满分12分)
若一个矩形的短边与长边的比值为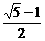 (黄金分割数),我们把这样的矩形叫做黄金矩形。
(黄金分割数),我们把这样的矩形叫做黄金矩形。
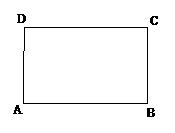
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD;
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由;
(3)归纳:通过上述操作及探究,请概括出具有一般性的结论(不需要证明)。
25.(本题12分)近几年,扬州先后获得了“中国优秀旅游城市”和“全国生态建设示范城市”等十多个殊荣。到扬州观光旅游的客人越来越多,某景点每天都吸引大量的游客前来观光。事实表明,如果游客过多,不利于保护珍贵文物,为了实施可持续发展,兼顾社会效益和经济效益,该景点拟采用浮动门票价格的方法来控制游览人数。已知每张门票原价为40元,现设浮动门票为每张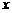 元,且
元,且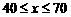 ,经市场调研发现一天游览人数
,经市场调研发现一天游览人数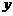 与票价
与票价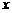 之间存在着如图所示的一次函数关系。
之间存在着如图所示的一次函数关系。
(1)根据图象,求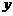 与
与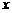 之间的函数关系式;
之间的函数关系式;
(2)设该景点一天的门票收入为 元。
元。
①试用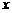 的代数式表示
的代数式表示 ;
;
②试问:当门票定为多少时,该景点一天的门票收入最高?最高门票收入是多少?

24.(本题满分12分)
为配和新课程的实施,某市举行了“应用与创新”知识竞赛,共有1万名学生参加了这次竞赛(满分100分,得分全为整数)。为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
|
组别 |
分 组 |
频
数 |
频率 |
|
1 |
49.5-59.5 |
60 |
0.12 |
|
2 |
59.5-69.5 |
120 |
0.24 |
|
3 |
69.5-79.5 |
180 |
0.36 |
|
4 |
79.5-89.5 |
130 |
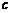 |
|
5 |
89.5-99.5 |
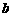 |
0.02 |
|
合 计 |
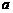 |
1.00 |
解答下列问题:
(1)在这个问题中,总体是 ,
样本容量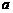 =
;
=
;
(2)第四小组的频率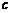 =
;
=
;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计全市获一等奖的人数。
23.(本题满分10分)
若反比例函数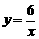 与一次函数
与一次函数 的图象都经过点A(
的图象都经过点A(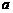 ,2)
,2)
(1)求点A的坐标;
(2)求一次函数 的解析式;
的解析式;
(3)设O为坐标原点,若两个函数图像的另一个交点为B,求△AOB的面积。
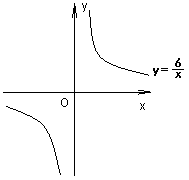
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com