27.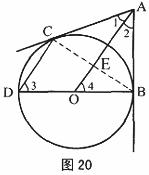解：(1)连结BC交OA于点E　 ……………………………1分

　　　　　 ∵AB、AC是⊙O的切线，

　　　　　 ∴AB＝AC，∠1＝∠2，

　　　　　 ∴AE⊥BC.

　　　　　 ∴∠OEB＝90°　　 ……………………………2分

　　　　　 ∵BD是⊙O的直径，

　　　　　 ∴∠DCB＝90°.

　　　　　 ∴∠DCB＝∠OEB.

　　　　　 ∴CD∥AO.　　　　 ……………………………3分

　 (2)∵CD∥AO，

　　　　 ∴∠3＝∠4.

　　　　 ∵AB是⊙O的切线，DB是直径，

　　　　 ∴∠BCD＝∠ABO＝90°.

　　　　 ∴△BDC∽△AOB.　　 ……………………………4分

　　　 　∴，

　　　　 ∴ .

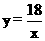　　　　 ∴　　　　　 ……………………………5分

　　　　 ∴0＜x＜6　　　　　 ……………………………6分

　 (3)由已知和(2)知 　…………………………… 8分

　　　 解这个方程组得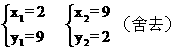：…………………………… 9分

　　　 ∴AB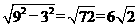＝.　　　　 …………………………… 10分

26．解：(1)样本容量：50　　 优秀率：34%　　 频数：4　 频率：0.18 …………每空1分，共4分

　 　　(2)中位数落在84－95.5这一分数段内。………………………………………………6分

　　　 (3)略。评分说明：只要选择了两个方面作答，分析合理 ……………………………8分

　　　　　　 叙述准确，用语精练，体现用样本估计总体的思想。 ……………………………9分

25.解：(1)当CE＝4时，四边形ABED是等腰梯形。…………1分

　　　　　 理由如下：

　　　 　　在BC上截取CE＝AD，连结DE、AE，

　　　　　 ∵AD∥BC，

　　　　　 ∴四边形AECD是平行四边形。……………………2分

　　　　　 ∴AE＝CD＝BD。

　　　　　 ∵BE＝12－4＝8＞4，即BE＞AD，

　　　　　 ∴AB不平行于DE，

　　　　　 ∴四边形ABED是梯形。　　 ……………………3分

　　　　　 ∵AE∥CD，CD＝BD，

　　　　　 ∴∠AEB＝∠C＝∠DBC。

　　　　　 在△ABE和△DEB中，

　　　　　 ∴△ABE≌△DEB (SAS)。

　　　　　 ∴AB＝DE，

　　　　　 ∴四边形ABED是等腰梯形。……………………5分

　 (也可不作辅助线，通过证明△ABD≌EDC而得AB＝DE)

　　　 (2)当C＝6时，四边形ABD是直角梯形。……………………6分

　　　　　 理由如下：

　　　　　 在BC上取一点，使C＝B＝＝6，连结D，

　　　　　 ∵BD＝CD

　　　　　 ∴D⊥BC

　　　　 又∵B≠AD，AD∥B，

　　　　　 ∴AB不平行于D　 …………………………………………7分

　　　　　 ∴四边形ABD是直角梯形。………………………………8分

24．解：设李师傅的平均速度为x千米/时，则张师傅的平均速度为(x－20)千米/时。

　　　　 根据题意，得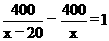 ………………………………………………………(3分)

　　　　 去分母，整理，得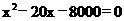

　　　　　　　　 　………………………………………………………(4分)

　　　　 经检验，都是所列方程的根，但不符合题意，舍去。

　　　　　　　 ∴ x＝100　　　　　　　 ………………………………………………………(5分)

　　　　 ∴李师傅的最大时速是：100(1+10%)＝110　　 …………………………………(6分)

　　　　 ∴李师傅行驶途中的最大时速在限速范围内，他没有超速违法。 …………………(7分)

23．解：(1)图16能反映y与x之间的函数关系。……………………………………………(1分)

　　　　　 从图中可以看出存入的本金是100元。……………………………………………(2分)

　　　　　 一年后的本息和是102.25元。………………………………………………………(3分)

　　　　 (2)设y与x之间的函数关系式为：y＝100·n%x+100 …………………………(4分)

　　　　　　 把(1，102.25)代入上式，得

　　　　　　　 n＝2.25

　　　　　　 ∴y＝2.25x+100　　　 ……………………………………………………………(5分)

　　　　　 当x＝2时，y＝2.25×2+100＝104.5(元)………………………………………(6分)

22. 解：

21．解：原式＝2+1－3　 ………………………………(做对一个部分得1分)(3分)

　　　　　　 ＝0　　　 ……………………………………………………………(4分)

17.　 18.　 3858　　 19. 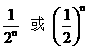　20.

13. 1　　　　 14.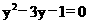　 15. 30　　　　　　　　　　　　　　　 16.外离

9.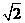 　　　　10. ±12xy　　　 　　11. ∠B＝∠D或∠C＝∠E或AC＝AE　　　 12. 15