
题目列表(包括答案和解析)
有一项是符合题目要求的)
1. 2的倒数是
A. B.
B.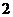 C.
C.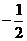 D.
D.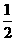
30.(本题10分)
 已知:抛物线y=- x2-(m+3)x+m2-12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
已知:抛物线y=- x2-(m+3)x+m2-12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
(1)求抛物线的解析式;
(2)在x轴上,点A的左侧,求一点E,使△ECO与△CAO相似,并说明直线EC经过(1)中抛物线的顶点D;
(3)过(2)中的点E的直线y= x+b与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M'、N',点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q.是否存在t值,使S梯形 MM'N'N:S△QMN=35:12,若存在,求出满足条件的t值;若不存在,请说明理由.
x+b与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M'、N',点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q.是否存在t值,使S梯形 MM'N'N:S△QMN=35:12,若存在,求出满足条件的t值;若不存在,请说明理由.
29.(本题9分)
如图:已知,△ABC内接于⊙O,弦BC所对的劣弧为1200,∠ABC、∠ACB的平分线BD、CE分别交AC于D,交AB于E,BD、CE相交于点F.
(1)求cot∠EFB的值;
(2)EF=DF;
(3)当BF=3EF,且线段BF、CF的长是关于x的方程x2-(2m+6)x+2m2=0(m>0)的两个实数根时,求AB的长.
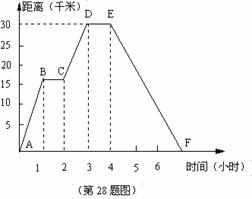

28.(本题6分)
小明同学骑自行车去郊外春游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
(1)根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?
(2)求小明出发两个半小时离家多远?
(3)求小明出发多长时间距家12千米?
27.(本题6分)
“利海”通讯器材商场,计划用60000元从厂家购进若干部新型手机,以满足市场需求,已知该厂家生产三种不同型号的手机,出厂价分别为甲种型号手机每部1800元,乙种型号手机每部600元,丙种型号手机每部1200元.
(1)若商场同时购进其中两种不同型号的手机共40部,并将60000元恰好用完.请你帮助商场计算一下如何购买.
(2)若商场同时购进三种不同型号的手机共40部,并将60000元恰好用完,并且要求乙种型号手机的购买数量不少于6部且不多于8部,请你求出商场每种型号手机的购买数量.
26.(本题6分)
如图:⊙O1与⊙O2外切于点P,O1O2的延长线交⊙O2于点A,AB切⊙O1于点B,交⊙O2于点C,BE是⊙O1的直径,过点B作BF┴O1P,垂足为F,延长BF交PE于点G.
 (1)求证:PB2=PG·PE;
(1)求证:PB2=PG·PE;
(2)若PF= ,tan∠A=
,tan∠A= ,求:O1O2的长.
,求:O1O2的长.
25.(本题5分)
中小学生的视力状况受到全社会的广泛关注,某市有关部门对全市4万名初中生的视力状况进行一次抽样调查统计,所得到的有关数据绘制成频率分布直方图,如下图,从左至右五个小组的频率之比依次是2:4:9:7:3,第五小组的频数是30.
(1)本次调查共抽测了多少名学生?
(2)本次调查抽测的数据的中位数应在哪个小组?说明理由.
(3)如果视力在4.9-5.1(含4.9、5.1)均属正常,那么全市初中生视力正常的约有多少人?


24.(本题5分)
如图,在测量塔高AB时,选择与塔底在同一水平面的同一直线上的C、D两点,用测角仪器测得塔顶A的仰角分别是300和600.已知测角仪器高CE=1.5米,CD=30米.
求塔高AB.(答案保留根号)
23.(本题4分)
|
如图,已知E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,
连结AE,分别交BC、BD于点F、G,连结AC交BD于O,连结OF.
求证:AB=2OF.
22.(本题5分)
用换元法解方程:x2+2x-2= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com