
题目列表(包括答案和解析)
3. 下列计算中,正确的是
A.2a+3b=5ab B.a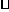 a3=a3
a3=a3
C.a6÷a2=a3 D.(-ab)2=a2b2
2. 图1中几何体的主视图是
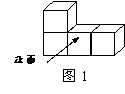




有一项是符合题目要求的)
1. 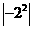 的值是
的值是
A.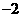 B.
B. C.
C. D.
D.
28. (本小题满分12分)
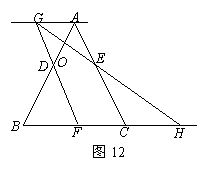 已知:如图12,等边三角形ABC的边长为6,点D,E分别在边AB,AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.
已知:如图12,等边三角形ABC的边长为6,点D,E分别在边AB,AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.
(1)设△EGA的面积为S,写出S与t的函数关系式;
(2)当t为何值时,AB⊥GH;
(3)请你证明△GFH的面积为定值;
(4)当t为何值时,点F和点C是线段BH的三等分点.
27. (本小题满分12分)
光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.
两地区与该农机租赁公司商定的每天的租赁价格见下表:
|
|
每台甲型收割机的租金 |
每台乙型收割机的租金 |
|
A地区 |
1800元 |
1600元 |
|
B地区 |
1600元 |
1200元 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说
明有多少种分派方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提
出一条合理建议.
26. (本小题满分12分)
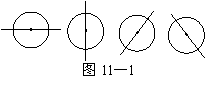 我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图11-1).
我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图11-1).
探索下列问题:
(1)在图11-2给出的四个正方形中,各画出一
条直线(依次是:水平方向的直线、竖直方
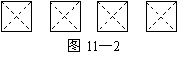 向的直线、与水平方向成45°角的直线和
向的直线、与水平方向成45°角的直线和
任意的直线),将每个正方形都分割成面积
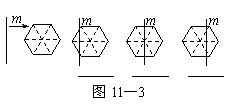 相等的两部分;
相等的两部分;
(2)一条竖直方向的直线m以及任意的直线n,
在由左向右平移的过程中,将正六边形分成
左右两部分,其面积分别记为S1和S2.
①请你在图11-3中相应图形下方的横线上
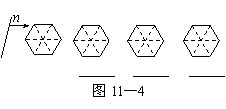 分别填写S1与S2的数量关系式(用“<”,
分别填写S1与S2的数量关系式(用“<”,
“=”,“>”连接);
②请你在图11-4中分别画出反映S1与S2
三种大小关系的直线n,并在相应图形下
方的横线上分别填写S1与S2的数量关系
式(用“<”,“=”,“>”连接).
 (3)是否存在一条直线,将一个任意的平面图形(如图11-5)分割成面积相等的两部分?请简略说出理由.
(3)是否存在一条直线,将一个任意的平面图形(如图11-5)分割成面积相等的两部分?请简略说出理由.
25. (本小题满分12分)
 如图10-1是某段河床横断面的示意图.查阅该
如图10-1是某段河床横断面的示意图.查阅该
河段的水文资料,得到下表中的数据:
|
x(米) |
5 |
10 |
20 |
30 |
40 |
50 |
|
y(米) |
0.125 |
0.5 |
2 |
4.5 |
8 |
12.5 |
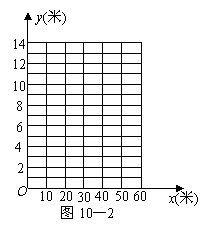 (1)请你以上表中的各对数据(x,y)作为点的坐标,
(1)请你以上表中的各对数据(x,y)作为点的坐标,
尝试在图10-2所示的坐标系中画出y关于x的
函数图象;
(2)①填写下表:
|
x |
5 |
10 |
20 |
30 |
40 |
50 |
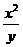 |
|
|
|
|
|
|
②根据所填表中数据呈现的规律,猜想出用x表示y
的二次函数的表达式: .
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能
否在这个河段安全通过?为什么?
24. (本小题满分8分)
如图9-1,一个圆球放置在V形架中.图9-2是它的平面示意图,CA和CB都是⊙O
的切线,切点分别是A,B.如果⊙O的半径为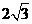 cm,且AB=6cm,求∠ACB.
cm,且AB=6cm,求∠ACB.
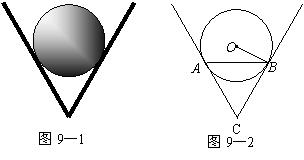
23. (本小题满分8分)
为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动.
初中三个年级根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分为100分)如下表所示:
|
|
决赛成绩(单位:分) |
|
初一年级 |
80 86 88 80 88 99 80 74 91 89 |
|
初二年级 |
85 85 87 97 85 76 88 77 87 88 |
|
初三年级 |
82 80 78 78 81 96 97 88 89 86 |
(1)请你填写下表:
|
|
平均数 |
众数 |
中位数 |
|
初一年级 |
85.5 |
|
87 |
|
初二年级 |
85.5 |
85 |
|
|
初三年级 |
|
|
84 |
(2)请从以下两个不同的角度对三个年级的决赛成绩进行分析:
① 从平均数和众数相结合看(分析哪个年级成绩好些);
② 从平均数和中位数相结合看(分析哪个年级成绩好些).
(3)如果在每个年级参加决赛的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些?并说明理由.
22. (本小题满分8分)
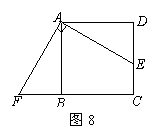 已知:如图8,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF.
已知:如图8,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF.
求证:DE=BF.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com