
题目列表(包括答案和解析)
1.下列各组数中,互为相反数的是( )
A.2与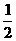 B.
B.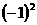 与1 C.-1与
与1 C.-1与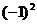 D.2与|-2|
D.2与|-2|
29、 (本题满分10分)
(本题满分10分)
如图,已知AB是⊙O的直径,AC是⊙O的弦,点D是ABC的中点,弦DE⊥AB,垂足为F,DE交AC于点G.
(1)图中有哪些相等的线段?(要求:不再标注其他字母,找结论的过程中所作的辅助线不能出现在结论中,不写出推理过程)
(2)若过点E作⊙O的切线ME,交AC的延长线于点M(请补完整图形),试问:ME=MG是否成立?若成立,请证明;若不成立,请说明理由.
 (3)在满足第(2)问的条件下,已知AF=3,FB=
(3)在满足第(2)问的条件下,已知AF=3,FB=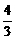 ,求AG与GM的比.[第(1)的结论可直接利用]
,求AG与GM的比.[第(1)的结论可直接利用]
28、(本题满分8分)
如图,在△ABC中,∠C=90°,AC=6,BC=8,M是BC的中点,P为AB上的一个动点,(可以与A、B重合),并作∠MPD=90°,PD交BC(或BC的延长线)于点D.
(1)记BP的长为x,△BPM的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(2)是否存在这样的点P,使得△MPD与△ABC相似?若存在,请求出x的值;若不存在,请说明理由.

27、(本题满分8分)

 在一块长16m、宽12m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半. 下面分别是小明和小颖的设计方案.
在一块长16m、宽12m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半. 下面分别是小明和小颖的设计方案.
小明说:我的设计方案如图(1),其中花园四周小路的宽度相等. 通过解方程,我得到小路的宽为2m或12m.
小颖说:我的设计方案如图(2),其中花园中每个角上的扇形相同.
(1)你认为小明的结果对吗?请说明理由.
(2)请你帮助小颖求出图中的x(精确到0.1m).
 (3)你还有其他的设计方案吗?请在下边的矩形中画出你的设计草图,并加以说明.
(3)你还有其他的设计方案吗?请在下边的矩形中画出你的设计草图,并加以说明.
26、(本题满分8分)
某市的一家报刊摊点从报社买进一种晚报,其价格为每份0.30元,卖出的价格为0.50元,卖不掉的报纸可以退还给报社,不过每份退还的钱数与退还的报纸的数量关系如下:
|
退还的数量 |
5 |
10 |
15 |
20 |
25 |
30或30以上 |
|
价格(元/份) |
0.25 |
0.20 |
0.15 |
0.10 |
0.05 |
0.02 |
现经市场调查发现,在一个月中(按30天记数)有20天可卖出150份/天,有10天只能卖出100份/天,而报社规定每天批发给摊点的报纸的数量必须相同.
(1)通过在坐标系中(以退还的钱数为纵坐标,退还的报纸数量为横坐标)描出点,分析出退还的钱数y(元)与退还的报纸数量k(份)之间的函数关系式.
(2)若该家报刊摊点每天从报社买进的报纸数x份(满足100<x<150),则当买进多少报纸时,毛利润最大?最多可赚多少钱?
25、(本题满分8分)
某校每学期都要对优秀的学生进行表扬,而每班采取民主投票的方式进行选举,然后把名单报到学校. 若每个班级平均分到3位三好生、4位模范生、5位成绩提高奖的名额,且各项均不能兼得. 现在学校有30个班级,平均每班50人.
(1)作为一名学生,你恰好能得到荣誉的机会有多大?
(2)作为一名学生,你恰好能当选三好生、模范生的机会有多大?
(3)在全校学生数、班级人数、三好生数、模范生数、成绩提高奖人数中,哪些是解决上面两个问题所需要的?
(4)你可以用哪些方法来模拟实验?
24、(本题满分6分)
夏雪同学调查了班级同学身上有多少零用钱,将每位同学的零用钱记录下来,下面是全班40名同学的零用钱的数目(单位:元)
2,5,0,5,2,5,6,5,0,5,5,52,5,8,0,5,5,2,5,
5,8,6,5,2,5,5,2,5,6,5,5,0,6,5,6,5,2,5,0.
(1)请你写出同学的零用钱(0元,2元,5元,6元8元)出现的频数;
(2)求出同学的零用钱的平均数、中位数和众数;
(3)假如老师随机问一个同学的零用钱,老师最有可能得到的回答是多少元?
23、(本题满分7分)
如图,给出五个条件:①AE平分∠BAD,②BE平分∠ABC,③E是CD的中点,④AE⊥EB,⑤AB=AD+BC
(1)请你以其中三个作为命题的条件,写出一个能推出AD∥BC的正确命题,并加以说明;
 (2)请你以其中三个作为命题的条件,写出一个不一定能推出AD∥BC的正确命题,并举例说明.
(2)请你以其中三个作为命题的条件,写出一个不一定能推出AD∥BC的正确命题,并举例说明.
22、(本题满分6分)
方格纸中每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.
(1)在10×10的方格中(每个小方格的边长为1个单位),画一个面积为1的格点钝角三角形ABC,并标明相应字母.
(2)再在方格中画一个格点△DEF,使得△DEF∽△ABC,且相似比为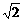 ,并加以证明.
,并加以证明.

21、(本题共有3小题,每小题5分,共15分)
(1)计算: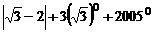
(2)已知不等式5(x-2)+8<6(x-1)+7的最小整数解是方程2x-ax=4的解,求a的值.
(3)先化简,再求值: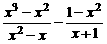 ,其中x=2.
,其中x=2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com