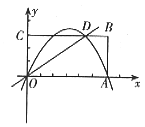
32、如图，已知直角坐标系内的梯形AOBC(O为原点)，AC∥OB，OC⊥BC，AC，OB的长是关于x的方程x²－(k+2)x+5=0的两个根，且S_△AOC：S_△BOC=1：5。

　 (1)填空：0C=________，k=________；

　 (2)求经过O，C，B三点的抛物线的另一个交点为D，动点P，Q分别从O，D同时出发，都以每秒1个单位的速度运动，其中点P沿OB由O→B运动，点Q沿DC由D→C运动，过点Q作QM⊥CD交BC于点M，连结PM，设动点运动时间为t秒，请你探索：当t为何值时，△PMB是直角三角形。

　 　33、矩形OABC在直角坐标系中的位置如图所示，A、C两点的坐标分别为A6，0)、C(0，3)，直线与BC边相交于点D。

　　 (1)求点D的坐标；

　　 (2)若抛物线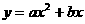经过D、A两点，试确定此抛物线的表达式；

　　 (3)P为x轴上方(2)中抛物线上一点，求△POA面积的最大值；

　　 (4)设(2)中抛物线的对称轴与直线OD交于点M，点Q为对称轴上一动点，以Q、O、M为顶点的三角形与△OCD相似，求符合条件的Q点的坐标。

31、已知，在矩形ABCD中，AB＝2，E为BC上一点，沿直线DE将矩形折叠，使C点落在AB边上的C¹点处，过作C¹H⊥DC，C¹H分别交DE、DC于点G、H，连结CG，C C¹，C C¹交GE于点F。

(1)　　　 求证：四边形CG C¹E为菱形；

(2)　　　 设，并设，试将y表示成x的函数

(3)　　　 当(2)中所求得的函数的图象达到最高点时，求BC的长。(江苏)

30、已知：抛物线的解析式为

(1)　　　 求证：此抛物线与x轴必有两个不同的交点；

(2)　　　 若此抛物线与直线的一个交点在y轴上，求m的值。

29、一张矩形纸片OABC平放在平面直角坐标系内，O为原点，点A在x的正半轴上，点C在y轴的正半轴上，OA＝5，OC＝4。

①求直线AC的解析式；

②若M为AC与BO的交点，点M在抛物线上，求k的值；

③将纸片沿CE对折，点B落在x轴上的点D处，试判断点D是否在②的抛物线上，并说明理由。(浙江)

28、一张矩形纸片OABC平放在平面直角坐标系内，O为原点，点A在x的正半轴上，点C在y轴的正半轴上，OA＝5，OC＝4。

①　如图，将纸片沿CE对折，点B落在x轴上的点D处，求点D的坐标；

②　在①中，设BD与CE的交点为P，若点P，B在抛物线上，求b，c的值；

③　若将纸片沿直线l对折，点B落在坐标轴上的点F处，l与BF的交点为Q，若点Q在②的抛物线上，求l 的解析式。(浙江)

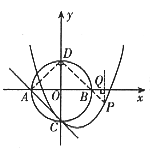
27、如图所示，在平面直角坐标系xOy中，半径为1的圆O分别交x轴、y轴于A、B、C、D四点，抛物线经过点C且与直线AC只有一个公共点。

　　 (1)求直线AC的解析式；

　　 (2)求抛物线的解析式；

(3)点P为(2)中抛物线上的点，由点P作x轴的垂线，垂足为点Q，问：此抛物线上是否存在这样的点P，使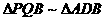？若存在，求出P点坐标；若不存在，请说明理由。(山西)

26、如图，边长为1的正方形OABC的顶点O为坐标原点，点A在x轴的正半轴上，点C在y轴的正半轴上．动点D在线段BC上移动(不与B，C重合)，连接OD，过点D作DE⊥OD，交边AB于点E，连接OE．记CD的长为t．

(1) 当t＝时，求直线DE的函数表达式；

(2) 如果记梯形COEB的面积为S，那么是否存在S的最大值？若存在，请求出这个最大值及此时t的值；若不存在，请说明理由；

(3) 当OD²+DE　²的算术平方根取最小值时，

求点E的坐标．(浙江)

25、教室里放有一台饮水机(如图)，饮水机上有两个放水管．课间同学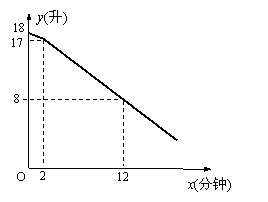们依次到饮水机前用茶杯接水．假设接水过程中水不发生泼洒，每个同学所接的水量都是相等的．两个放水管同时打开时，他们的流量相同.放水时先打开一个水管，过一会儿，再打开第二个水管，放水过程中阀门一直开着．饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示：

(1)求出饮水机的存水量y(升)与放水时间x(分钟)(x≥2)的函数关系式；(4分)

(2)如果打开第一个水管后，2分钟时恰好有4个同学接水结束，则前22个同学接水结束共需要几分钟？(4分)

(3)按(2)的放法，求出在课间10分钟内班级中最多有多少个同学能及时接完水？(4分)(江苏)

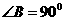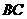24、有一个，，，，将它放在直角坐标系中，使斜边在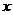轴上，直角顶点在反比例函数的图象上，求点的坐标．(常州)

23、如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2，0)，线段OA的长为6． 将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处．

⑴请在图中画出△COD;

⑵求点A旋转过程中所经过的路程(精确到0.1)；

⑶求直线BC的解析式(江苏)