8. 某圆锥的正视图是一个边长为的等边三角形，那么这个圆

　 锥的侧面积是______________.

7. 二次函数的图象的对

称轴是____________.

6. 如图，点D在以AC为直径的⊙O上，

如果∠BDC=20°，那么∠ACB的度数

为__________.

5. 反比例函数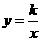的图象经过点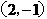，则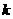的值为_________.

4. 某种禽流感病毒变异后的直径为米，将这个数写成科学记数法是____________________.

3. 函数y=中，自变量x的取值范围是__________.

2.. 分解因式：_______________.

1、的相反数为________;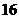的算术平方根是_________,计算的结果是_____

25.　　 (本小题满分12分)

如图15-1和15-2，在20×20的等距网格(每格的宽和高均是1个单位长)中，Rt△ABC从点A与点M重合的位置开始，以每秒1个单位长的速度先向下平移，当BC边与网的底部重合时，继续同样的速度向右平移，当点C与点P重合时，Rt△ABC停止移动.设运动时间为x秒，△QAC的面积为y.

(1)如图15-1，当Rt△ABC向下平移到Rt△A₁B₁C₁的位置时，请你在网格中画出Rt△A₁B₁C₁关于直线QN成轴对称的图形；

(2)如图15-2，在Rt△ABC向下平移的过程中，请你求出y与x的函数关系式，并说明当x分别取何值时，y取得最大值和最小值？最大值和最小值分别是多少？

(3)在Rt△ABC向右平移的过程中，请你说明当x取何值时，y取得最大值和最小值？最大值和最值分别是多少？为什么？

(说明：在(3)中，将视你解答方法的创新程度，给予1~4分的加分)

2004年河北省课程改革实验区初中毕业生学业考试

24.　　 (本小题满分10分)

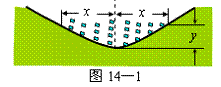如图14-1是某段河床横断面的示意图.查阅该河段的水文资料，得到下表中的数据：

(1)请你以上表中的各对数据(x，y)作为点的坐标，尝试在图14-2所示的坐标系中画出y关于x的函数图象；

(2)①填写下表：

x	5	10	20	30	40	50

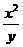　　　　 ②根据所填表中数据呈现的规律，猜想出用x表示y 的二次函数的表达式：　　　　　 　　　　　　　　.

(3)当水面宽度为36米时，一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过？为什么？