27如图16，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．

E为BC的中点，以OE为直径的⊙O′交轴于D点，过点D作DF⊥AE于点F．

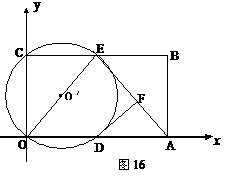(1) 求OA、OC的长；

解：

(2) 求证：DF为⊙O′的切线；

证明：

(3) 小明在解答本题时，发现△AOE是等腰三角形．由此，他断定：“直线BC上一定存在除点E以外的点P，使△AOP也是等腰三角形，且点P一定在⊙O′外”．你同意他的看法吗？请充分说明理由．

26．如示意图所示，边长为2的等边△ABC是三棱镜的一个横截面，一束光线沿着与AB边垂直的方向射入到BC边上的D点处(D点与B、C两点不重合)，反射光线又从AC边射出去．DK为法线．设BE的长为x，AF的长为y．

　(1)求y和x之间的函数关系式，并写出自变量x的取值范围；

　 (2)画出该函数的图象．

25．已知：二次函数的图象经过点A(－1，0)，B(0，－3)，对称轴方程为x＝1．

　(1)求此二次函数的解析式；

　(2)若以坐标原点O为圆心，4为半径作圆，判断点顶点P与⊙O的位置关系．

24、如图，有两个可以自由转动的转盘A、B，转盘A被均匀分成4等份，每份标上数字1、2、3、4四个数字；转盘B被均匀分成6等份，每份标上数字1、2、3、4、5、6六个数字。有人为甲乙两人设计了一个游戏，其规则如下：

(1)　　 同时转动转盘A与B；

(2)　　 转盘停止后，指针各指向一个数字(如果指针恰好指在分割线上，那么重转一次，直到指针指向一个数字为止)，用所指的两个数字作乘积，如果所得的积是偶数，那么甲得1分；如果所得的积是奇数，那么乙得1分。

你认为这样的规则是否公平？请你说明理由；如果不公平，请你设计一个公平的规则，并说明理由。

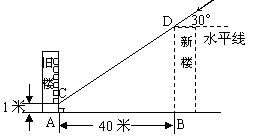
23、为解决楼房之间的挡光问题，某地区规定：两幢楼房间的距离至少为40米，中午12时不能挡光.如图，某旧楼的一楼窗台高1米，要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射，并且光线与水平线的夹角最小为30°，在不违反规定的情况下，请问新建楼房最高多少米？(结果精确到1米.，)

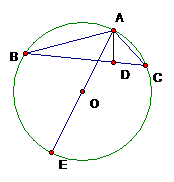
22．已知如图，在△ABC中，AB=6，AC=3，BC边上的高AD=2，

⊙O经过A，B，C三点，求⊙O的直径AE的长。

21.圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。

20、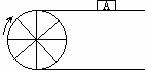如右图，当半径为30cm的转动轮转过120°角时，　　　 　　　　

传送带上的物体A平移的距离为　　 cm。

19．已知抛物线的顶点坐标为(2，3)，则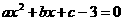的根是　　　　　　　　 。

18．如图18，⊙O是△ABC的内切圆，切点分别为E、F、G，若GC＝10，BF＝3，AG＝2，则△ABC为________三角形．