
题目列表(包括答案和解析)
27、(2004年湖北省襄樊)襄樊市认真落实国家关于减轻农民负担,增加农民收入的政策,从2003年开始减征农业税,2002年至2004年征收农业税变化情况见表(1),2004年市政府为了鼓励农民多种粮食,实行保护价收购,并对种植优质水稻(如中籼稻)另给予每亩15元的补贴(摘自《襄樊日报》2004年5月5日消息).我市农民李江家有4个劳动力,承包20亩土地,今年春季全部种植中籼稻和棉花,种植中籼稻和棉花每亩所需劳力和预计每亩平均产值见表(2).设2004年李江家种植中籼稻和棉花的预计总收入为P元,种植中籼稻的土地为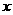 亩.
亩.
|
|
年份 |
2002 |
2003 |
2004 |
|
农业税(元/亩) |
117.24 |
70.44 |
38.26 |
|
|
农作物 |
产值(元/亩) |
劳力(人/亩) |
|
中籼稻 |
785 |
0.15 |
|
棉花 |
1200 |
0.35 |
(1) 李江家从国家开始减征农业税后两年可少交农业税多少元?
(2)
若不考虑上缴农业税,请写出P(元)与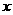 (亩)的函数关系式.
(亩)的函数关系式.
(3) 李江家在不考虑他人帮工等其它因素的前提下,怎样安排中籼稻和棉花的种植面积才能保证P最大?最大值是多少?
解:(1)由表(1)可得

=2515.6(元).
答:李江家从国家开始减征农业税后两年可少交农业税2515.6元.
(2)
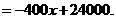
(3)由题意,可得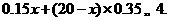
解之,得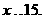
由于-400<0,所以P随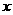 的减小而增大.
的减小而增大.
所以,当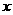 =15时,
=15时, (元).
(元).
∴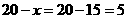 (亩).
(亩).
27、(盐城市2004)分别解不等式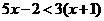 和
和 ,再根据它们的解集写出x与y的大小关系.
,再根据它们的解集写出x与y的大小关系.
.解:不等式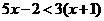 的解集为
的解集为 ;不等式
;不等式 的解集为
的解集为
 .
.
26、(2004年新疆)用若干辆载重量为8吨的汽车运一批货物,若每辆汽车只装5吨,则剩下10吨货物,若每辆车装满8吨,则最后一辆汽车不空也不满,请问有多少辆汽车?
设有x辆汽车
则
解之得:1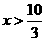 2
2 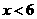
∴不等式组解集为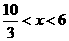 ∴满足不等式组解集的整数解为4或5
∴满足不等式组解集的整数解为4或5
25、(淄博市2004)我市一山区学校为部分家远的学生安排住宿,将部分教室改造成若干间住房. 如果每间住5人,那么有12人安排不下;如果每间住8人,那么有一间房还余一些床位,问该校可能有几间住房可以安排学生住宿?住宿的学生可能有多少人?
解:设有x间住房,有y名学生住宿.
根据题意,得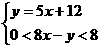 ……………………3分
……………………3分
把①代入②,得
0 8x-5x-12
8x-5x-12 8
8
解得  . ……………………………………………………… 5分
. ……………………………………………………… 5分
因为x为整数,所以x可取5,6, …………………………………………6分
把x的值代入①,得y的值为37,42. ………………………………… 7分
答:该校可能有5间或6间住房,当有5间住房时,住宿学生有37人;当有6间住房时,住宿学生有42人.
24、(镇江市2004) 修建润扬大桥,途经镇江某地,需搬迁一批农户,为了节约土地资源和保护环境,政府决定统一规划建房小区,并且投资一部分资金用于小区建设和补偿到政府规划小区建房的搬迁农户.建房小区除建房占地外,其余部分政府每平方米投资100元进行小区建设;搬迁农户在建房小区建房,每户占地100 平方米,政府每户补偿4万元,此项政策,吸引了搬迁农户到政府规划小区建房,这时建房占地面积占政府规划小区总面积的20%. 政府又鼓励非搬迁户到规划小区建房,每户建房占地120平方米,但每户需向政府交纳土地使用费2.8万元,这样又有20户非搬迁户申请加入.此项政策,政府不但可以收取土地使用费,同时还可以增加小区建房占地面积,从而减少小区建设的投资费用.若这20户非搬迁户到政府规划小区建房后,此时建房占地面积占政府规划规划小区总面积的40%. (1)设到政府规划小区建房的搬迁农户为x户,政府规划小区总面积为y平方米. 可得方程组 解得 (2)在20户非搬迁户加入建房前,请测算政府共需投资 __________万元 在20户非搬迁户加入建房后,请测算政府将收取的土地使用费投入后,还需投资
 __________万元.
(3)设非搬迁户申请加入建房并被政府批准的有z户,政府将收取的土地使用费投入
__________万元.
(3)设非搬迁户申请加入建房并被政府批准的有z户,政府将收取的土地使用费投入
后,还需投资p万元. ①求p与z的函数关系式. ②当p不高于140万元,而又使建房占地面积不超过规划小区总面积的35%时,
那么政府可以批准多少户非搬迁户加入建房?
(1)

(2)192…………………………………5分
112…………………………………6分
(3)①
 ………………………………7分
………………………………7分
②由题意得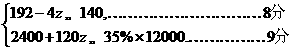
解得
∴政府可批准13、14或15户非搬迁户加入建房.
23、 (黄石市2005)已知关于x的不等式2x+m>-5的解集如图所示,则m的值为( A )
(黄石市2005)已知关于x的不等式2x+m>-5的解集如图所示,则m的值为( A )
A.1 B.0
C.-1 D.-2
22、(绵阳2005)如果关于x的不等式 (a+1) x>a+1的解集为x<1,那么a的取值范围是D
A. a>0 B. a<0 C. a>-1 D. a<-1
21、(2005南充)某钢铁企业为了适应市场竞争的需要,提高生产效率,决定将一部分钢铁生产一线员工调整去从事服务性工作.该企业现有钢铁生产一线员工1000人,平均每人全年可创造钢铁产品产值30万元.根据规划,调整出去一部分一线员工后,生产一线员工平均每人全年创造钢铁产品产值可增加30%,调整到服务性工作岗位人员平均每人全年可创造产值24万元.如果要保证员工岗位调整后,它们全年的总产值至少增加20%,并且钢铁产品的产值不能超过33150万元.怎样安排调整到服务性工作岗位的人数?
解:设从现有钢铁生产一线员工中调整x人从事服务性工作. …………(1分)
根据题意,建立不等式组:
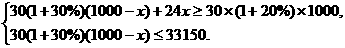 ……………(5分)
解不等式1,得x≤200.
解不等式2,得x≥150. ……………………(7分)
即不等式组的解集是 150≤x≤200.
答:安排调整到服务性工作岗位的人数不低于150人,不超过200人.
……………(5分)
解不等式1,得x≤200.
解不等式2,得x≥150. ……………………(7分)
即不等式组的解集是 150≤x≤200.
答:安排调整到服务性工作岗位的人数不低于150人,不超过200人.
20、(厦门2005) 某软件公司开发出一种图书管理软件,前期投入的开发、广告宣传费用共50000元,且每售出一套软件,软件公司还需支付安装调试费用200元.
(1)试写出总费用y(元)与销售套数x(套)之间的函数关系式;
(2)如果每套定价700元,软件公司至少要售出多少套软件才能确保不亏本?
(1) 解:y=50000+200x …… 4分
(2) 解1:设软件公司至少要售出x套软件才能确保不亏本,则有:
700 x≥50000+200x …… 7分
解得:x≥100 …… 9分
答:软件公司至少要售出100套软件才能确保不亏本. …… 10分
解2:每套成本是+200 …… 5分
若每套成本和销售价相等则:700=+200 …… 7分
解得:1= ∴ x=100 …… 9分
答:软件公司至少要售100套软件才能确保不亏本. …… 10分
解3:每套成本是+200 …… 5分
由题意得:700≥+200 …… 7分
解得:1≥ ∴ x≥100
19、(连云港市2005)光明农场现有某种植物10 000kg,打算全部用于生产高科技药品和保健食品.若生产高科技药品,1kg该植物可提炼出0.01kg的高科技药品,将产生污染物0.1kg;若生产保健食品,1kg该植物可制成0.2kg的保健食品,同时产生污染物0.04kg.已知每生产1kg高科技药品可获利润5 000元,每生产1kg保健食品可获利润100元.要使总利润不低于410 000元,所产生的污染物总量不超过880kg,求用于生产高科技药品的该植物重量的范围.
解:设用于生产高科技药品的该植物重量为xkg,则用于生产保健食品的植物重量为 kg.
根据题意,得
kg.
根据题意,得 
解得 7000≤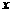 ≤8000.
≤8000.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com