
题目列表(包括答案和解析)
2.在一服装厂里有大量形状为等腰直角三角形的边角布料(如图7).现找出其中的一种,测得∠C=90°,AC=BC=4,今要从这种三角形中剪出一种扇形,做成不同形状的玩具,使扇形的边缘半径恰好都在△ABC的边上,且扇形的弧与△ABC的其它边相切.请设计出所有可能符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形半径)

1.问题:要将一块直径为2m的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面。
操作:
方案一:在图1中,设计一个圆锥底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图);
方案二:在图2中,设计一个圆柱两个底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图)。
探究:
⑴求方案一中圆锥底面的半径;
⑵求方案二中半圆圆心为O,圆柱两个底面圆心为O1、O2,圆锥底面的圆心为O3,试判断以
O1、O2、O3、O为顶点的四边形是什么样的特殊四边形,并加以证明。


45、(2004年福建三明)已知不等式组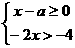 有解,则
有解,则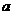 的取值范围为
的取值范围为
(A)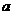 >-2 (B)
>-2 (B)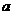 ≥-2 (C)
≥-2 (C)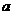 <2 (D)
<2 (D)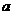 ≥2 .
答:[
C ]
≥2 .
答:[
C ]
44、(湖州市2004)织里某童装加工企业今年五月份工人每人平均加工童装150套,最不熟练的工人加工的童装套数为平均套数的60%。为了提高工人的劳动积极性,按时完成外商订货任务,企业计划从六月份起进行工资改革。改革后每位工人的工资分二部分:一部分为每人每月基本工资200元;另一部分为每加工1套童装奖励若干元。
(1)为了保证所有工人的每月工资收入不低于市有关部门规定的最低工资标准450元,按五月份工人加工的童装套数计算,工人每加工1套童装企业至少应奖励多少元(精确到分)?
(2)根据经营情况,企业决定每加工1套童装奖励5元。工人小张争取六月份工资不少于1200元,问小张在六月份应至少加工多少套童装?
解:(1)设企业每套奖励x元, 由题意得:200+60%·150x≥450
解得:x≥2.78 因此,该企业每套至少应奖励2.78元。
(2)设小张在六月份加工y套 由题意得:200+5y≥1200 解得:y≥200。
43、(2004年河北)光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.
两地区与该农机租赁公司商定的每天的租赁价格见下表:
|
|
每台甲型收割机的租金 |
每台乙型收割机的租金 |
|
A地区 |
1800元 |
1600元 |
|
B地区 |
1600元 |
1200元 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说
明有多少种分派方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提
出一条合理建议.
解:(1)若派往A地区的乙型收割机为x台,则派往A地区的甲型收割机为(30-x)台;派往B地区的乙型收割机为(30-x)台,派往B地区的甲型收割机为(x-10)台.
∴y=1600x+1800(30-x)+1200(30-x)+1600(x-10)=200x+74000.
x的取值范围是:10≤x≤30(x是正整数).
(2)由题意得200x+74000≥79600,
解不等式得x≥28.由于10≤x≤30,∴x取28,29,30这三个值,
∴有3种不同分配方案.
① 当x=28时,即派往A地区甲型收割机2台,乙型收割机28台;派往B
地区甲型收割机18台,乙型收割机2台.
② 当x=29时,即派往A地区甲型收割机1台,乙型收割机29台;派往B
地区甲型收割机19台,乙型收割机1台.
③ 当x=30时,即30台乙型收割机全部派往A地区;20台甲型收割机全部派往B地区.
(3)由于一次函数y=200x+74000的值y是随着x的增大而增大的,所以,当x=30时,y取得最大值.如果要使农机租赁公司这50台联合收割机每天获得租金最高,只需x=30,此时,y=6000+74000=80000.
建议农机租赁公司将30台乙型收割机全部派往A地区;20台甲型收割要全部派往B地区,可使公司获得的租金最高.
42、(日照市2004)已知关于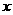 的不等式组
的不等式组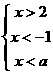 ,无解,则
,无解,则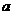 的取值范围是
( D )
的取值范围是
( D )
A 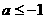 B
B 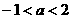 C
C  D
D 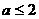
40、(淮安市2004) 国泰玩具厂工人的工作时间:每月25天,每天8小时.待遇:按件计酬,多劳多得,每月另加福利工资100元,按月结算.该厂生产A、B两种产品,工人每生产一件A种产品,可得报酬0.75元,每生产一件B种产品,可得报酬1.40元.下表记录了工人小李的工作情况:
|
生产A种产品件数(件) |
生产B种产品件数(件) |
总时间(分) |
|
l |
1 |
35 |
|
3 |
2 |
85 |
根据上表提供的信息,请回答下列问题:
(1)小李每生产一件A种产品、每生产一件B种产品,分别需要多少分钟?
(2)如果生产各种产品的数目没有限制,那么小李每月的工资数目在什么范围之内?
解:(1)解:设小李每生产一件A种产品、每生产一件B种产品分别需要x分钟和y
分钟,根据题意,得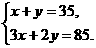 解之,得
解之,得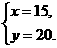
(由记录表直接推出正确结论的,同样给分)
(2)方法一:设小李每月生产A种产品x件,B种产品y件(x、y均为非负整数),月工资
数目为w元, 根据题意,得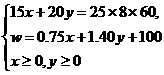 ,即
,即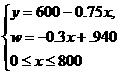
由于- 0.3<0,因此当x=O时,w最大=-O.3·0+940=940
当x=800时,w最小=-O.3·800+940=700.
因为生产各种产品的数目没有限制,所以700≤w≤940.
即小李每月的工资数目不低于700元而不高于940元.
方法二:由(1)知小李生产A种产品每分钟可获利O.05元,生产B种产品每分钟可获利O.07元, 若小李全部生产A种产品,每月的上资数目为700元,若小李全部生产B种产品,每月的工资数目为940元
小李每月的工资数目不低于700元而不高于940元.
39、(荆门2004)为了改善城乡人民生产、生活环境,我市投入大量资金,治理竹皮河污染,在城郊建立了一个综合性污水处理厂,设库池中存有待处理的污水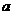 吨,又从城区流入库池的污水按每小时
吨,又从城区流入库池的污水按每小时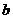 吨的固定流量增加.如果同时开动2台机组需30小时处理完污水,同时开动4台机组需10小时处理完污水.若要求5小时内将污水处理完毕,那么至少要同时开动多少台机组?
吨的固定流量增加.如果同时开动2台机组需30小时处理完污水,同时开动4台机组需10小时处理完污水.若要求5小时内将污水处理完毕,那么至少要同时开动多少台机组?
解:设1台机组每小时处理污水v吨,要在5小时内处理完污水,至少需开动x台机组,则……………………………………………………………………………………… 1分
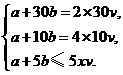 (①②各1分,③2分,其中③写成等式不扣分)… 5分
(①②各1分,③2分,其中③写成等式不扣分)… 5分
由得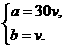 ……………………………………………………………………… 7分
……………………………………………………………………… 7分
代入得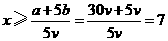 .
.
38、(荆门2004)现用甲、乙两种运输车将46吨抗旱物资运往灾区,甲种运输车载重5吨,乙种运输车载重4吨,安排车辆不超过10辆,则甲种运输车至少应安排C
A.4辆 B.5辆 C.6辆 D.7辆
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com