8．三角形三边的长分别为3，4，x，那么三角形的周长y与边长

x的函数关系式是_______，x的取值范围是_____________。

7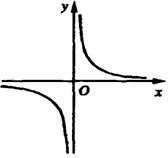．某同学解分式方程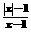=0，得出原方程的解为x=1或x=-1。你认为他的解答对吗?请你作出判断，并说明理由______________________________。

6．等腰梯形的上底长为2，下底长为4，高为1，那么下底角的正弦值是_______。

5．要做一个底面直径为acm，高为bcm的圆柱侧面模型，

要剪裁的长方形纸片的面积为__________。

4．如果|a+2|+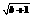=0，那么a、b的大小关系为a_____b

(填“＞”“=”或“<”)

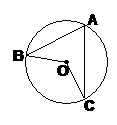
3．如图，A、B、C是⊙O上三点，∠BOC=150º，则∠A=_______。

1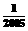．的倒数是_________。　　　　　　　 2．分解因式：ax―a=_________________。

25．(本题10分)

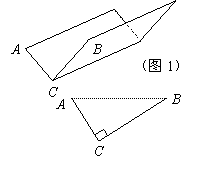
现有边长为120 cm的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．

(1)小明认为，在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．于是他对水槽的横截面设计了如下两种方案：

方案①：把它折成横截面为直角三角形的水槽(如图1)．

若∠ACB=90°，设AC=x (cm)，该水槽的横截面面积为y (cm²)，请你写出y关于x的函数关系式(不必写出x的取值范围)，并求出当x取何值时，y的值最大，最大值是多少？

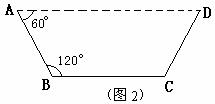
方案②：把它折成横截面为等腰梯形的水槽(如图2)．

若∠ABC=120°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小．

(2)请你再提供两种方案，使你所设计的水槽的横截面面积比小明设计的更大．画出你设计的草图，标上必要的数据(不要求写出解答过程)．

24、(本小题满分9分)

已知：在矩形ABCD中，AB=6cm，AD=9cm，点P从点B出发，沿射线BC方向以每秒2cm的速度移动，同时，点Q从点D出发，沿线段DA以每秒1cm的速度向点A方向移动(当点Q到达点A时，点P与点Q同时停止移动)，PQ交BD于点E．假设点P移动的时间为x(秒)，△BPE的面积为y(cm²)．

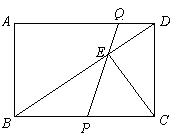(1)求证：在点P、Q的移动过程中，线段BE的长度保持不变；

(2)求y关于x的函数解析式，并写出自变量的取值范围；

(3)如果CE=CP，求x的值．

23、某医药研究所进行某一治疗病毒新药的开发，经过大量的服用试验后知：成年人按规定的剂量服用后，每毫克血液中含药量y微克(1微克=10^-3毫克)随时间x小时的变化规律与某一个二次函数y=ax²+bx+c (a≠0)相吻合，并测得服用时(即时间为0时)每毫升血液中含药量为0微克；服用后2小时每毫升血液中含药量为6微克，服用后3小时，每毫升血液中含药量为7.5微克。

(1)求出含药量y(微克)与服药时间x(小时)的函数关系式；并画出0≤x≤8内的函数的图象的示意图；

(2)求服药后几小时才能使每毫升血液中含药量最大？并求出血液中的最大含药量；

(3)结合图象说明一次服药后的有效时间是多少小时？(有效时间为血液中含药量不为0的总时间)