
题目列表(包括答案和解析)
3.在△ABC和△DEF中,已知∠C=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件
(A)AB=ED (B)AB=FD (C)AC=FD (D)∠A=∠F
2.不等式组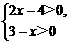 的解集为
的解集为
(A)2<x<3 (B)x>3 (C)x<2 (D)x>2或 x<-3
1.下列计算结果正确的是
(A)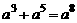 (B)
(B)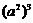 =
=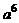
(C)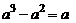 (D)
(D)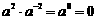
26. (本题满分13分) 已知:O是坐标原点,P(m,n)(m>0)是函数y = (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m). 设△OPA的面积为s,且s=1+.
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值;
(3 ) 设n是小于20的整数,且k≠,求OP2的最小值.
厦门市2005年初中毕业和高中阶段各类学校招生考试
25. (本题满分12分) 已知:⊙O1与⊙O2相交于点A、B,过点B作CD⊥AB,分别交⊙O1和⊙O2于点C、D.
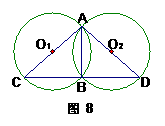
(1)如图8,求证:AC是⊙O1的直径;
(2)若AC=AD,
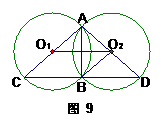
① 如图9,连结BO2、O1 O2,求证:四边形O1C BO2是平行四边形;
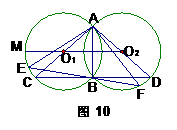
② 若点O1在⊙O2外,延长O2O1交⊙O1于点M,在劣弧︵MB上任取一点E(点E与点B不重合). EB的延长线交优弧︵BDA于点F,如图10所示. 连结 AE、AF. 则AE AB(请在横线上填上 “≥、≤、<、>”这四个不等号中的一个)并加以证明.
(友情提示:结论要填在答题卡相应的位置上)
24. (本题满分12分) 已知抛物线y=x2-2x+m与x轴交于点A(x1,0)、B(x2,0)(x2>x1),
(1) 若点P(-1,2)在抛物线y=x2-2x+m上,求m的值;
(2)若抛物线y=ax2+bx+m与抛物线y=x2-2x+m关于y轴对称,点Q1(-2,q1)、Q2(-3,q2)都在抛物线y=ax2+bx+m上,则q1、q2的大小关系是
(请将结论写在横线上,不要写解答过程);
(友情提示:结论要填在答题卡相应的位置上)
(3)设抛物线y=x2-2x+m的顶点为M,若△AMB是直角三角形,求m的值.
23. (本题满分10分) 已知:如图7,P是正方形ABCD
内一点,在正方形ABCD外有一点E,
满足∠ABE=∠CBP,BE=BP,
(1) 求证:△CPB≌△AEB;
(2) 求证:PB⊥BE;
(3) 若PA∶PB=1∶2,∠APB=135°,
求cos∠PAE的值.
22. (本题满分10分) 某软件公司开发出一种图书管理软件,前期投入的开发、广告宣传费用共50000元,且每售出一套软件,软件公司还需支付安装调试费用200元.
(1)试写出总费用y(元)与销售套数x(套)之间的函数关系式;
(2)如果每套定价700元,软件公司至少要售出多少套软件才能确保不亏本?

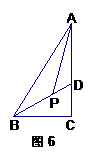
21. (本题满分10分) 如图6,已知:在直角△ABC中,∠C=90°,
BD平分∠ABC且交AC于D.
(1)若∠BAC=30°,求证: AD=BD;
(2)若AP平分∠BAC且交BD于P,求∠BPA的度数.
20. (本题满分8分) 某市举行一次少年滑冰比赛,各年龄组的参赛人数如下表所示:
|
年龄组 |
13岁 |
14岁 |
15岁 |
16岁 |
|
参赛人数 |
5 |
19 |
12 |
14 |
(1) 求全体参赛选手年龄的众数、中位数;
(2) 小明说,他所在年龄组的参赛人数占全体参赛人数的28%.
你认为小明是哪个年龄组的选手?请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com