8．(2004年苏州)如图，苏州某公园入口处原有三阶台阶，每级台阶高为20cm,深为30cm.为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现将斜坡的坡角∠BCA设计为12°，求AC的长度。 (精确到1 cm)

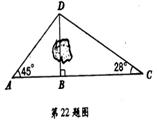
7.(2004年本溪)已知：如图，A、B、C三个村庄在一条东西走向的公路沿线上，AB=2km。在B村的正北方向有一个D村，测得∠DAB=45°，∠DCB=28°。今将△ACD区域进行规划，除其中面积为0.5 km²的水塘外，准备把剩余的一半作为绿化用地，试求绿化用地的面积。(结果精确到0.1 km²)

6.(2004年大连)如图5，某校自行车棚的人字架棚顶为等腰三角形，D是AB的中点，中柱CD = 1米，

∠A=27°，求跨度AB的长(精确到0.01米)。

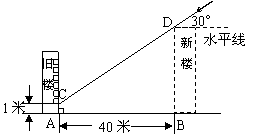
5.(2004年宁安)为解决楼房之间的挡光问题，某地区规定：两幢楼房间的距离至少为40米，中午12时不能挡光.如图，某旧楼的一楼窗台高1米，要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射，并且光线与水平线的夹角最小为30°，在不违反规定的情况下，请问新建楼房最高多少米？(结果精确到1米.)

4.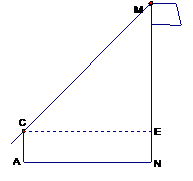(2004年青岛)在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下的方案(如图1所示)：

(1)　　　　 在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE＝α ；

(2)　　　　 量出测点A到旗杆底部N的水平距离AN＝m;

(3)　　　　 量出测倾器的高度AC＝h。

根据上述测量数据，即可求出旗杆的高度MN。

如果测量工具不变，请仿照上述过程，设计一个测量

某小山高度(如图2)的方案：

1)　 在图2中，画出你测量小山高度MN的示意图

(标上适当的字母)

2)写出你的设计方案。

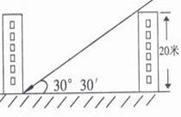
3.(2004年青岛)青岛位于北纬36°4′，在冬至日正午时分的太阳入射角为30°30，因此，在规划建设楼高为20米的小区时，两楼间的最小距离为　　 米才能够保证不挡光。(结果保留4 个有效数字，)

2.(2004年开福)在湖的两岸A、B间建一座观赏桥，由于条件限制，无法直接度量A、B两点间的距离。请你用学过的数学知识按以下要求设计一测量方案。(1)画出测量图案；(2)写出测量步骤(测量数据用字母表示)；(3)计算AB的距离(写出求解或推理过程，结果用字母表示)。

3.教具：三角板，小黑板(投影仪)圆规。

教学步骤

中考题型链接　

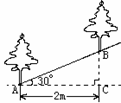
1.(2004年开福)如图，沿倾斜角为30°的山坡植树，要求相邻俩棵树的水平距离AC为2cm，那么相邻两棵树的斜坡距离AB约为　　　 m。(精确到0.1m)。

1.教法：引导复习法，指导归纳总结法，综合练习法。

2．难点：培养学生把实际问题转化为数学问题及建立数学模型的综合解题能力。

教法、学法、和教具