3.如图，弦AC，BD相交于E，且AB，BC，CD的弧长相等，∠AED＝30°，则∠AED的度数是(　　　 )

(A)150°　 (B) 105°　　 (C) 120° 　(D) 140°

2．一个点到圆的最大距离为11cm，最小距离为5cm,则圆的半径为(　　　 )

(A)16cm或6cm,　 (B)3cm或8cm 　 (C)3cm 　　(D)8cm

1．在⊿ABC中，∠C=90°，AB＝3cm，BC＝2cm,以点A为圆心，以2.5cm为半径作圆，则点C和⊙A的位置关系是(　　 )(A)C在⊙A 上　 (B)C在⊙A 外　 (C)C在⊙A 内　　 (D)C在⊙A 位置不能确定。

5.反证法的步骤。

4．注意：(1)垂径定理及其推论是指：一条弦①在“过圆心”②“垂直于另一条弦”③“平分这另一条弦”④“平分这另一条弦所对的劣弧”⑤“ 平分这另一条弦所对的优弧”的五个条件中任意具有两个条件，则必具有另外三个结论(当①③为条件时要对另一条弦增加它不是直径的限制)，条理性的记忆，不但简化了对它实际代表的10条定理的记忆且便于解题时的灵活应用，垂径定理提供了证明线段相等、角相等、垂直关系等的重要依据；(2)有弦可作弦心距组成垂径定理图形；见到直径要想到它所对的圆周角是直角，想垂径定理；想到过它的端点若有切线，则与它垂直，反之，若有垂线则是切线，想到它被圆心所平分；(3)见到四个点在圆上想到有4组相等的同弧所对的圆周角，要想到应用圆内接四边形的性质。(4)等弧的概念等。

3．圆的有关性质：同(等)圆中半径相等、直径相等；直径是半径的2倍；直径是最大的弦；圆是轴对称图形，经过圆心的任一条直线都是对称轴；圆是中心对称图形，圆心是对称中心；圆具有旋转不变性；垂径定理及其推论；圆心角、圆周角、弧、弦、弦心距之间的关系；圆心角、圆周角与所对的弧的度数关系；圆内接四边形的性质定理。

2．确定一个圆的条件，即圆心、半径(直径)；不在同一直线上三点。一个圆的圆心只确定圆的位置，而半径也只能确定圆的大小，两个条件确定一条直线，三个条件确定一个圆，过三角形的三个顶点的圆存在并且唯一。

1．圆的点集定义及点和圆的位置关系

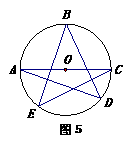
15．(2004年河南)如图5，已知A、B、C、D、E均在⊙O上，且AC为

⊙O的直径，则∠A+∠B+∠C=_____________度.

14.(2004年杭州)直线AB交圆于A，B，点M在圆上，点P在圆外，且点M，P在AB的同侧，∠AMB=50º。设∠APB=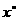，当点P移动时，求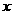的变化范围，并说明理由。