
题目列表(包括答案和解析)
2.O是⊿ABC的内心,∠BOC为130°,则∠A的度数为( )(A)130°(B)60°(C)70°(D)80°
1.如图⊙O切AC于B,AB=OB=3,BC=,∠AOC的度数(A)90 °(B)105°(C)75°(D)60°
5.注意:(1)当已知圆的切线时,切点的位置一般是确定的,在写条件时应说明直线和圆相切于哪一点,辅助线是作出过定点的半径;当证明直线是圆的切线时,如果已知直线过圆上某一点则可作出这一点的半径证明直线垂直于该半径;即为“连半径证垂直得切线”;若已知条件中未明确给出直线和圆有公共点时,则应过圆心作直线的垂线,证明圆心到直线的距离等于半径,即为:“作垂直证半径得切线”。(2) 见到切线要想到它垂直于过切点的半径;若过切点有垂线则必过圆心;过切点有弦,则想到弦切角定理,想到圆心角、圆周角性质,可再联想同圆或等圆弧弦弦心距等的性质应用。(3)任意三角形有且只有一个内切圆,圆心为这个三角形内角平分线的交点。
3.圆的切线性质和综合运用切线判定定理和性质定理解决有关问题:(1)切线与圆只有一个公共点;(2)圆心到切线距离等于半径;(3)圆的切线垂直于过切点的半径;(4) 经过圆心且垂直于切线的直线必过切点;(5)经过切点且垂直于切线的直线必过圆心;(6)切线长定理;(7) 弦切角定理及其推论。
4,掌握三角形外切圆及圆外切四边形的性质及应用;
2.直线和圆相切的三种判定方法和应用:(1)直线和圆有唯一公共点;(2)d=R;(3)切线的判定定理 (应用判定定理是满足一是过半径外端,二是与这半径垂直的二个条件才可判定是圆的切线)
1. 直线和圆的位置关系的性质和判定;
直线和圆的位置关系的性质和判定;
8.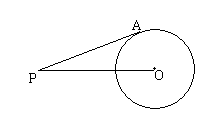 如图,PA切⊙O于点A,若
如图,PA切⊙O于点A,若 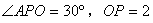 ,则⊙O的半径是( )
,则⊙O的半径是( )
A. 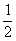 B.
B. 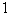 C.
C. 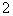 D.
D.
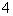
7.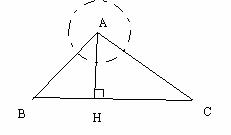 ( 2004年重庆)如图,点A是一个半径为300米的圆形森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000米的笔直公路将两村连通。经测得∠ABC=45°,∠ACB=30°,问此公路是否会穿过该森林公园?请通过计算进行说明。
( 2004年重庆)如图,点A是一个半径为300米的圆形森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000米的笔直公路将两村连通。经测得∠ABC=45°,∠ACB=30°,问此公路是否会穿过该森林公园?请通过计算进行说明。
6.( 2004年北碚)如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC的大小是 ( )
A、70° B、40° C、50° D、20°
5.( 2004年潍坊)Rt△ABC中,∠C=90°,AC=3cm,BC=4cm.给出下列三个结论:
①以点C为圆心,2.3cm长为半径的圆与AB相离;
②以点C为圆心,2.4cm长为半径的圆与AB相切;
③以点C为圆心,2.5cm长为半径的圆与AB相交;
 则上述结论中正确的个数是 A.0个 B.1个 C.2个 D.3个
则上述结论中正确的个数是 A.0个 B.1个 C.2个 D.3个
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com