
题目列表(包括答案和解析)
9、已知两圆的半径分别为6 和8
和8 ,圆心距为2
,圆心距为2 ,那么这两圆的公切线有( )
,那么这两圆的公切线有( )
A. 1条 B. 2条 C. 3条 D. 4条
|
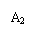
|
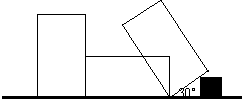

 其中第二次翻滚时被桌面上一小木块挡住,使
其中第二次翻滚时被桌面上一小木块挡住,使
|
走过的路径长为( )
A. 10cm B. 4π cm C. 3.5π cm D. 2.5πcm
8、已知小明同学身高1.5 ,经太阳光照射,在地面的影长为2
,经太阳光照射,在地面的影长为2 ,若此时测得一塔在同一地面的影长为60
,若此时测得一塔在同一地面的影长为60 ,则塔高应为(
)
,则塔高应为(
)
A. 40 B. 45
B. 45 C. 80
C. 80 D. 90
D. 90
7、设有12只型号相同的杯子,其中一等品7只,二等品3只,三等品2只,则从中任取1只,是二等品的概率等于( )
A.
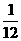 B.
B. 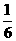 C.
C. 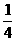 D.
D. 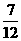
6、下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是( )

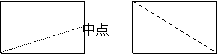
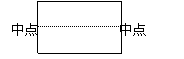
A B C D
5、过点(2,3)的正比例函数解析式是( )
A.
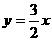 B.
B. 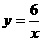 C.
C. 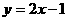 D.
D. 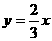
4、已知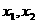 是方程
是方程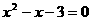 的两根,那么
的两根,那么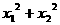 的值是(
)
的值是(
)
A.
1
B. 5
C. 7
D. 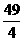
3、计算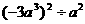 的结果是(
)
的结果是(
)
A. 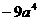 B.
B. 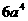 C.
C. 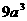 D.
D. 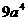
2、世界文化遗产长城的总长为6700000m,用科学记数法可表示为( )
A. 6.7×105 B. 6.7×10-5 C. 6.7×106 D. 6.7×10-6
1、在1,–1,–2这三个数中,任意两数之和的最大值是( )
A. 1 B. 0 C. –1 D. –3
25、(本题14分)在如图所示的平面直角坐标系中,定圆圆心A(0.3),⊙A与x轴相切, ⊙B的圆心在X轴的正半轴上移动.
(1)当⊙B半径为2,且两圆外切时,求B点坐标.
(2)在(1)的条件下,记⊙B与⊙A外切于点P,两圆的公切线MP交Y轴于点M,交X轴于点N,求直线MP的解析式及经过M、N、B三点的抛物线的解析式。
(3)若⊙B的圆心在X轴的正半轴上移动,始终保持⊙B与⊙A外切,设⊙B半径为r,B(x,0),求r与x的函数解析式。
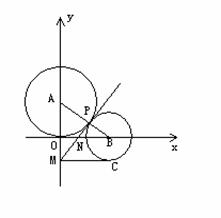 (4)在(3)的条件下,过M作⊙B的切线MC,切点为C,①探究四边形OMCB是什么四边形,对你的结论加以证明。②经过M、N、B三点的抛物线内是否存在以BN为腰的等腰三角形?若存在,表示出来;若不存在,说明理由。
(4)在(3)的条件下,过M作⊙B的切线MC,切点为C,①探究四边形OMCB是什么四边形,对你的结论加以证明。②经过M、N、B三点的抛物线内是否存在以BN为腰的等腰三角形?若存在,表示出来;若不存在,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com