
题目列表(包括答案和解析)
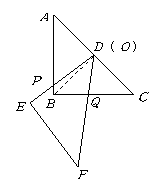
9、(2006湖南常德)把两块全等的直角三角形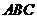 和
和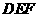 叠放在一起,使三角板
叠放在一起,使三角板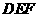 的锐角顶点
的锐角顶点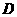 与三角板
与三角板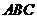 的斜边中点
的斜边中点 重合,其中
重合,其中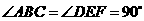 ,
,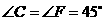 ,
,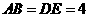 ,把三角板
,把三角板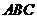 固定不动,让三角板
固定不动,让三角板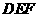 绕点
绕点 旋转,设射线
旋转,设射线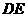 与射线
与射线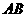 相交于点
相交于点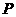 ,射线
,射线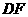 与线段
与线段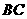 相交于点
相交于点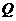 .
.
(1)如图9,当射线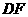 经过点
经过点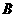 ,即点
,即点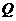 与点
与点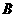 重合时,易证
重合时,易证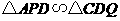 .此时,
.此时, .
.
(2)将三角板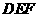 由图1所示的位置绕点
由图1所示的位置绕点 沿逆时针方向旋转,设旋转角为
沿逆时针方向旋转,设旋转角为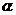 .其中
.其中
 ,问
,问 的值是否改变?说明你的理由.
的值是否改变?说明你的理由.
 (3)在(2)的条件下,设
(3)在(2)的条件下,设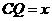 ,两块三角板重叠面积为
,两块三角板重叠面积为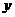 ,求
,求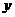 与
与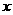 的函数关系式.
的函数关系式.
[解] (1)8
 (2)
(2) 的值不会改变.
的值不会改变.
理由如下:在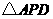 与
与 中,
中,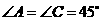


即
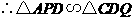
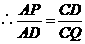
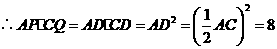
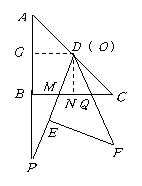 (3)情形1:当
(3)情形1:当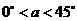 时,
时, ,即
,即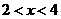 ,此时两三角板重叠部分为四边形
,此时两三角板重叠部分为四边形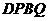 ,过
,过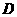 作
作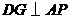 于
于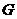 ,
, 于
于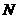 ,
,
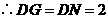
由(2)知: 得
得
于是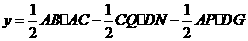

情形2:当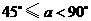 时,
时,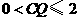 时,即
时,即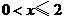 ,此时两三角板重叠部分为
,此时两三角板重叠部分为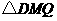 ,
,
由于 ,
,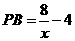 ,易证:
,易证: ,
,
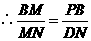 即
即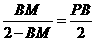 解得
解得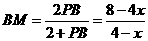
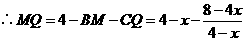
于是
综上所述,当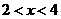 时,
时,
当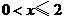 时,
时,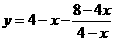

法二:连结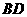 ,并过
,并过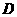 作
作 于点
于点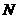 ,在
,在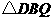 与
与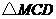 中,
中,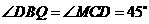
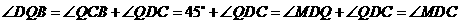
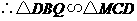
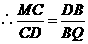
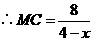
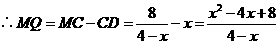
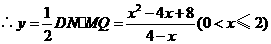
法三:过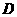 作
作 于点
于点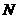 ,在
,在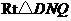 中,
中,
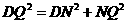
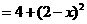
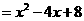
于是在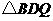 与
与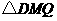 中
中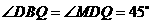
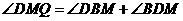
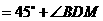
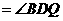
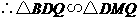
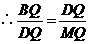
即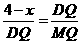
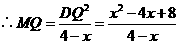
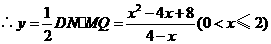
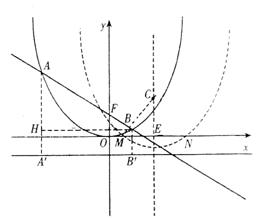
8、(2006吉林长春)如图,在平面直角坐标系中,两个函数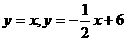 的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S。
的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S。
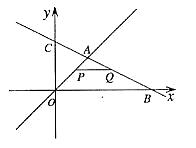 (1)求点A的坐标。
(1)求点A的坐标。
(2)试求出点P在线段OA上运动时,S与运动时间t(秒)的关系式。
(3)在(2)的条件下,S是否有最大值?若有,求出t为何值时,S有最大值,并求出最大值;若没有,请说明理由。
(4)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积最大时,运动时间t满足的条件是____________。
[解] (1)由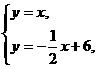 可得
可得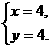
∴A(4,4)。
(2)点P在y = x上,OP = t,
则点P坐标为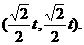
点Q的纵坐标为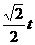 ,并且点Q在
,并且点Q在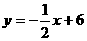 上。
上。
∴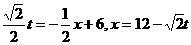 ,
,
即点Q坐标为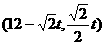 。
。
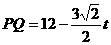 。
。
当 时,
时,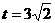 。
。
当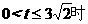 ,
,
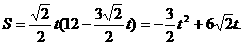
当点P到达A点时,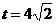 ,
,
当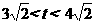 时,
时,
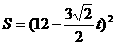
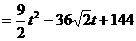 。
。
(3)有最大值,最大值应在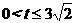 中,
中,
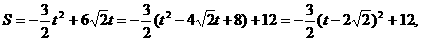
当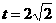 时,S的最大值为12。
时,S的最大值为12。
(4)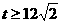 。
。
7、(2006江西)问题背景 某课外学习小组在一次学习研讨中,得到了如下两个命题:
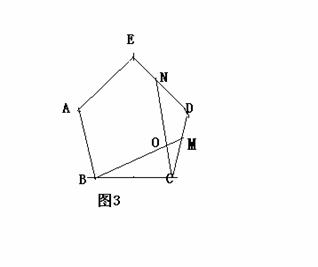
①如图1,在正三角形△ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60º,则BM=CN;
②如图2,在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90º,则BM=CN;
然后运用类比的思想提出了如下命题:
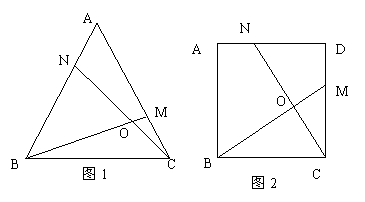
③如图3,在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON=108º,则BM=CN。
任务要求:
(1)请你从①、②、③三个命题中选择一个进行证明;(说明:选①做对得4分,选②做对得3分,选③做对得5分)
(2)请你继续完成下列探索:
①请在图3中画出一条与CN相等的线段DH,使点H在正五边形的边上,且与CN相交所成的一个角是108º,这样的线段有几条?(不必写出画法,不要求证明)
②如图4,在正五边形ABCDE中,M、N分别是DE、EA上的点,BM与CN相交于点O,若∠BON=108º,请问结论BM=CN是否还成立?若成立,请给予证明;若不成立,请说明理由。
[解] (1)以下答案供参考:
(1) 如选命题①
证明:在图1中,∵∠BON=60°∴∠1+∠2=60°
∵∠3+∠2=60°,∴∠1=∠3
又∵BC=CA,∠BCM=∠CAN=60°∴ΔBCM≌ΔCAN
∴BM=CN (2)如选命题②
证明:在图2中,∵∵∠BON=90°∴∠1+∠2=90°
∵∠3+∠2=90°,∴∠1=∠3
又∵BC=CD,∠BCM=∠CDN=90°∴ΔBCM≌ΔCDN
∴BM=CN
(3)如选命题③
证明;在图3中,∵∠BON=108°∴∠1+∠2=108°
∵∠2+∠3=108°∴∠1=∠3
又∵BC=CD,∠BCM=∠CDN=108°
∴ΔBCM≌ΔCDN
∴BM=CN
(2)①答:当∠BON= 时结论BM=CN成立.
时结论BM=CN成立.
②答当∠BON=108°时。BM=CN还成立
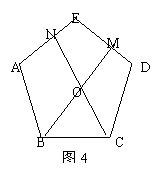
证明;如图5连结BD、CE.
在△BCI)和△CDE中
∵BC=CD, ∠BCD=∠CDE=108°,CD=DE
∴ΔBCD≌ ΔCDE
∴BD=CE , ∠BDC=∠CED, ∠DBC=∠CEN
∵∠CDE=∠DEC=108°, ∴∠BDM=∠CEN
∵∠OBC+∠ECD=108°, ∠OCB+∠OCD=108°
∴∠MBC=∠NCD
又∵∠DBC=∠ECD=36°, ∴∠DBM=∠ECN
∴ΔBDM≌ ΔCNE ∴BM=CN
6、(2006山东潍坊)已知二次函数图象的顶点在原点 ,对称轴为
,对称轴为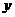 轴.一次函数
轴.一次函数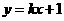 的图象与二次函数的图象交于
的图象与二次函数的图象交于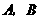 两点(
两点( 在
在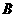 的左侧),且
的左侧),且 点坐标为
点坐标为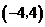 .平行于
.平行于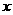 轴的直线
轴的直线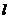 过
过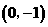 点.
点.
(1)求一次函数与二次函数的解析式;
(2)判断以线段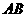 为直径的圆与直线
为直径的圆与直线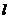 的位置关系,并给出证明;
的位置关系,并给出证明;
 (3)把二次函数的图象向右平移
(3)把二次函数的图象向右平移 个单位,再向下平移
个单位,再向下平移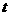 个单位
个单位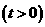 ,二次函数的图象与
,二次函数的图象与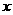 轴交于
轴交于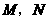 两点,一次函数图象交
两点,一次函数图象交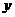 轴于
轴于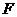 点.当
点.当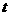 为何值时,过
为何值时,过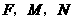 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少?
[解](1)把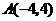 代入
代入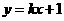 得
得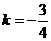 ,
,
 一次函数的解析式为
一次函数的解析式为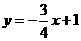 ;
;
 二次函数图象的顶点在原点,对称轴为
二次函数图象的顶点在原点,对称轴为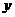 轴,
轴,
 设二次函数解析式为
设二次函数解析式为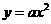 ,
,
 ·········································································· 把
·········································································· 把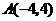 代入
代入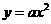 得
得 ,
,
 二次函数解析式为
二次函数解析式为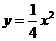 .
. 
(2)由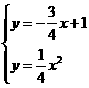
解得 或
或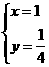 ,
,
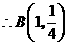 ,
,
过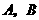 点分别作直线
点分别作直线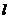 的垂线,垂足为
的垂线,垂足为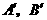 ,
,
则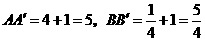 ,
,
 直角梯形
直角梯形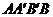 的中位线长为
的中位线长为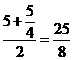 ,
,
过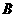 作
作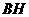 垂直于直线
垂直于直线 于点
于点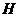 ,则
,则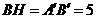 ,
,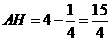 ,
,
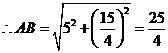 ,
,

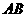 的长等于
的长等于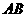 中点到直线
中点到直线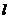 的距离的2倍,
的距离的2倍,
 以
以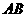 为直径的圆与直线
为直径的圆与直线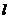 相切.
相切.
(3)平移后二次函数解析式为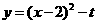 ,
,
令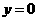 ,得
,得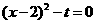 ,
, ,
,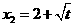 ,
,
 过
过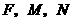 三点的圆的圆心一定在直线
三点的圆的圆心一定在直线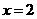 上,点
上,点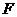 为定点,
为定点,
 ··································
··································  要使圆面积最小,圆半径应等于点
要使圆面积最小,圆半径应等于点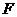 到直线
到直线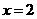 的距离,
的距离,
此时,半径为2,面积为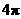 ,
,
设圆心为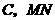 中点为
中点为 ,连
,连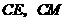 ,则
,则 ,
,
在三角形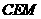 中,
中,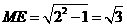 ,
,
 ,而
,而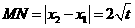 ,
,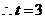 ,
,
 当
当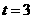 时,过
时,过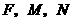 三点的圆面积最小,最小面积为
三点的圆面积最小,最小面积为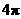 .
.
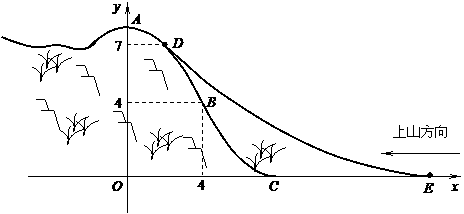
5、(2006浙江嘉兴)某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为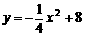 ,BC所在抛物线的解析式为
,BC所在抛物线的解析式为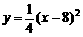 ,且已知
,且已知 .
.
(1)设 是山坡线AB上任意一点,用y表示x,并求点B的坐标;
是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).
①分别求出前三级台阶的长度(精确到厘米);
②这种台阶不能一直铺到山脚,为什么?
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,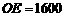 (米).假设索道DE可近似地看成一
(米).假设索道DE可近似地看成一
段以E为顶点、开口向上的抛物线,解析式为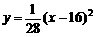 .试求索道的最大悬空高度.
.试求索道的最大悬空高度.

[解] (1)∵ 是山坡线AB上任意一点,
是山坡线AB上任意一点,
∴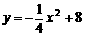 ,
,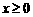 ,
,
∴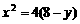 ,
,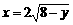
∵ ,∴
,∴ =4,∴
=4,∴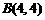
(2)在山坡线AB上,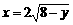 ,
,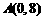
①令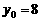 ,得
,得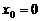 ;令
;令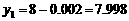 ,得
,得
∴第一级台阶的长度为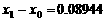 (百米)
(百米)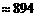 (厘米)
(厘米)
同理,令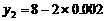 、
、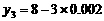 ,可得
,可得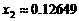 、
、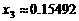
∴第二级台阶的长度为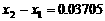 (百米)
(百米)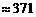 (厘米)
(厘米)
第三级台阶的长度为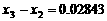 (百米)
(百米)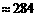 (厘米)
(厘米)
②取点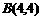 ,又取
,又取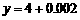 ,则
,则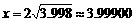
∵
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚
(注:事实上这种台阶从山顶开始最多只能铺到700米高度,共500级.从100米高度到700米高度都不能铺设这种台阶.解题时取点具有开放性)
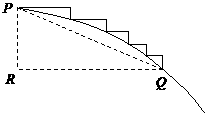 ②另解:连接任意一段台阶的两端点P、Q,如图
②另解:连接任意一段台阶的两端点P、Q,如图
∵这种台阶的长度不小于它的高度
∴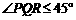
当其中有一级台阶的长大于它的高时,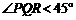
在题设图中,作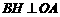 于H
于H
则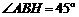 ,又第一级台阶的长大于它的高
,又第一级台阶的长大于它的高
∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚
 (3)
(3)
 、
、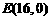 、
、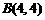 、
、
由图可知,只有当索道在BC上方时,索道的悬空高度才有可能取最大值
索道在BC上方时,悬空高度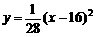
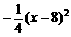
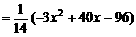
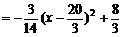
当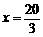 时,
时,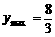
∴索道的最大悬空高度为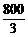 米.
米.
4、(2006山东烟台)如图,已知抛物线L1: y=x2-4的图像与x有交于A、C两点,
(1)若抛物线l2与l1关于x轴对称,求l2的解析式;
(2)若点B是抛物线l1上的一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点定为D,求证:点D在l2上;
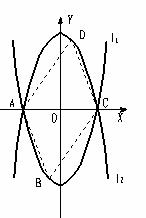 (3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。
(3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。
[解]
(1)设l2的解析式为y=a(x-h)2+k
∵l2与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),l1与l2关于x轴对称,
∴l2过A(-2,0),C(2,0),顶点坐标是(0,4)
∴y=ax2+4
∴0=4a+4 得 a=-1
∴l2的解析式为y=-x2+4
(2)设B(x1 ,y1)
∵点B在l1上
∴B(x1 ,x12-4)
∵四边形ABCD是平行四边形,A、C关于O对称
∴B、D关于O对称
∴D(-x1 ,-x12+4).
将D(-x1 ,-x12+4)的坐标代入l2:y=-x2+4
∴左边=右边
∴点D在l2上.
(3)设平行四边形ABCD的面积为S,则
S=2*S△ABC =AC*|y1|=4|y1|
a.当点B在x轴上方时,y1>0
∴S=4y1 ,它是关于y1的正比例函数且S随y1的增大而增大,
∴S既无最大值也无最小值
b.当点B在x轴下方时,-4≤y1<0
∴S=-4y1 ,它是关于y1的正比例函数且S随y1的增大而减小,
∴当y1 =-4时,S由最大值16,但他没有最小值
此时B(0,-4)在y轴上,它的对称点D也在y轴上.
∴AC⊥BD
∴平行四边形ABCD是菱形
此时S最大=16.
3、(2006山东济南)如图1,已知 中,
中,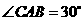 ,
,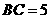 .过点
.过点 作
作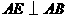 ,且
,且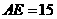 ,连接
,连接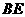 交
交 于点
于点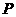 .
.
(1)求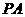 的长;
的长;
(2)以点 为圆心,
为圆心, 为半径作⊙A,试判断
为半径作⊙A,试判断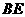 与⊙A是否相切,并说明理由;
与⊙A是否相切,并说明理由;
(3)如图2,过点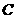 作
作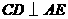 ,垂足为
,垂足为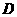 .以点
.以点 为圆心,
为圆心, 为半径作⊙A;以点
为半径作⊙A;以点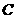 为圆心,
为圆心,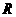 为半径作⊙C.若
为半径作⊙C.若 和
和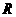 的大小是可变化的,并且在变化过程中保持⊙A和⊙C相切,且使
的大小是可变化的,并且在变化过程中保持⊙A和⊙C相切,且使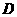 点在⊙A的内部,
点在⊙A的内部,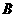 点在⊙A的外部,求
点在⊙A的外部,求 和
和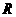 的变化范围.
的变化范围.

[解]
(1) 在
在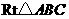 中,
中,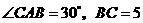 ,
,
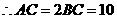 .
.
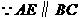 ,
,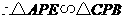 .
.
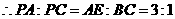 .
.
 ,
,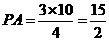 .
.
(2)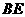 与⊙A相切.
与⊙A相切.
 在
在 中,
中,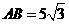 ,
,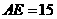 ,
,
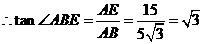 ,
, .
.
又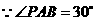 ,
,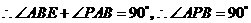 ,
,
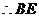 与⊙A相切.
与⊙A相切.
(3)因为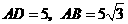 ,所以
,所以 的变化范围为
的变化范围为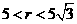 .
.
当⊙A与⊙C外切时,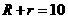 ,所以
,所以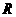 的变化范围为
的变化范围为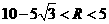 ;
;
当⊙A与⊙C内切时,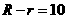 ,所以
,所以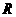 的变化范围为
的变化范围为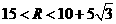 .
.
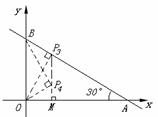
2、(2006浙江金华)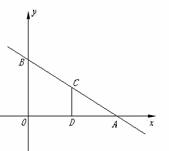 如图,平面直角坐标系中,直线AB与
如图,平面直角坐标系中,直线AB与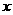 轴,
轴,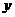 轴分别交于A(3,0),B(0,
轴分别交于A(3,0),B(0,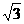 )两点, ,点C为线段AB上的一动点,过点C作CD⊥
)两点, ,点C为线段AB上的一动点,过点C作CD⊥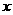 轴于点D.
轴于点D.
(1)求直线AB的解析式;
(2)若S梯形OBCD=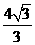 ,求点C的坐标;
,求点C的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的
三角形与△OBA相似.若存在,请求出所有符合条件
的点P的坐标;若不存在,请说明理由.
[解] (1)直线AB解析式为:y= x+
x+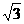 .
.
(2)方法一:设点C坐标为(x, x+
x+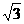 ),那么OD=x,CD=
),那么OD=x,CD= x+
x+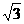 .
.
∴ =
=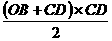 =
=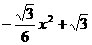 .
.
由题意: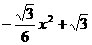 =
=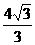 ,解得
,解得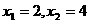 (舍去)
(舍去)
∴ C(2,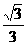 )
)
方法二:∵ 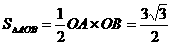 ,
, =
=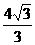 ,∴
,∴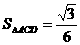 .
.
由OA=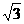 OB,得∠BAO=30°,AD=
OB,得∠BAO=30°,AD=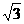 CD.
CD.
∴  =
=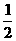 CD×AD=
CD×AD=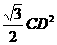 =
=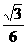 .可得CD=
.可得CD=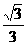 .
.
 ∴ AD=1,OD=2.∴C(2,
∴ AD=1,OD=2.∴C(2,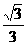 ).
).
(3)当∠OBP=Rt∠时,如图
①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP=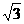 OB=3,
OB=3,
∴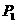 (3,
(3,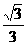 ).
).
②若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=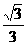 OB=1.
OB=1.
∴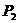 (1,
(1,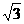 ).
).
当∠OPB=Rt∠时
③ 过点P作OP⊥BC于点P(如图),此时△PBO∽△OBA,∠BOP=∠BAO=30°
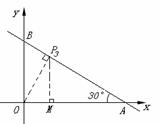 过点P作PM⊥OA于点M.
过点P作PM⊥OA于点M.
方法一: 在Rt△PBO中,BP=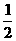 OB=
OB=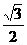 ,OP=
,OP=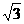 BP=
BP= .
.
∵ 在Rt△PMO中,∠OPM=30°,
∴ OM=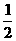 OP=
OP= ;PM=
;PM=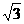 OM=
OM=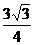 .∴
.∴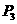 (
( ,
,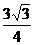 ).
).
 方法二:设P(x ,
方法二:设P(x , x+
x+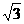 ),得OM=x ,PM=
),得OM=x ,PM= x+
x+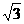
由∠BOP=∠BAO,得∠POM=∠ABO.
∵tan∠POM==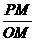 =
=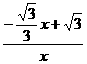 ,tan∠ABOC=
,tan∠ABOC=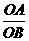 =
=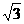 .
.
∴ x+
x+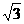 =
=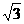 x,解得x=
x,解得x= .此时,
.此时,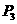 (
( ,
,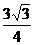 ).
).
④若△POB∽△OBA(如图),则∠OBP=∠BAO=30°,∠POM=30°.
∴ PM=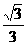 OM=
OM= .
.
∴ 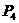 (
( ,
, )(由对称性也可得到点
)(由对称性也可得到点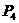 的坐标).
的坐标).
当∠OPB=Rt∠时,点P在x轴上,不符合要求.
综合得,符合条件的点有四个,分别是:
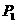 (3,
(3,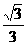 ),
),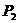 (1,
(1,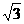 ),
),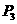 (
( ,
,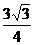 ),
),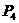 (
( ,
, ).
).
1、(2006重庆)如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成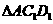 和
和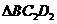 两个三角形(如图2所示).将纸片
两个三角形(如图2所示).将纸片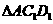 沿直线
沿直线 (AB)方向平移(点
(AB)方向平移(点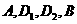 始终在同一直线上),当点
始终在同一直线上),当点 于点B重合时,停止平移.在平移过程中,
于点B重合时,停止平移.在平移过程中,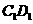 与
与 交于点E,
交于点E, 与
与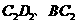 分别交于点F、P.
分别交于点F、P.
(1) 当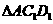 平移到如图3所示的位置时,猜想图中的
平移到如图3所示的位置时,猜想图中的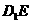 与
与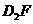 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
(2)
设平移距离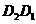 为
为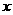 ,
,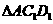 与
与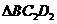 重叠部分面积为
重叠部分面积为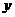 ,请写出
,请写出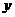 与
与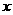 的函数关系式,以及自变量的取值范围;
的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的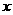 的值,使重叠部分的面积等于原
的值,使重叠部分的面积等于原 面积的
面积的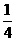 .
.
若存在,求x的值;若不存在,请说明理由.

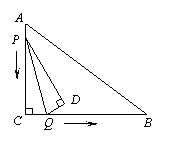 [解] (1)
[解] (1)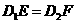 .因为
.因为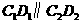 ,所以
,所以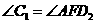 .
.
又因为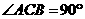 ,CD是斜边上的中线,
,CD是斜边上的中线,
所以,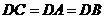 ,即
,即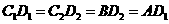
所以,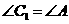 ,所以
,所以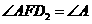
所以,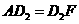 .同理:
.同理: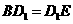 .
.
又因为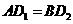 ,所以
,所以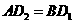 .所以
.所以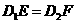
(2)因为在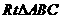 中,
中,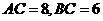 ,所以由勾股定理,得
,所以由勾股定理,得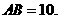
即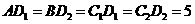
又因为 ,所以
,所以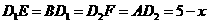 .所以
.所以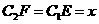
在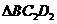 中,
中,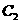 到
到 的距离就是
的距离就是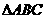 的
的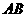 边上的高,为
边上的高,为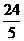 .
.
设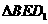 的
的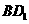 边上的高为
边上的高为 ,由探究,得
,由探究,得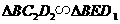 ,所以
,所以 .
.
所以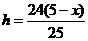 .
.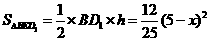
又因为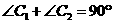 ,所以
,所以 .
.
又因为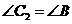 ,
, .
.
所以 ,
,
而
所以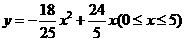
(3) 存在. 当 时,即
时,即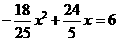
整理,得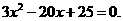 解得,
解得,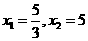 .
.
即当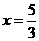 或
或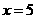 时,重叠部分的面积等于原
时,重叠部分的面积等于原 面积的
面积的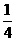
28.(本题满分14分)
在平面直角坐标系xOy中,一次函数y=-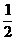 x+5的图象交x轴于点B,与正比例函数
x+5的图象交x轴于点B,与正比例函数
y=kx(k≠0)的图象交于第一象限内的点A.(如图①)
(1)以0、A、B三点为顶点画平行四边形,求这个平行四边形第四个顶点C的坐标;(用含k的代数式表示)
(2)若以0、A、B、C为顶点的平行四边形为矩形,求k的值;(图②备用)
(3)将(2)中的矩形OABC绕点O旋转,使点A落在坐标轴的正半轴上,求所得矩形与原
矩形重叠部分的面积.
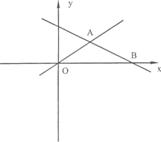
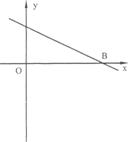
图① 图②
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com