
题目列表(包括答案和解析)
6.
抛物线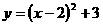 的顶点坐标是
.
的顶点坐标是
.
5.
不等式组 的解集是
.
的解集是
.
4.
若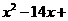
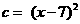 ,则
,则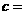 .
.
3.
函数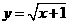 中,自变量x的取值范围是
.
中,自变量x的取值范围是
.
2. 上海已进入老龄化城市,预计到2025年,上海65岁及以上老人将达到
400万人,“400万”用科学记数法可表示为_________.
1.
计算: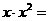 _________.
_________.
13、(2006广东)如图所示,在平面直角坐标中,四边形OABC是等腰梯形,BC∥OA,OA=7,AB=4,∠ COA=60°,点P为x轴上的-个动点,点P不与点0、点A重合.连结CP,过点P作PD交AB于点D.
(1)求点B的坐标;
(2)当点P运动什么位置时,△OCP为等腰三角形,求这时点P的坐标;
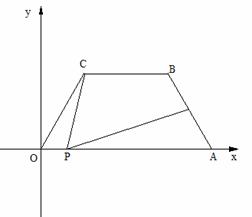 (3)当点P运动什么位置时,使得∠CPD=∠OAB,且
(3)当点P运动什么位置时,使得∠CPD=∠OAB,且 =
=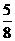 ,求这时点P的坐标。
,求这时点P的坐标。
[解] (1)作BQ⊥x轴于Q.
∵ 四边形ABCD是等腰梯形,
∴∠BAQ=∠COA=60°
在RtΔBQA中,BA=4,
∴BQ=AB·sin∠BAO=4×sin60°=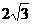
AQ=AB·cos∠BAO=4×cos60°=2,
∴OQ=OA-AQ=7-2=5
∵点B在第一象限内,
∴点B的的坐标为(5, 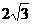 )
)
(2)若ΔOCP为等腰三角形,∵∠COP=60°,
此时ΔOCP为等边三角形或是顶角为120°的等腰三角形
若ΔOCP为等边三角形,OP=OC=PC=4,且点P在x轴的正半轴上,
∴点P的坐标为(4,0)
若ΔOCP是顶角为120°的等腰三角形,则点P在x轴的负半轴上,且OP=OC=4
∴点P的坐标为(-4,0)
∴点P的坐标为(4,0)或(-4,0)
(3)若∠CPD=∠OAB
∵∠CPA=∠OCP+∠COP
而∠OAB=∠COP=60°,
∴∠OCP=∠DPA
此时ΔOCP∽ΔADP
∴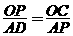
∵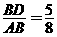
∴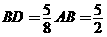 ,
,
AD=AB-BD=4-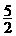 =
=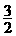
AP=OA-OP=7-OP
∴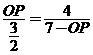
得OP=1或6
∴点P坐标为(1,0)或(6,0).
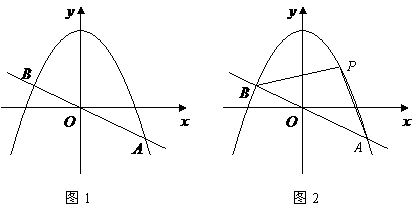
12、(2006湖南长沙)如图1,已知直线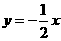 与抛物线
与抛物线 交于
交于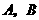 两点.
两点.
(1)求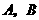 两点的坐标;
两点的坐标;
(2)求线段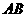 的垂直平分线的解析式;
的垂直平分线的解析式;
(3)如图2,取与线段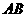 等长的一根橡皮筋,端点分别固定在
等长的一根橡皮筋,端点分别固定在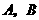 两处.用铅笔拉着这根橡皮筋使笔尖
两处.用铅笔拉着这根橡皮筋使笔尖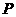 在直线
在直线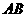 上方的抛物线上移动,动点
上方的抛物线上移动,动点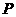 将与
将与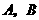 构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时
构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时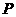 点的坐标;如果不存在,请简要说明理由.
点的坐标;如果不存在,请简要说明理由.
[解]
(1)解:依题意得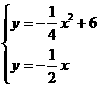 解之得
解之得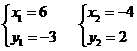
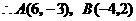
(2)作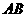 的垂直平分线交
的垂直平分线交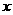 轴,
轴,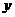 轴于
轴于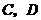 两点,交
两点,交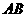 于
于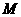 (如图1)
(如图1)
 由(1)可知:
由(1)可知: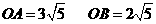
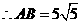
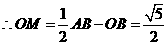
过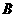 作
作 轴,
轴,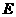 为垂足
为垂足
由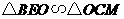 ,得:
,得: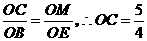 ,
,
同理: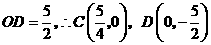
设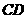 的解析式为
的解析式为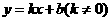
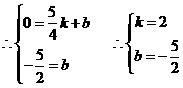
 的垂直平分线的解析式为:
的垂直平分线的解析式为: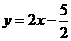 .
.
(3)若存在点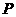 使
使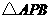 的面积最大,则点
的面积最大,则点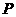 在与直线
在与直线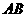 平行且和抛物线只有一个交点的直线
平行且和抛物线只有一个交点的直线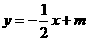 上,并设该直线与
上,并设该直线与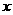 轴,
轴,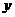 轴交于
轴交于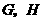 两点(如图2).
两点(如图2).
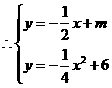
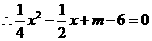
 抛物线与直线只有一个交点,
抛物线与直线只有一个交点,
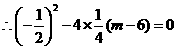 ,
,
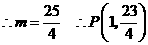
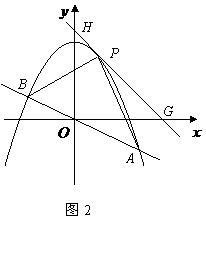 在直线
在直线 中,
中,
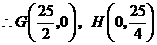
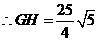
设 到
到 的距离为
的距离为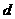 ,
,
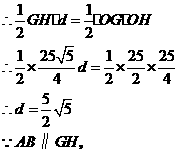
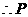 到
到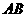 的距离等于
的距离等于 到
到 的距离
的距离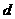 .
.


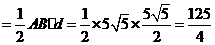 .
.
11、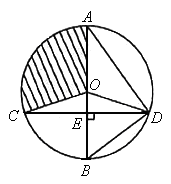 (2006北京海淀)如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。
(2006北京海淀)如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。
(1)若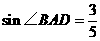 ,求CD的长;
,求CD的长;
(2)若 ∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留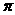 )。
)。
[解]
(1)因为AB是⊙O的直径,OD=5
所以∠ADB=90°,AB=10
在Rt△ABD中,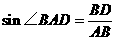
又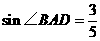 ,所以
,所以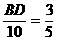 ,所以
,所以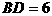
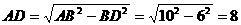
因为∠ADB=90°,AB⊥CD
所以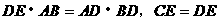
所以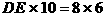
所以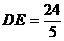
所以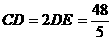
(2)因为AB是⊙O的直径,AB⊥CD
所以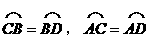
所以∠BAD=∠CDB,∠AOC=∠AOD
因为AO=DO,所以∠BAD=∠ADO
所以∠CDB=∠ADO
设∠ADO=4x,则∠CDB=4x
由∠ADO:∠EDO=4:1,则∠EDO=x
因为∠ADO+∠EDO+∠EDB=90°
所以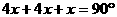
所以x=10°
所以∠AOD=180°-(∠OAD+∠ADO)=100°
所以∠AOC=∠AOD=100°
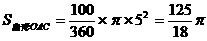
10、(2006湖北宜昌)如图,点O是坐标原点,点A(n,0)是x轴上一动点(n<0=以AO为一边作矩形AOBC,点C在第二象限,且OB=2OA.矩形AOBC绕点A逆时针旋转90o得矩形AGDE.过点A的直线y=kx+m 交y轴于点F,FB=FA.抛物线y=ax2+bx+c过点E、F、G且和直线AF交于点H,过点H作HM⊥x轴,垂足为点M.(1)求k的值;
(2)点A位置改变时,△AMH的面积和矩形AOBC 的面积的比值是否改变?说明你的理由.
[解] (1)根据题意得到:E(3n,0), G(n,-n)
当x=0时,y=kx+m=m,∴点F坐标为(0,m)
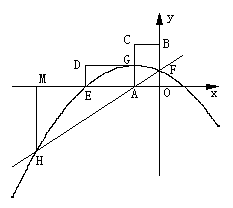 ∵Rt△AOF中,AF2=m2+n2,
∵Rt△AOF中,AF2=m2+n2,
∵FB=AF,
∴m2+n2=(-2n-m)2,
化简得:m=-0.75n,
对于y=kx+m,当x=n时,y=0,
∴0=kn-0.75n,
∴k=0.75
(2)∵抛物线y=ax2+bx+c过点E、F、G,
∴ 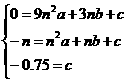
解得:a=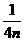 ,b=-
,b=-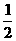 ,c=-0.75n
,c=-0.75n
∴抛物线为y=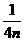 x2-
x2-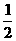 x-0.75n
x-0.75n
解方程组: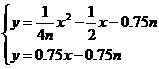
得:x1=5n,y1=3n;x2=0,y2=-0.75n
∴H坐标是:(5n,3n),HM=-3n,AM=n-5n=-4n,
∴△AMH的面积=0.5×HM×AM=6n2;
而矩形AOBC 的面积=2n2,∴△AMH的面积∶矩形AOBC 的面积=3:1,不随着点A的位置的改变而改变.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com