
题目列表(包括答案和解析)
1、(2006重庆)如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成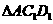 和
和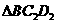 两个三角形(如图2所示).将纸片
两个三角形(如图2所示).将纸片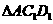 沿直线
沿直线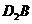 (AB)方向平移(点
(AB)方向平移(点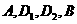 始终在同一直线上),当点
始终在同一直线上),当点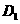 于点B重合时,停止平移.在平移过程中,
于点B重合时,停止平移.在平移过程中,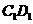 与
与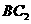 交于点E,
交于点E, 与
与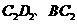 分别交于点F、P.
分别交于点F、P.
(1) 当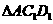 平移到如图3所示的位置时,猜想图中的
平移到如图3所示的位置时,猜想图中的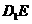 与
与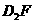 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
(2)
设平移距离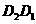 为
为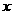 ,
,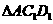 与
与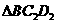 重叠部分面积为
重叠部分面积为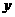 ,请写出
,请写出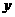 与
与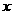 的函数关系式,以及自变量的取值范围;
的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的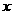 的值,使重叠部分的面积等于原
的值,使重叠部分的面积等于原 面积的
面积的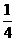 .
.
若存在,求x的值;若不存在,请说明理由.

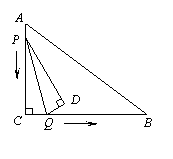 [解] (1)
[解] (1)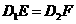 .因为
.因为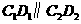 ,所以
,所以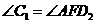 .
.
又因为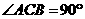 ,CD是斜边上的中线,
,CD是斜边上的中线,
所以,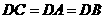 ,即
,即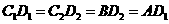
所以,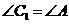 ,所以
,所以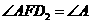
所以,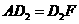 .同理:
.同理: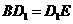 .
.
又因为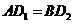 ,所以
,所以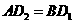 .所以
.所以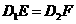
(2)因为在 中,
中,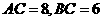 ,所以由勾股定理,得
,所以由勾股定理,得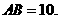
即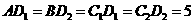
又因为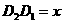 ,所以
,所以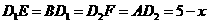 .所以
.所以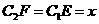
在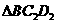 中,
中,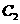 到
到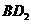 的距离就是
的距离就是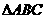 的
的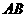 边上的高,为
边上的高,为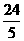 .
.
设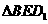 的
的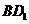 边上的高为
边上的高为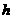 ,由探究,得
,由探究,得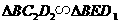 ,所以
,所以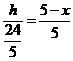 .
.
所以 .
.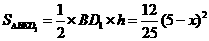
又因为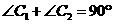 ,所以
,所以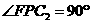 .
.
又因为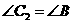 ,
,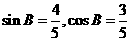 .
.
所以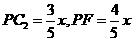 ,
,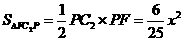
而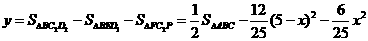
所以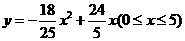
(3) 存在. 当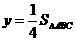 时,即
时,即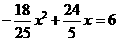
整理,得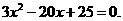 解得,
解得,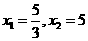 .
.
即当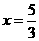 或
或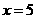 时,重叠部分的面积等于原
时,重叠部分的面积等于原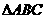 面积的
面积的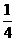
25.抛物线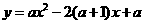 的图像开口向上,与
的图像开口向上,与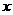 轴交于A、B两点(点A在点B的左边),
轴交于A、B两点(点A在点B的左边),
(1)求证:A、B两点都在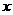 轴的正半轴上;
轴的正半轴上;
(2)已知圆P(点P在第一象限)过A、B两点,且与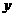 轴相切,
轴相切,
①求圆心P点的坐标;(用含有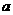 的代数式表示)
的代数式表示)
②当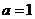 时,圆Q与圆P、
时,圆Q与圆P、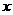 轴、
轴、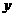 轴都相切,若点Q在第一象限,求满足条件的圆心Q点的坐标.
轴都相切,若点Q在第一象限,求满足条件的圆心Q点的坐标.
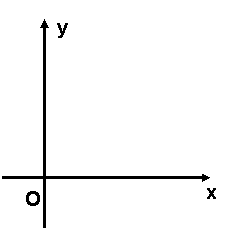
24. 将8个边长为1的正方形拼成如图(1)形状,要求过点P作一条直线l将该图形分割成面积相等的两部分,
将8个边长为1的正方形拼成如图(1)形状,要求过点P作一条直线l将该图形分割成面积相等的两部分,
(1)在图(1)中画出直线l的大致位置;
(2)计算直线l与直线AB所成的夹角(锐角)的正切值.

23.如图△ABC,△CDE都是等边三角形,且点B、C、D在同一直线上,连结AD交CE于点F,连结BE交AC于点G,AD、BE相交于点M,
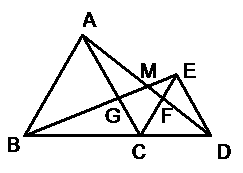 (1)求证:△ABG∽△CDF;
(1)求证:△ABG∽△CDF;
(2)在不添加新的字母和线段的前提下,在图
中再找出2个与△ABG相似的三角形.
22.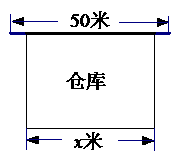 某单位需要建立一个面积为1200平方米的矩形仓库,计划利用一段50米长的旧墙,新墙只围三边,已知每建造1米的新墙需要费用500元,建造顶棚等其它费用为1万元,设当被利用的旧墙长度为
某单位需要建立一个面积为1200平方米的矩形仓库,计划利用一段50米长的旧墙,新墙只围三边,已知每建造1米的新墙需要费用500元,建造顶棚等其它费用为1万元,设当被利用的旧墙长度为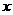 米时,仓库的总建设费用为
米时,仓库的总建设费用为 万元.
万元.
(1)求 关于
关于 的函数解析式及其定义域;
的函数解析式及其定义域;
(2)当建设费用为6万元时,求被利用的旧墙的长度为多少米?
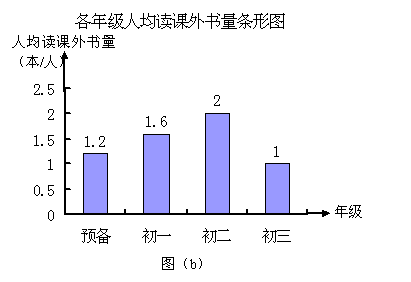
21.某初级中学四个年级学生人数分布如图(a),通过对全体学生寒假期间所读课外书情况调查,制成各年级读课外书情况的条形图,如图(b),已知该校被调查的四个年级共有学生1200人,则
(1)预备年级学生占四个年级总人数的________%;
(2)寒假期间人均读课外书最少的是________年级学生,读课外书总量最少的是________年级学生;
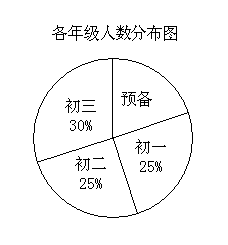 (3)该校四个年级寒假期间人均读课外书________本.
(3)该校四个年级寒假期间人均读课外书________本.
|
20.在直角坐标平面内,把过原点的直线l与双曲线: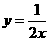 在第一象限的交点记作A,已知A点的横坐标为1,
在第一象限的交点记作A,已知A点的横坐标为1,
(1)求直线l的函数解析式;
(2)将直线l向上平移4个单位后,直线l与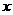 轴、
轴、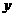 轴分别交于B、C两点,求△BOC的面积.
轴分别交于B、C两点,求△BOC的面积.
19.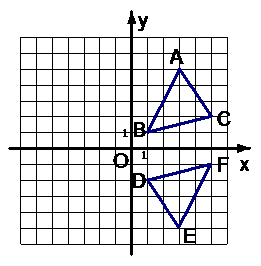 在如图所示的平面直角坐标系中,已知△ABC的顶点坐标都是整数(图中每格的长度为1),请填写下列空格:
在如图所示的平面直角坐标系中,已知△ABC的顶点坐标都是整数(图中每格的长度为1),请填写下列空格:
(1) 点B坐标为_________ .
(2) 若将△ABC沿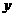 轴翻折得到△A1B1C1,则点B1的坐标为_________,若将
轴翻折得到△A1B1C1,则点B1的坐标为_________,若将
△ABC绕原点O旋转180°得到
△A2B2C2,则点B2的坐标为_________,△A1B1C1与△A2B2C2关于_________轴对称.
(3) 若△ABC与△EFD成中心对称,则对
称中心的坐标为_________.
18.解方程组: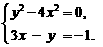
17.先化简,后求值: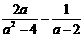 ,其中
,其中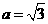 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com