
题目列表(包括答案和解析)
3.要调查某校初三学生周日的睡眠时间,选取调查对象最合适的是( )
A、选取一个班级的学生 B、选取50名男生
C、选取50名女生 D、随机选取50名初三学生
2.下列各式运算正确的是( )
A、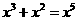 B、
B、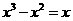 C、
C、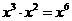 D、
D、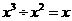
1. 1.计算2-(-3)的结果是
A、-5 B、5 C、-1 D、1
26. (本题满分12分)已知P(m,a)是抛物线y=ax2上的点,且点P在第一象限.
(1)求m的值
(2)直线y=kx+b过点P,交x轴的正半轴于点A,交抛物线于另一点M.
①当b=2a时,∠OPA=90°是否成立?如果成立,请证明;如果不成立,举出一个反例说明;
②当b=4时,记△MOA的面积为S,求 的最大值.
的最大值.
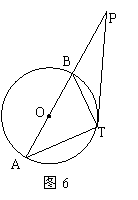
25. (本题满分12分)如图6,点在⊙O的直径AB交TP于P,若PA=18,PT=12,PB=8.
(1)求证:△PTB∽△PAT;
(2)求证:PT为⊙O的切线;
(3)在上是否存在一点C,使得BT2=8TC?若存在,请证明;若不存在,请说明理由.
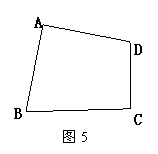
24. (本题满分12分)如图5,在四边形ABCD中,∠A=90°,∠ ABC与∠ADC互补.
(1)求∠C的度数;
(2)若BC>CD且AB=AD,请在图5上画出一条线段,把四边形ABCD分成两部分,使得这两部分能够重新拼成一个正方形,并说明理由;
(3)若CD=6,BC=8,S四边形ABCD=49,求AB的值.
23. (本题满分10分)如图4,学校生物兴趣小组的同学们用围栏围了一个面积为24平方米的矩形饲养场地ABCD.设BC为x米,AB为y米.
(1)求y与x的函数关系式;
(2)延长BC至E,使CE比BC少1米,围成一个新的矩形ABEF,结果场地的面积增加了16平方米,求BC的长.

22. (本题满分10分)如图3,两建筑物的水平距离BC为27米,从点A测得点D的俯
(本题满分10分)如图3,两建筑物的水平距离BC为27米,从点A测得点D的俯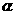 =30°,测得点C的俯角
=30°,测得点C的俯角 =60°,求AB和CD两建筑物的高.
=60°,求AB和CD两建筑物的高.
21. (本题满分8分)2006年3月25日,来自39个国家和地区的运动员参加了厦门国际马拉松赛.图2是本次全程马拉松,半程马拉松,10公里赛程,5公里赛程各项目参赛人数占全体参赛人数比例的扇形统计图.
(1)求参加全程马拉松赛的人数占全体参赛人数的百分比;
(2)已知参加10公里赛程的人数为7200人,求参赛全程马拉松赛的人数.

20. (本题满分9分)如图1,在平行四边形ABCD中,E、F分别是AB、CD上的点,且∠DAF=∠BCE.
(1)求证:△DAF≌△BCE;
 (2)若∠ABC=60°,∠ECB=20°,∠ABC的平分线BN交AF与M,交AD于N,求∠AMN的度数.
(2)若∠ABC=60°,∠ECB=20°,∠ABC的平分线BN交AF与M,交AD于N,求∠AMN的度数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com