
题目列表(包括答案和解析)
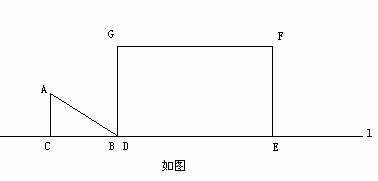
7、如图Rt⊿ABC与矩形DEFG在同一l直线上,∠ACB=900,AC=3cm,AB=5cm,DE=8cm,DF=6cm,现⊿ABC从图(1)位置出发,以1cm/秒的速度向右平移。设运动时间为t秒,重叠部分的面积为Scm2。
(1) 当运动2秒钟时,求重叠部分的面积;(4分)
(2) 是否存在某一时刻,重叠部分的面积不变,若存在,求出持续不变的时间;若不存在,试说明理由;(4分)
(3) 分别求出0≦t≦4,8≦t≦12时的S关于t的函数关系式(6分)
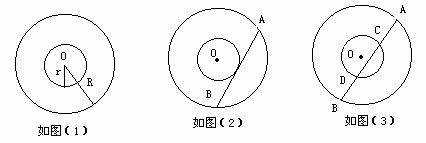
6、在探索图形的面积的时候,王老师带学生们去测量一个环行花坛的面积,学生们想出了多种方法,下面是一段学生的对话:
甲说:如图(1)只要测出大圆和小圆的半径R、r就可以求出环行花坛的面积了;
乙说:如图(2)要找圆心比较麻烦,我只要找一根直棒,让它和小圆相切,再测出它与外圆两交点A、B的长度AB就可以求出环形花坛的面积。
(1)、试用你学习过的知识说明乙同学的理由;
(2)、如图(3)在两同心圆中大圆的弦AB交小圆于C,D两点,已知AB=16cm,DC=7cm,求圆环的面积。(12分)
5、有一个附有进出入管的容器,每单位时间内进出的水量都是一定的,设从某时刻开始的4分钟内只进水,不出水,在随后的8分钟内既进水又出水,得到时间x(分)与水量y(升)之间的关系如图所示.
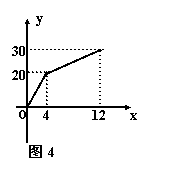 (1)每分钟进水多少?(3分)
(1)每分钟进水多少?(3分)
(2)4≤x≤12时,x与y有何关系?(4分)
(3)若12分钟后只放水,不进水,求y的表达式.(4分)
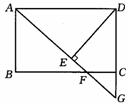
4、如图3,在矩形 ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.根据上述条件,请在图中找出一对全等三角形,并证明你的结论.(10分)
3. 如图:水坝的截面为梯形ABCD,坝顶宽AD=6米,坡面DC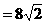 米,AB的坡度为
米,AB的坡度为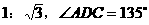 ,
,
求:水坝截面的面积。(10分)
2、解方程:(x+3)(x-1)=5 (8分)
1、计算:2cos30°-(-4)-1+ +
+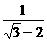 (8分)
(8分)
5、古希腊数学家把数1,3,6,10,15,21,……,叫做三角形数,它有一定的规律性,则第24个三角形数与第22个三角形数的差为
4、某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是 。
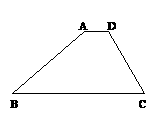
3、已知梯形ABCD中,AD∥BC,AC、BD交于O点,若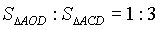 ,则
,则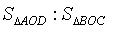 =________。
=________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com