3．(1．10练习第3题)求下列两条平行线的距离：

(1)2x+3y-8=0，　 2x+3y+18=0．

(2)3x+4y=10，　 3x+4y=0．

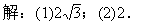
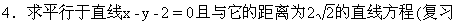
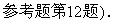
解：x-y-6=0或x-y+2=0．

2．(1．10练习第2题)求下列点到直线的距离：

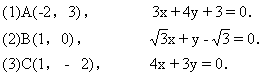
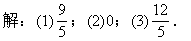
1．(1．10练习第1题)求坐标原点到下列直线的距离：

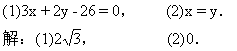
(五)课后小结

(1)点到直线的距离公式及其证明方法．

(2)两平行直线间的距离公式．

(四)例题

例1　 求点P0(-1，2)到直线：(1)2x+y-10=0，(2)3x=2的距离．

解：(1)根据点到直线的距离公式，得

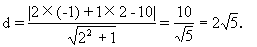
(2)因为直线3x=2平行于y轴，所以

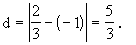
例2　 求平行线2x-7y+8=0和2x-7y-6=0的距离．

解：在直线2x-7y-6=0上任取一点，例如取P(3，0)，则两平行线间的距离就是点P(3，0)到直线2x-7y+8=0的距离(图1-38)．

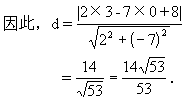
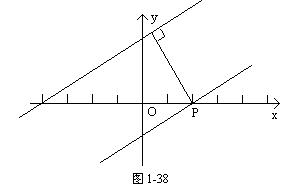
例3　 正方形的中心在C(-1，0)，一条边所在的直线方程是x+3y-5=0，求其它三边所在的直线方程．

解：正方形的边心距

设与x+3y-5=0平行的一边所在的直线方程是x+3y+C1=0，则中心到

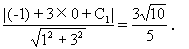
C1=-5(舍去0)或C1=7．

∴与x+3y-5=0平行的边所在的直线方程是x+3y+7=0．

设与x+3y-5=0垂直的边所在的直线方程是3x-y+C2=0，则中心到这

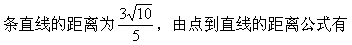
解之有C2=-3或C2=9．

∴与x+3y-5=0垂直的两边所在的直线方程是3x-y-3=0和3x-y+9=0．

(三)推导点到直线的距离公式有思考题4作基础，我们很快得到

设A≠0，B≠0，直线l的倾斜角为α，过点P作PR∥Ox，　 PR与l交于R(x1，x1)(图1-37)．

∵PR∥Ox，

∴y1=y．

代入直线l的方程可得：

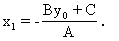
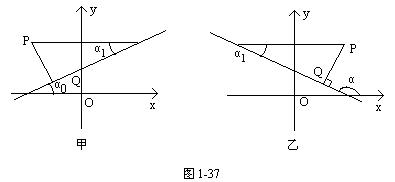
当α＜90°时(如图1-37甲)，α1=α．

当α＞90°时(如图1-37乙)，α1=π-α．

∵α＜90°，

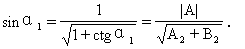
∴|PQ|=|PR|sinα1

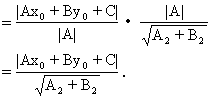
这样，我们就得到平面内一点P(x0，y0)到一条直线Ax+By+C=0的距离公式：

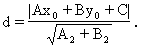
如果A=0或B=0，上面的距离公式仍然成立，但这时不需要利用公式就可以求出距离．

(二)构造特殊的点到直线的距离学生解决

思考题1　 求点P(2，0)到直线L：x-y=0的距离(图1-33)．

学生可能寻求到下面三种解法：

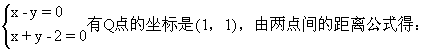
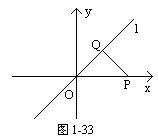
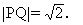
方法2　 设M(x，y)是l：x-y=0上任意一点，则

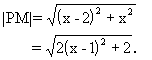
当x=1时|PM|有最小值，这个值就是点P到直线l的距离．

方法3　 直线x-y=0的倾角为45°，在Rt△OPQ中，|PQ|=|OP|

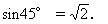
进一步放开思路，开阔眼界，还可有下面的解法：

方法4　 过P作y轴的平行线交l于S，在Rt△PAS中，|PO|=|PS|

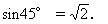
方法5　 过P作x轴的垂线交L于S

∵|OP|·|PS|=|OS|·|PQ|，

比较前面5种解法，以第3种或4种解法为最佳，那么第3种解法是否可以向一般情况推广呢？

思考题2　 求点P(2．0)到直线2x-y=0的距离(图1-34)．

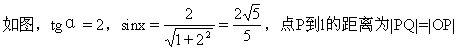
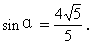
思考题　 3求点P(2，0)到直线2x-y+2=0的距离(图1-35)．

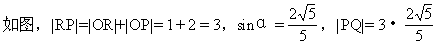
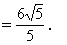
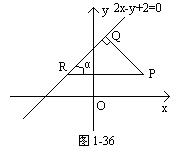
思考题4　 求点P(2，1)到直线2x-y+2=0的距离(图1-36)．

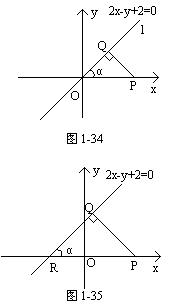
过P作直线的垂线，垂足为Q，过P作x轴的平行线交直线于R，

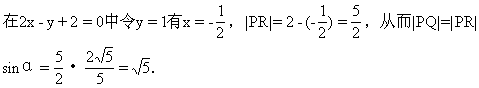
(一)提出问题

已知点P(x0，y0)和直线l：Ax+By+C=0，点的坐标和直线的方程确定后，它们的位置也就确定了，点到直线的距离也是确定的，怎样求点P到直线l的距离呢？

启发、思考，逐步推进，讲练结合．

3．疑点：点到直线的距离公式是在A≠0、B≠0的条件下推得的．事实上，这个公式在A=0或B=0时，也是成立的．