1.利用直角三角形边角之间的关系来解直角三角形,最主要的是记住定义。譬如说,我们要求直角三角形中一个锐角的度数,需根据已知条件是这个角的哪些边来选择函数定义,若已知直角三边形的一个锐角和一边长求另一边长也是如此.

(二)1.了解平面直角坐标系的有关概念,会由点的位置确定点的坐标,会由点的　　　 坐标确定点的位置.

　 2.理解函数的意义,能根据一个具体的函数解析式,确定自变量的取值范围,　 并会由自变量的值求出函数值.

　 3.掌握正比例函数、反比例函数、一次函数、二次函数的概念及性质,会画出　 图象.

　 4.能根据不同条件,用待定系数法求函数解析式.

(一)1.理解锐角三角函数定义,会用锐角三角形定义列出函数关系式解直角三角形.

　 2.了解锐角三角函数的四个同角间的函数恒等式,并会解一些相关的题目.

　 3.理解锐角三角函数的性质,会比较在某个范围内正弦和正弦,正弦和余弦,　 正切和正切,正切和余切的大小,及利用函数值的大小判断角的大小.

　 4.熟记特殊角的三角函数组,并会准确的计算.

　 5.会用解直角三角形的有关知识,解某些实际问题.

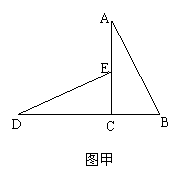
28.如图甲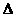：ACB与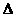DCE是全等的两个直角三角形，其中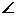ACB=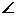DCE=90⁰，AC=4，BC=2，点D、C、B在同一条直线上，点E在边AC上.

(1)直线DE与AB有怎样的位置关系？请证明你的结论；

(2)如图乙：若DCE沿着直线DB向右平移多少距离时，点E恰好落在边AB上，求平移距离DD′^，；

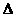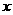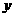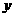(3)在DCE沿着直线DB向右平移的过程中，使DCE与ACB的公共部分是四边形，设平移过程中的平移距离为，这个四边形的面积为，求与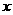的函数关系式，并写出它的定义域.

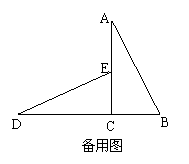
27．如图，已知二次函数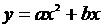的图像开口向下，与x轴的一个交点为B，顶点A在直线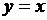上，O为坐标原点。

(1)证明：△AOB是等腰直角三角形；

(2)若△AOB的外接圆C的半径为1，求该二次函数的解析式；

(3)对题(2)中所求出的二次函数，在其图像上是否存在点P(点P与点A不重合)，使得△POC是以PC为腰的等腰三角形，若存在，请求出点P的坐标，若不存在，请说明理由。

26.已知抛物线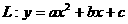(其中a、b、c都不等于0)，它的顶点P的坐标是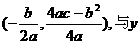轴的交点是M(0，c). 我们称以M为顶点，对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线，直线PM为L的伴随直线.

(1)求抛物线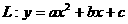(其中a、b、c都不等于0)的伴随抛物线和伴随直

线的解析式；

(2)请直接写出抛物线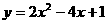的伴随抛物线和伴随直线的解析式：

　　 伴随抛物线的解析式　　　　　　　　　　　　　　　　　　　 ，

　　 伴随直线的解析式　　　　　　　　　　　　　　　　　　　　 ；

(3)若一条抛物线的伴随抛物线和伴随直线分别是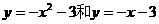，则这条抛物线的解析式是　　　　　　　　　　　　　　　 ；

25.据2006年3月4日的<<解放日报>>报道,上海市就业促进中心发布了本市劳动者职业流

动周期分析报告,该报告说2005年上海劳动者的平均职业流动周期为46.6个月,也就是说平

均每位劳动者在一家单位连续工作近4年.下面是“不同学历劳动者的职业流动周期”与“不

同年龄段劳动者的职业流动周期”的统计图,请根据图中的有关信息回答下列问题:

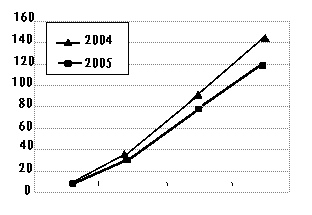
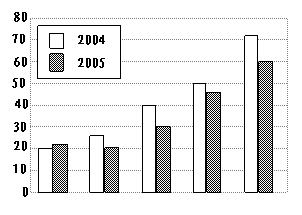
(1)从学历分析来看,2004年不同学历劳动者的职业流动周期的中位数是___________个月,2005年不同学历劳动者的职业流动周期的中位数是________个月,本市劳动者职业流动周期随着学历的增高呈_________趋势(选择“上升”或“下降”);

(2)从年龄分析来看,本市劳动者职业流动周期随着年龄的增大呈_________趋势(选择“上升”或“下降”),2005年的职业流动周期与2004年比较,职业流动的周期_______了(填“缩短”或“延长”), 职业流动周期低于20个月的劳动者年龄范围__________;

(3)本市劳动者,学历为________的职业流动周期最短,年龄范围为_________的职业流动周期最长;

24.2006年3月15日, 深受海内外关注的磁浮铁路沪杭线交通项目获国务院批准.该项目

预计将于2008年建成,建成后,上海至杭州的铁路运行路程将由目前的200千米缩短至175

千米, 磁浮列车的设计速度是现行特快列车速度的3.5倍,运行时间将比目前的特快列车运

行时间约缩短1.2小时,试求磁浮铁路沪杭线磁浮列车的设计速度是每小时多少千米?

23．如图，晚上，小亮在广场上乘凉．图中线段AB表示站立在广场上的小亮，线段PO表示直立在广场上的灯杆，点P表示照明灯．

(1)请你在图中画出小亮在照明灯(P)照射下的影子；

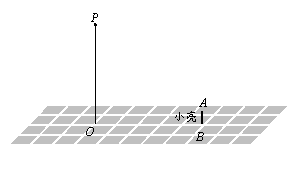(2)如果灯杆高PO＝12m，小亮的身高AB＝1.6m，小亮与灯杆的距离BO＝13m，请求出小亮影子的长度．

22．不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同)，其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为.

(1)试求袋中蓝球的个数.

(2)第一次任意摸一个球(不放回)，第二次再摸一个球，请画树状图或列表格，求两次摸到都是白球的概率.